Cách quy đồng mẫu số và bài tập vận dụng chi tiết

Làm thế nào để quy đồng mẫu số? Khái niệm chung cần nhớ, phương pháp và các dạng bài tập vận dụng về quy đồng mẫu số cực chi tiết.

Trong chương trình của môn Toán lớp 4, quy đồng mẫu số là một trong những kiến thức trọng tâm và phức tạp. Quy đồng mẫu số là quá trình đưa các phân số có mẫu số khác nhau về cùng một mẫu số chung. Việc quy đồng mẫu số giúp chúng ta giải các phép tính và so sánh phân số dễ dàng và chính xác hơn.

Vì vậy trong bài viết này, thayphu sẽ cùng các bạn học sinh tìm hiểu về khái niệm quy đồng mẫu số, các cách quy đồng mẫu và bài tập vận dụng chi tiết để các bạn luyện tập nhé.

Kiến thức chung cần nắm

Mẫu số là gì?

Trong phép tính chia, mẫu số là số ở dưới dấu phân số, mẫu số thường biểu thị cho số lượng phần bằng nhau mà một đại lượng được chia thành. Mẫu số thường được ký hiệu bằng chữ cái "D" hoặc "d".

Ví dụ: phân số ⅞ có mẫu số là 8.

Tử số là gì?

Tử số là số ở trên dấu phân số, tử số thường biểu thị cho số lượng phần được chia. Tử số thường được ký hiệu bằng chữ cái "N" hoặc "n".

Ví dụ: phân số ⅞ có tử số là 7.

Quy đồng mẫu số là gì?

Quy đồng mẫu nghĩa là một mẫu số chung được sử dụng để so sánh hoặc thực hiện các phép tính giữa các phân số có mẫu số khác nhau.

Khi hai hoặc nhiều phân số có mẫu số khác nhau, chúng ta không thể được so sánh hoặc cộng trừ trực tiếp được. Vì vậy, để so sánh hoặc thực hiện các phép tính cộng trừ các phân số một cách dễ dàng, ta cần tìm một mẫu số chung và chuyển đổi các phân số ban đầu sao cho có cùng mẫu số. Nói cách khác thì quy đồng mẫu số giúp ta đưa các phân số về cùng một cấu trúc để thực hiện các phép tính.

Các cách để quy đồng mẫu số

Có 2 dạng toán để quy đồng mẫu của phân số như sau:

Dạng 1: Quy đồng mẫu số khi các mẫu số không chia hết cho nhau.

• Bước 1: Ta tìm bội chung nhỏ nhất (BCNN) của các mẫu số. BCNN là số nhỏ nhất mà tất cả các mẫu số đều chia hết. Sau đó ta chọn BCNN là mẫu số chung của các phân số cần quy đồng.
• Bước 2: Tìm thừa số phụ của từng mẫu số bằng cách chia BCNN cho các mẫu số riêng. Thừa số phụ sẽ là kết quả của phép chia này.
• Bước 3: Nhân cả tử và mẫu của từng phân số với thừa số phụ tương ứng đã tìm ở bước 2. Vậy là ta đã đưa các phân số về cùng một mẫu số chung.

Ví dụ:

Hãy quy đồng mẫu số của các phân số sau: ⅔ và ⅘

• Bước 1: tìm bội chung nhỏ nhất (BCNN) của các mẫu số.

Ta thấy ở đây BCNN (3,5) = 15

Vậy ta chọn 15 làm mẫu số chung.

• Bước 2: Tìm thừa số phụ của từng mẫu số bằng cách chia BCNN cho các mẫu số riêng.

15 : 3 = 5

15 : 5 = 3

• Bước 3: Nhân cả tử và mẫu của từng phân số với thừa số phụ tương ứng.

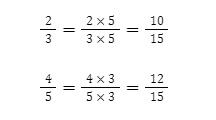
Vậy 10/15 và 12/15 là hai mẫu số sau khi đã quy đồng mẫu số.

Dạng 2: 1 mẫu số chia hết cho số còn lại

Để quy đồng mẫu của hai phân số mà mẫu số phân số thứ nhất chia hết cho mẫu số phân số thứ hai, ta có thể thực hiện các bước sau:

• Bước 1: Xác định mẫu số chung bằng cách lấy mẫu số của phân số thứ hai.
• Bước 2: Tìm thừa số phụ bằng cách chia mẫu số thứ hai cho mẫu số thứ nhất.
• Bước 3: Nhân cả tử và mẫu của phân số thứ nhất với thừa số phụ tìm được ở bước 2.
• Bước 4: Giữ nguyên phân số thứ hai.

Lưu ý: Mẫu số chung được lựa chọn là số tự nhiên nhỏ nhất khác 0 và chia hết cho tất cả các mẫu số ban đầu. Quy đồng mẫu số giúp ta đưa các phân số về cùng một đơn vị để thực hiện các phép tính và so sánh một cách thuận tiện và chính xác.

Ví dụ:

Quy đồng mẫu các phân số 4/5 và 9/10

• Bước 1: Xác định mẫu số chung bằng cách lấy mẫu số của phân số thứ hai.

Ta thấy 10 có thể chia hết cho 5, vậy ta chọn mẫu số chung ở đây là 10.

• Bước 2: Tìm thừa số phụ bằng cách lấy mẫu số thứ hai chia cho mẫu số thứ nhất.

10 : 5 = 2. Vậy thừa số phụ là 2.

• Bước 3: Nhân cả tử và mẫu của phân số thứ nhất với thừa số phụ tìm được ở bước 2.

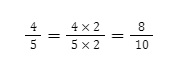
• Bước 4: Giữ nguyên phân số thứ hai.

Vậy ta có 8/10 và 9/10 là 2 phân số sau khi quy đồng mẫu số.

Bài tập

Bài 1: Quy đồng mẫu các phân số sau:

1. ⅗ , ⅔ , 8/9
2. ⅖ và ½
3. 4/7 và ⅓

Gợi ý lời giải:

1. Ta có các phân số: ⅗ , ⅔ , 8/9. Từ đó, ta chọn mẫu số chung là 45 vì 45 là

BCNN của 3, 5 và 9.

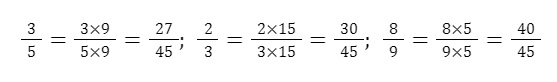
Vậy quy đồng mẫu số các phân số ⅗ , ⅔ , 8/9 ta được 27/45, 30/45, 40/45.

2. Ta có 2 phân số ⅖ và ½. Chọn mẫu số chung là 10 vì 10 là BCNN của 2 và 5.

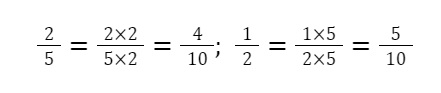
Vậy quy đồng mẫu số 2 phân số ⅖ và ½ ta được 4/10 và 5/10.

3. Ta có phân số 4/7 và ⅓. Chọn mẫu số chung là 21 vì 21 là BCNN của 3 và 7.

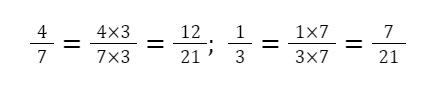
Vậy quy đồng mẫu số 2 phân số 4/7 và ⅓ ta được 12/21 và 7/21.

Bài 2: So sánh các phân số đã cho dưới đây:

1. ⅓ và 4/9
2. ¾ và 5/12
3. ⅗ và 17/30

Gợi ý lời giải:

1. Ta có 2 phân số ⅓ và 4/9. Chọn mẫu số chung là 9.

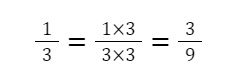
Giữ nguyên phân số 7/9.

Vậy quy đồng mẫu số 2 phân số ⅓ và 7/9 ta được 3/9 và 7/9.

⇔ 3/9 < 7/9 => ⅓ < 7/9

2. Ta có 2 phân số ¾ và 5/12, chọn mẫu số chung là 12.

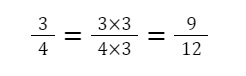
Giữ nguyên phân số 5/12.

Vậy quy đồng mẫu số 2 phân số ¾ và 5/12 ta được 9/12 và 5/12.

⇔ 9/12 > 5/12 => 3/4 > 5/12

3. Ta có phân số ⅗ và 17/30. Chọn mẫu số chung là 30.

Giữ nguyên phân số 17/30.

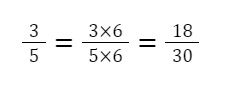
Vậy quy đồng mẫu số ⅗ và 17/30 ta được 18/30 và 17/30.

⇔ 18/30 > 17/30 => 3/5 > 17/30

Kết luận

Qua bài viết trên,các bạn học sinh cũng đã thấy rằng quy đồng mẫu số là một khái niệm quan trọng và hữu ích trong môn toán, đặc biệt là khi giải các bài toán liên quan đến phân số. Việc đưa các phân số về cùng một mẫu số chung giúp chúng ta thực hiện các phép tính và so sánh dễ dàng và chính xác hơn.

Quy đồng mẫu cũng có thể áp dụng trong nhiều lĩnh vực khác nhau, từ giải toán cơ bản trong môn toán tiểu học đến các ứng dụng thực tế trong tài chính, kinh tế và khoa học tự nhiên. Việc hiểu và làm chủ nó sẽ giúp các em giải quyết các vấn đề phức tạp hơn trong cuộc sống hàng ngày. Vì vậy hãy ôn tập và làm bài tập thật tốt để nắm vững kiến thức về quy đồng mẫu nhé.