Cách biểu diễn số hữu tỉ trên trục số cực hay và bài tập

Mỗi số hữu tỉ được biểu diễn bởi 1 điểm trên trục số. Xem ngay cách biểu diễn số hữu tỉ trên trục số đơn giản và dễ hiểu.

Làm thế nào để biết cách biểu diễn số hữu tỉ trên trục số chính xác? Bài viết sau đây sẽ giới thiệu chi tiết các bước và các cách biểu diễn chi tiết nhất. Từ đó giúp các em dễ dàng tư duy, làm tốt bài tập về dạng toán này. Hãy cùng thayphu theo dõi ngay nội dung bên dưới nhé!

Cách biểu diễn số hữu tỉ trên trục số

Để biểu diễn số hữu tỉ trên trục số ta làm theo các bước như sau:

• B1: Viết số hữu tỉ cần biểu diễn dưới dạng phân số tối giản có mẫu số là số dương: a/b (với b > 0)
• B2: Vẽ trục số, chia khoảng có độ dài 1 đơn vị làm b phần bằng nhau, ta có đơn vị mới bằng 1/b đơn vị cũ.
• B3: Số hữu tỉ a/b được biểu diễn bởi 1 điểm A:
  • Trường hợp a > 0 thì điểm A nằm sau (bên phải) gốc O, cách O một đoạn bằng a đơn vị mới.
  • Trường hợp a < 0 thì điểm A nằm trước (bên trái) gốc O, cách O một đoạn bằng a đơn vị mới. Khi đó ta có được vị trí của số hữu tỉ a/b.

Thứ tự trong tập hợp số hữu tỉ

• Trên trục số, nếu a < b thì điểm a nằm trước điểm b
• Trên trục số,các điểm nằm trước gốc O biểu diễn số hữu tỉ âm. Còn các điểm nằm sau gốc O biểu diễn số hữu tỉ dương.
• Số 0 không phải là số hữu tỉ dương, cũng không phải là số hữu tỉ âm.

Để sắp xếp thứ tự các số hữu tỉ ta áp dụng bằng 2 cách như sau:

Đầu tiên là biểu diễn các số hữu tỉ trên trục số

• B1: Biểu diễn các số hữu tỉ trên trục số
• B2: Quan sát trục số
  • Nếu số a nằm trước số b thì a < b
  • Nếu số a và b nằm cùng 1 vị trí thì a = b
  • Nếu số a nằm sau số b thì a > b
• B3: Sắp xếp các số hữu tỉ theo thứ tự đề bài yêu cầu.

Thứ 2 là so sánh các số hữu tỉ

• B1: Viết các số hữu tỉ dưới dạng phân số
• B2: So sánh các phân số ở bước 1
• B3: Sắp xếp các số hữu tỉ theo thứ tự đề bài yêu cầu.

Bài tập vận dụng

Bài tập 1

So sánh 0,5 và 5/2 và hãy cho biết điểm 0,5 nằm trước hay nằm sau điểm 5/2 trên trục số.

Cách giải:

Ta có: 0,5 < 1 và 5/2 = 2,5 > 1 nên 0,5 < 5/2

Vì vậy điểm 0,5 sẽ nằm trước điểm 5/2 trên trục số.

Bài tập 2

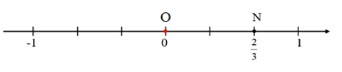
Hãy biểu diễn số hữu tỉ ⅔ trên trục số.

Cách giải:

Để biểu diễn số hữu tỉ ⅔ trên trục số chúng ta thực hiện các bước sau:

• Đầu tiên là vẽ trục số
• Sau đó chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 đến điểm 1) chia thành 3 phần bằng nhau. Từ đó ta được đoạn đơn vị mới bằng ⅓ đơn vị cũ.
• Số hữu tỉ ⅔ được biểu diễn bởi điểm N nằm về phía bên phải gốc O và cách O một đoạn bằng 2 đơn vị mới như hình bên dưới:

Bài tập 3

Hãy sắp xếp các số hữu tỉ sau đây: -1 ½ ; 3/2; -5/2; 7/2 theo thứ tự tăng dần bằng 2 cách (biểu diễn số trên trục số và so sánh)

Cách giải:

Cách 1: Áp dụng cách biểu diễn trên trục số

Vẽ trục số

• Đầu tiên là biểu diễn số -1 1/2

Ta có: -1 ½ = -3/2

Tiến hành chia đoạn thẳng đơn vị (chẳng hạn đoạn từ điểm 0 tới điểm 1) thành 2 phần bằng nhau. Ta sẽ có được đoạn đơn vị mới bằng ½ đơn vị cũ.

Số hữu tỉ -3/2 được biểu diễn bởi điểm A nằm phía trái gốc O và cách gốc O 1 đoạn bằng 3 đơn vị mới (như hình vẽ dưới)

• Thứ 2 là biểu diễn số 3/2

Số hữu tỉ 3/2 sẽ được biểu diễn bởi điểm B nằm phía bên phải của gốc O và cách gốc O 1 đoạn bằng 3 đơn vị mới (như hình vẽ dưới)

Tiếp tục tương tự ta sẽ có các điểm C và D lần lượt biểu diễn cho các số -5/2 và 7/2 (như hình vẽ dưới)

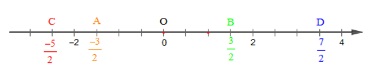
Từ trục số ta thấy rằng vị trí của các điểm từ trái sang phải theo chiều dương lần lượt là các điểm C, A, B, D.

Như vậy thứ tự các số hữu tỉ theo chiều tăng dần sẽ là -5/2; -1 ½ ; 3/2; 7/2.

Cách 2: Áp dụng so sánh

Ta có: -1 ½ = -3/2

Bởi vì - 5 < -3 < 3 < 7 nên -5/2 < - 3/2 < 3/2 < 7/2

Như vậy sắp xếp các số hữu tỉ theo thứ tăng dần là -5/2; -1 ½ ; 3/2; 7/2.

Bài tập tự luyện

Bài 1: Số nào sau đây biểu diễn số hữu tỉ < -7/13?

1. 7/13
2. 7/-13
3. 14/-13
4. 14/-36

Bài 2: Phân số nào sau đây không biểu diễn số hữu tỉ -2/9?

1. -4/18
2. 2/-9
3. 6/ -27
4. 8/36

Bài 3: Cho các phân số sau: ½; 12/28; 6/21; -30/ -70; 15/-35; 7/3; -3/7

Hỏi có bao nhiêu phân số biểu diễn số hữu tỉ 3/7?

1. 1
2. 2
3. 6
4. 7

Bài 4: Cho 2 điểm M, N lần lượt biểu diễn các số hữu tỉ 3/2 và -3/2 như hình vẽ bên dưới:

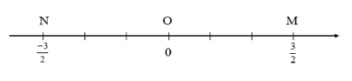
Kết luận nào sau đây là đúng?

1. OM > ON
2. OM = ON
3. OM < ON
4. OM = -ON

Bài 5: Trong 4 điểm A, B, C, D trên trục số bên dưới có 1 điểm biểu diễn số hữu tỉ -4/3. Hãy tìm điểm đó?

1. Điểm A
2. Điểm B
3. Điểm C
4. Điểm D

Vừa rồi là cách biểu diễn số hữu tỉ trên trục số và các bài tập thực hành chi tiết. Chúc các em có những phút giây học tập hiệu quả và làm tốt các đề thi nhé! Đừng quên theo dõi kênh thường xuyên để cập nhật những bài học thật hay!