Bán kính hình tròn, công thức tính chuẩn và bài tập áp dụng

Bán kính hình tròn là đoạn thẳng nối tâm hình tròn với một điểm bất kỳ trên đường tròn. Công thức tính và bài tập vận dụng chi tiết của bán kính hình tròn.

Trong toán học, hình tròn hay bán kính hình tròn cũng là những khái niệm cơ bản trong hình học, đóng vai trò quan trọng trong việc tính toán các đại lượng khác của hình tròn như chu vi, diện tích.

Trong bài viết này, thayphu sẽ cùng các bạn tìm hiểu về bán kính hình tròn như định nghĩa, tính chất, công thức tính và ứng dụng của chúng trong cuộc sống nhé.

Bán kính hình tròn là gì?

Hình tròn là một hình học đặc biệt được tạo thành bởi tập hợp các điểm trong mặt phẳng, cách nhau một khoảng cách nhất định từ một điểm gọi là tâm. Tất cả các điểm trên mặt phẳng có cùng khoảng cách đến tâm đều thuộc vào hình tròn.

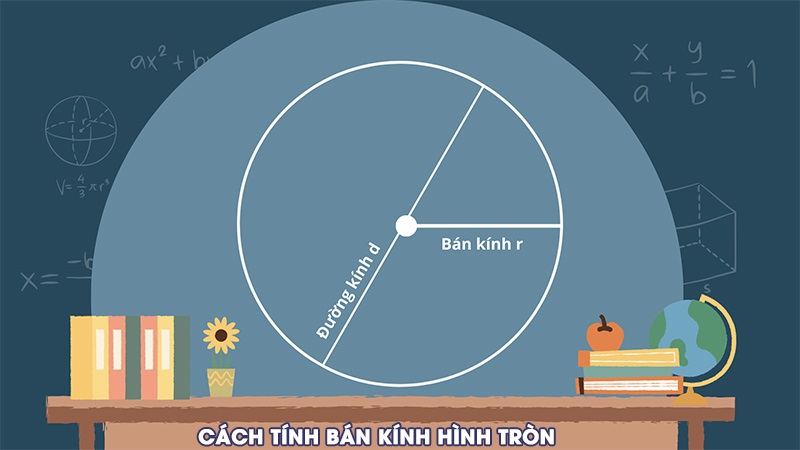
Bán kính hình tròn là đoạn thẳng nối tâm hình tròn với một điểm bất kỳ trên đường tròn.

Hay nói cách khác, bán kính của một hình tròn là đường kính chia cho 2. Đường kính là một đoạn thẳng đi qua tâm của hình tròn và có hai điểm tiếp xúc với cạnh của hình tròn.

Ký hiệu của bán kính thường là r hoặc R.

Các tính chất cần lưu ý của bán kính hình tròn

• Bán kính luôn lớn hơn 0.
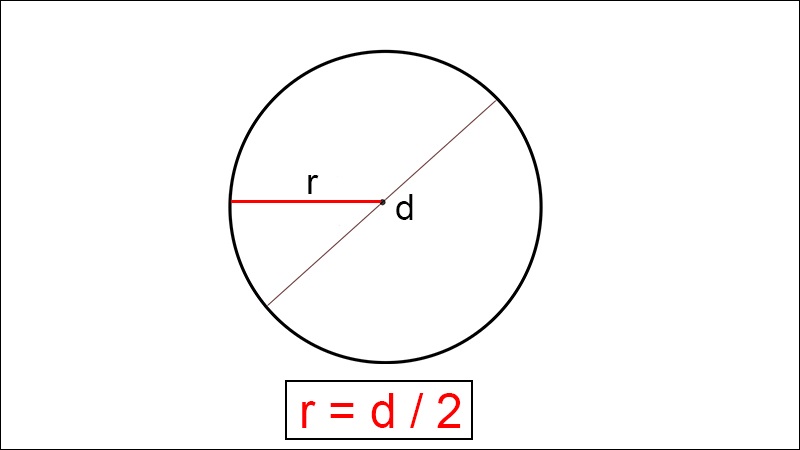
• Bán kính và đường kính có mối quan hệ tỷ lệ nghịch với nhau: r = d/2.
• Giá trị của số π (pi) xấp xỉ 3,14159.

Công thức tính bán kính hình tròn

Từ đường kính (d): r = d/2

Như ta đã biết ở phần định nghĩa, bán kính sẽ bằng ½ đường kính hay đường kính gấp 2 lần bán kính.

Ta có công thức như sau:

d = 2r ⇒ r = d/2

Trong đó: d là đường kính, r là bán kính.

Ví dụ: Cho một chiếc đĩa hình tròn, biết đường kính của chiếc đĩa là 20cm, hãy tính bán kính của nó.

Ta có đường kính của chiếc đĩa: d = 20cm

Suy ra bán kính của chiếc đĩa là: r = d/2 = 20/2 = 10cm

Vậy bán kính của chiếc đĩa đã cho là 10 cm.

Từ chu vi (C): r = C / (2π)

Nếu ta không biết được đường kính mà chỉ biết chu vi của hình tròn. Vậy làm thế nào để tính bán kính hình tròn?

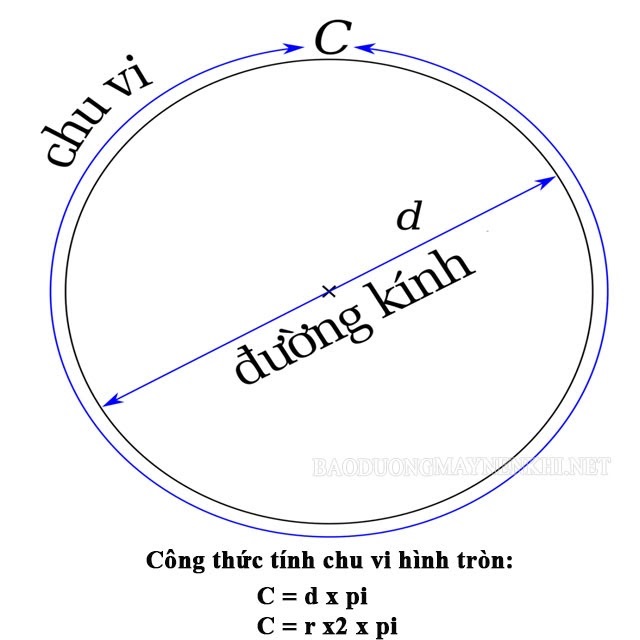
Ta có công thức tính chu vi của hình tròn là:

C = d x π = 2r x π

⇒ r = C/ 2π

Trong đó: C là chu vi hình tròn, d là đường kính, r là bán kính, π bằng xấp xỉ 3,14.

Ví dụ: Cho hình tròn có chu vi là 31,4 cm,hãy tính bán kính hình tròn đã cho.

Ta có chu vi hình tròn là C = 31,4 cm.

Suy ra bán kính hình tròn là: r = C/ 2π = 31,4/ (2 x 3,14) = 5

Vậy bán kính đường tròn đã cho là 5 cm.

Từ diện tích (S): r = √(S/π)

Tương tự như chu vi hình tròn, nếu ta không biết được đường kính mà chỉ biết diện tích của hình tròn. Vậy làm thế nào để tính bán kính hình tròn?

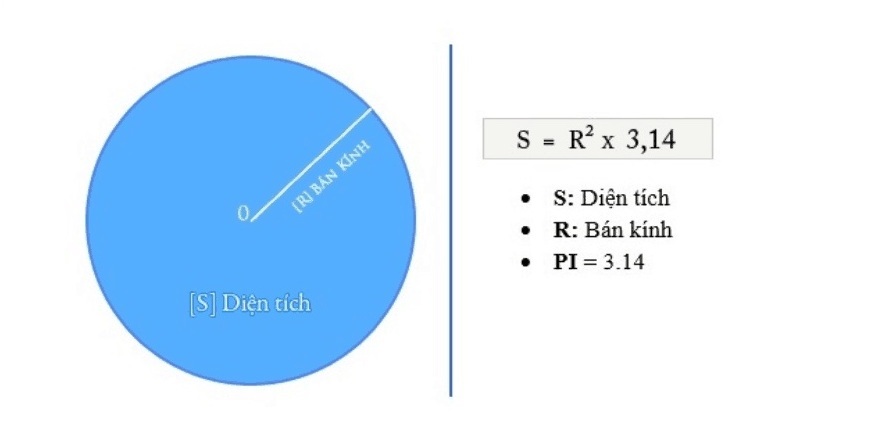
Ta có công thức tính diện tích của hình tròn là:

S = 2rπ = r x 2 x 3.14

⇒ r = √(S/π)

Trong đó: S là diện tích hình tròn, d là bán kính, π bằng xấp xỉ 3,14.

Ví dụ: Một chiếc lốp xe tải có diện tích là 188,4 cm². Hãy tính bán kính của chiếc lốp xe tải trên.

Ta có diện tích của lốp xe tải là S = 188,4 cm².

Suy ra bán kính của lốp xe là: r = √(S/π) = √(188,4/ 3,14) = 30 cm

Vậy bán kính của lốp xe tải đã cho là 30 cm.

Ứng dụng

• Diện tích hình tròn: Bán kính của một hình tròn được sử dụng để tính diện tích của nó. Diện tích hình tròn được tính bằng công thức A = πr^2, trong đó A là diện tích và r là bán kính. Ví dụ, khi biết bán kính của một hồ nước hoặc một vòng tròn trên một bề mặt, ta có thể tính diện tích của nó.
• Chu vi hình tròn: Bán kính của một hình tròn cũng được sử dụng để tính chu vi của nó. Chu vi của hình tròn được tính bằng công thức C = 2πr, trong đó C là chu vi và r là bán kính. Ví dụ, khi biết bán kính của một vòng tròn đường kính hoặc một đường tròn trên một bề mặt, ta có thể tính chu vi của nó.
• Tính toán trong hình học: Bán kính của hình tròn được sử dụng để giải quyết các bài toán hình học phức tạp. Ví dụ, bán kính hình tròn ngoại tiếp được sử dụng để xác định các đường tròn và hình tròn nội tiếp, tính khoảng cách giữa các đường tròn, và giải các bài toán tương tự.
• Thiết kế và kiến trúc: Bán kính của hình tròn được sử dụng trong thiết kế và kiến trúc để xác định kích thước, tỷ lệ và vị trí của các yếu tố hình học. Ví dụ, bán kính của một vòng tròn trong một kết cấu xây dựng có thể được sử dụng để xác định kích thước của các cột, cầu thang, đường cung của cửa sổ và các yếu tố khác.
• Công nghệ và khoa học: Bán kính của hình tròn được sử dụng trong nhiều lĩnh vực công nghệ và khoa học, bao gồm công nghệ thông tin, điện tử, vật liệu, quang học, và các lĩnh vực khác. Ví dụ, bán kính quang học của một ống kính quang học quyết định các thuộc tính quang học như tiêu cự và độ phân giải.

Bài tập vận dụng

Bài tập 1: Đoạn thẳng OC ở hình dưới đây gọi là gì?

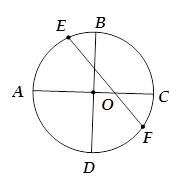
A. Đường kính

B. Bán kính

C. Tâm đường tròn

D. Chu vi

Đáp án: B. Bán kính.

Bài tập 2: Đâu là bán kính của hình tròn tâm O như hình dưới đây?

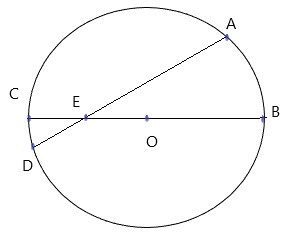
A. DE

B. AE

C. OB

D. BC

Đáp án: C. OB.

Bài tập 3: Một hình tròn tâm O có đường kính AB bằng 16cm. Vậy bán kính của hình tròn tâm O là:

A. 8 cm

B. 16 cm

C. 32 cm

d. 8π cm

Đáp án: A. 8 cm.

Bài tập 4: Cho ba hình tròn như hình vẽ minh họa dưới đây, mỗi hình tròn đều có bán kính là 12 km. Chú ong bay đi lấy mật từ điểm A đến điểm C theo đường gấp khúc ABC. Vậy chú ong đã bay quãng đường bao nhiêu km?

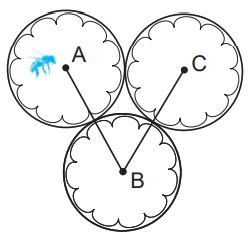
Lời giải:

Quan sát hình minh họa và đề bài, ta thấy rằng đoạn thẳng AB và BC đều có độ dài bằng 2 lần bán kính của hình tròn

Suy ra AB = BC = 2 x 12 = 24 km

Độ dài đoạn đường gấp khúc ABC là:

AB + BC = 24 + 24 = 48 km

Vậy chú ong đã bay một quãng đường là 48 km.

Kết luận

Qua bài viết trên, ta đã thấy rằng bán kính hình tròn là một dạng toán đơn giản và rất thú vị. Ngoài ra, nó còn có rất nhiều ứng dụng hữu ích trong cuộc sống. Đây là một dạng toán tuy đơn giản nhưng đóng vai trò rất quan trọng bởi nó là nền tảng để có thể xây nên những bức tường kiến thức cho sau này. Vì vậy các bạn học sinh hãy thường xuyên ôn luyện và chăm chỉ giải bài tập để nắm vững nền tảng kiến thức này nhé.