Phân số thập phân là gì? Ứng dụng và các dạng bài tập cụ thể

Làm thế nào để biểu diễn một phân số thập phân? Định nghĩa, ứng dụng và các dạng bài tập cụ thể của dạng toán này như so sánh, biến đổi phân số…

Phân số thập phân là một khái niệm cơ bản và quan trọng trong toán học, đặc biệt là trong chương trình Toán lớp 5. Nó là một phần của số học cơ bản và có ứng dụng rộng rãi trong cuộc sống hàng ngày. Phân số thập phân được coi là một khái niệm quan trọng bởi nó biểu diễn các giá trị trung gian chính xác hơn so với số nguyên.

Vì vậy trong bài viết này, hãy cùng thayphu khám phá về phân số thập phân, định nghĩa, ứng dụng và các dạng bài tập cụ thể của chúng nhé.

Phân số thập phân là gì?

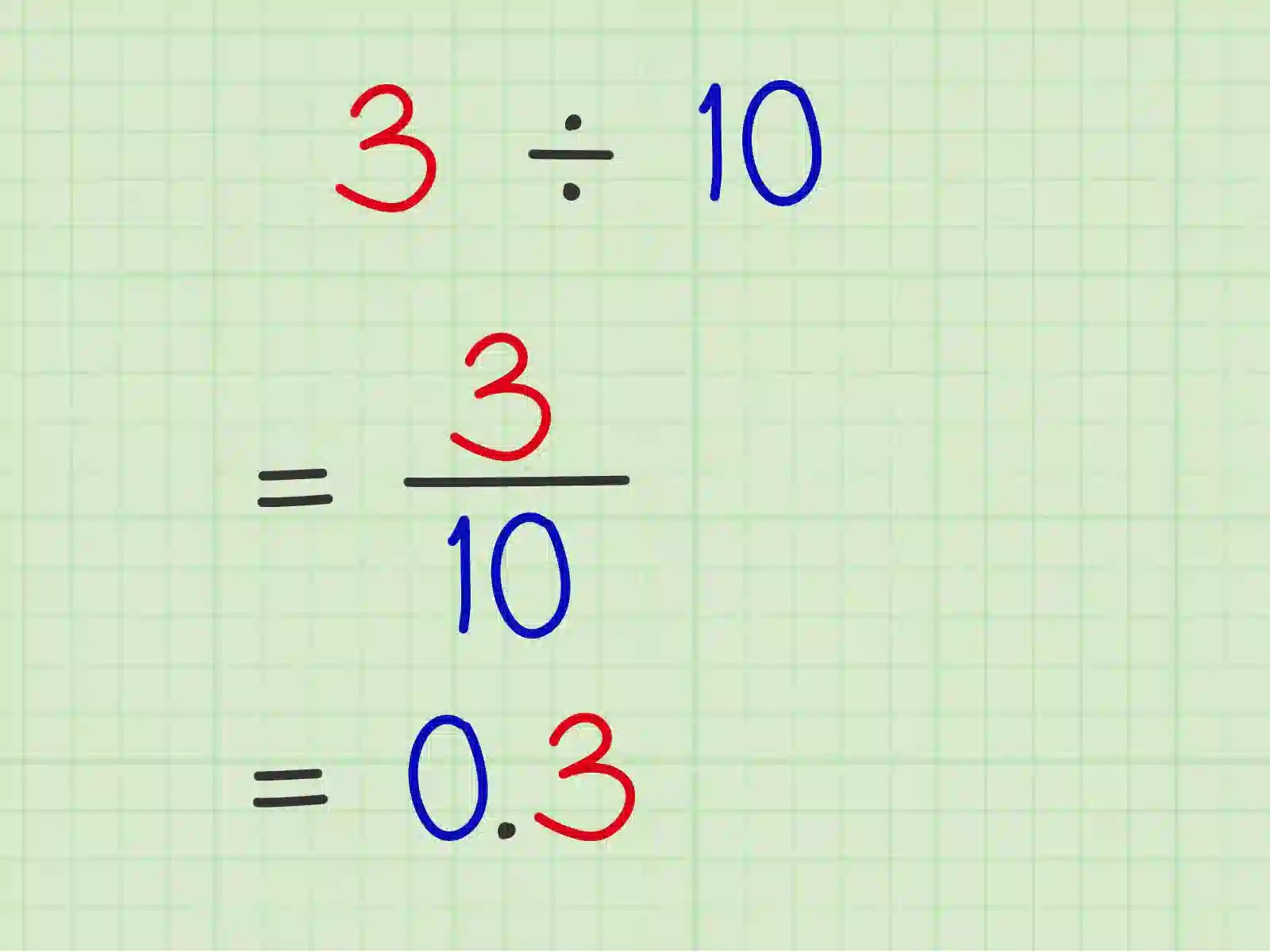
Phân số thập phân là phân số mà tử số (dòng trên) là một số nguyên hoặc thập phân và mẫu số (dòng dưới) là một số nguyên lớn hơn 0.

Phân số thập phân được sử dụng để biểu diễn các giá trị nằm giữa các số nguyên, cho phép chúng ta đo lường và diễn giải các phần phần tử của một đơn vị hoặc một tập hợp.

Trong phân số thập phân, mẫu số thường là một lũy thừa của 10, ví dụ như 10, 100, 1000,... và tử số là một số nguyên hoặc một số thập phân. Tử số biểu thị phần của một đơn vị hoặc một tập hợp, trong khi mẫu số xác định độ chính xác của phần đó.

Ví dụ: Phân số thập phân 0.5 có tử số là 5 và mẫu số là 10, do đó nó có thể được viết dưới dạng phân số 5/10. Tuy nhiên, chúng ta thường đơn giản hóa phân số này bằng cách rút gọn nó thành 1/2.

Ứng dụng của phân số thập phân trong đời sống

• Tiền tệ: Phân số thập phân được sử dụng để biểu diễn các đơn vị tiền tệ và tỷ giá hối đoái. Ví dụ, 1 đô la Mỹ có thể được biểu diễn dưới dạng 1.00 USD.
• Thời gian: Nó cũng được sử dụng để biểu diễn thời gian trong các đơn vị như giờ, phút và giây. Ví dụ, 2.5 giờ có nghĩa là 2 giờ 30 phút.
• Tỉ lệ phần trăm: Chúng ta sử dụng phân số thập phân để biểu diễn tỷ lệ phần trăm trong các khía cạnh như giảm giá, lợi suất và tăng trưởng. Ví dụ, một sản phẩm được giảm giá 20% có thể được biểu diễn dưới dạng phân số thập phân là 0.2.
• Đo lường: Trong các đơn vị đo lường như mét, kilogram, lít, phân số thập phân được sử dụng để biểu diễn các giá trị chính xác hơn. Ví dụ, 1.5 mét có nghĩa là 1 mét 50 centimet.
• Tỷ lệ và phần trăm trong thống kê: Phân số thập phân được sử dụng để biểu diễn tỷ lệ và phần trăm trong các dữ liệu thống kê. Ví dụ, 25% có thể được biểu diễn dưới dạng phân số thập phân là 0.25.

Các dạng bài tập về phân số thập phân

Dạng 1: So sánh hai số thập phân

Phương pháp giải: Để so sánh hai phân số thập phân, ta chỉ cần so sánh chúng như các phân số bình thường.

Ví dụ: Điền dấu < hoặc > vào chỗ chấm:

1. 3/10 … 2/10

So sánh 2 số trên, ta thấy cả 2 phân số đều có mẫu chung là 10.

Mà 3 > 2 nên 3/10 > 2/10.

2. 700/1000 … 80/100

700/1000 có phân số dạng rút gọn là 7/10

80/100 có phân số dạng rút gọn là 8/10

Cả 2 phân số đều trở về dạng có cùng mẫu số là 10.

Mà 7 < 8 nên 700/1000 < 80/100.

Dạng 2: Đọc, viết các phân số thập phân

Phương pháp giải: Cách đọc và viết các phân số thập phân cũng tương tự như các phân số bình thường.

Muốn đọc một phân số, ta đọc phần tử số trước, đọc chữ “phần” rồi đọc mẫu số.

Muốn viết một phân số, tử số là số ở trên dấu gạch ngang, mẫu số là số dưới dấu gạch và mẫu số phải khác 0.

Ví dụ:

Phân số 4/10 đọc là bốn phần mười.

Phân số 7/100 đọc là bảy phần trăm.

Phân số hai tám phần trăm viết là 28/100.

Dạng 3: Đổi một phân số thường thành một phân số thập phân

Phương pháp giải:

• Tìm 1 số sao cho số đó nhân (hoặc chia) với mẫu số ta được kết quả là 10, 100, 1000.
• Nhân (hoặc chia) cả tử số và mẫu số của phân số cần đổi với số đó.

Ví dụ: Đổi các phân số sau thành dạng phân số thập phân: 2/5, 48/600, 4/25.

Quan sát mẫu số của các phân số đã cho, ta thấy:

2 x 5 = 10; 600 : 6 = 100; 25 x 4 = 100

Vậy ta có thể biến đổi các phân số thành phân số thập phân như sau:

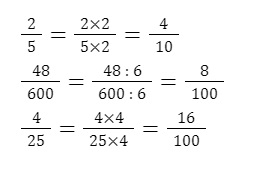
Kết luận

Qua bài viết trên, thayphu.net hy vọng các bạn đã nắm được các khái niệm cơ bản, ứng dụng và các dạng bài tập của phân số thập phân bởi lẽ, phân số thập phân là một khái niệm cơ bản và quan trọng trong toán học, và có ứng dụng rộng rãi trong nhiều lĩnh vực trong cuộc sống hàng ngày. Đây được coi là một trong các khái niệm nền tảng của chương trình toán lớp 5, vì vậy các bạn hãy ôn luyện nó thật kỹ để có thể áp dụng chúng để giải các dạng toán nâng cao hơn nữa nhé.