Hỗn số là gì? Cách chuyển đổi và các phép tính cơ bản

Như thế nào là hỗn số? Làm thế nào để biểu diễn một giá trị ở dạng hỗn số? Cách chuyển đổi hỗn số sang các dạng khác nhau và các phép tính cơ bản của chúng.

Hỗn số là một khái niệm tuy đơn giản nhưng cũng rất quan trọng trong toán học. Về cơ bản, hỗn số bao gồm một phần nguyên và một phân số. Vì vậy mà nó được sử dụng để biểu diễn các giá trị nằm giữa các số nguyên.

Trong bài viết này, thayphu sẽ giúp các bạn hiểu rõ hơn về định nghĩa của hỗn số, các cách chuyển đổi và các phép tính cơ bản của chúng nhé.

Kiến thức chung cần nắm về hỗn số

Hỗn số là gì?

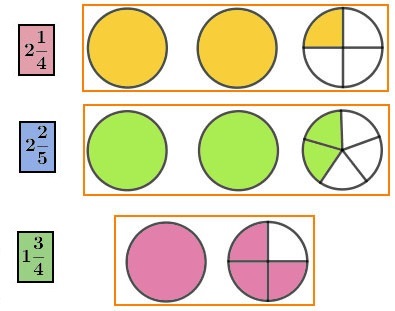
Hỗn số là một dạng biểu diễn số học gồm một phần số nguyên và một phần phân số. Nó được biểu diễn dưới dạng a b/c (hoặc a + b/c), trong đó a là phần nguyên, b là tử số của phân số và c là mẫu số của phân số. Phần nguyên a là một số nguyên không âm, và phân số b/c là một phân số dương.

Ví dụ, trong hỗn số 3 ½ (hoặc 3 + ½), số nguyên a là 3, tử số b là 1 và mẫu số c là 2. Hỗn số này có thể được hiểu là "ba rưỡi".

Cách đọc và viết hỗn số chuẩn

Cách đọc và viết hỗn số khá đơn giản. Hỗn số được cấu tạo từ một phần số nguyên và một phần phân số, và phần số nguyên được đặt trước phần phân số.

• Để đọc hỗn số 1 cách chính xác, ta đọc giá trị phần nguyên rồi đến phần phân số.

Ví dụ: 3 ½ đọc là ba một phần hai.

• Tương tự như cách đọc, ta cũng trình bày hỗn số theo thứ tự phần nguyên rồi đến phần phân số.

Ví dụ: phân số 9/4 có phần nguyên là 2 và phần phân số là ¼. Vậy ta viết phân số theo dạng hỗn số là 2 ¼.

Các cách chuyển đổi hỗn số

Kiến thức về chuyển đổi hỗn số thành các dạng khác nhau là 1 kiến thức cơ bản. Từ dạng hỗn số, ta có thể chuyển nó thành dạng phân số, số thập phân và ngược lại.

Từ phân số sang hỗn số

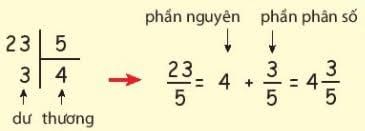
Muốn chuyển một phân số thành dạng hỗn số, ta cần xác định tử số và mẫu số của phân số đó. Lưu ý nếu tử số lớn hơn mẫu số thì có thể thực hiện phép tính. Nhưng nếu tử số bằng hoặc nhỏ hơn mẫu số thì không thể chuyển đổi phân số sang hỗn số.

• Bước 1: Chia tử số cho mẫu số để tìm phần nguyên.
• Bước 2: Lấy phần dư sau khi chia tử số cho mẫu số để tạo phân số mới.
• Bước 3: Rút gọn phân số mới nếu cần thiết và kết luận.

Ví dụ: Chuyển đổi phân số 5/2 sang hỗn số:

• Bước 1: 5 ÷ 2 = 2 (phần nguyên) và dư 1
• Bước 2: Phân số mới là ½
• Bước 3: Kết quả chuyển đổi là hỗn số 2 ½.

Từ hỗn số sang phân số

Ta có hỗn số cần chuyển đổi có dạng a b/c.

• Bước 1: Ta nhân phần nguyên a với mẫu số c và cộng tử số b để tính tổng các phần tử của phân số.

Công thức: a x c + b

• Bước 2: Kết quả thu được là tổng của tử số và mẫu số mới. Ta đặt tử số là tổng và giữ nguyên mẫu số.
• Bước 3: Rút gọn phân số mới nếu cần thiết và kết luận.

Ví dụ: Chuyển đổi hỗn số 3 ½ sang dạng phân số

• Bước 1: 3 x 2 + 1 = 7 (tổng tử số mới)
• Bước 2: Phân số mới là 7/2
• Bước 3: Phân số 7/2 không thể rút gọn được, vậy nên kết quả chuyển đổi là 7/2.

Từ hỗn số sang số thập phân

Ta có thể thực hiện theo 2 cách như sau:

Cách 1:

• Ta đổi hỗn số sang phân số.
• Lấy tử số chia cho mẫu số của phân số đó, ta sẽ thu được một số thập phân.

Cách 2:

• Giữ nguyên phần nguyên của hỗn số đã cho. Trong phần phân số, ta lấy tử số chia cho mẫu số.
• Sau đó lấy kết quả của phép chia cộng với phần nguyên của hỗn số ban đầu. Từ đó ta sẽ thu được một số thập phân.

Ví dụ: Đổi hỗn số 5 ½ sang dạng số thập phân.

Ta giữ phần nguyên 5 của hỗn số, rồi thực hiện phép chia 1/2 ta được 0,5.

Vậy 5 ½ ở dạng số thập phân là 5 + 0,5 = 5,5.

Các phép tính của hỗn số

Phép tính cộng và trừ hỗn số

Phương pháp: Để thực hiện phép tính cộng trừ các hỗn số, phương pháp đơn giản nhất đó là ta chuyển các hỗn số sang dạng phân số. Rồi thực hiện phép cộng trừ hoặc quy đồng mẫu số của phân số.

Ví dụ: Thực hiện phép cộng các hỗn số sau:

1 ¾ + 2 ½

= 7/4 + 5/2

Quy đồng mẫu số 2 phân số ta được:

= 7/4 + 10/4 = 17/4 = 4 ¼

Vậy 1 ¾ + 2 ½ = 4 ¼

Phép tính nhân và chia hỗn số

Phương pháp: Tương tự như các phép tính cộng trừ hỗn số, cách dễ nhất để thực hiện các phép tính nhân chia hỗn số đó là chuyển hỗn số về dạng phân số rồi thực hiện các phép tính nhân chia phân số.

Ví dụ: Nhân các hỗn số sau:

2 ⅓ x 3 ¼

= 7/3 x 13/4

= 91/12 = 7 7/12.

Vậy 2 ⅓ x 3 ¼ = 7 7/12.

Các ứng dụng của hỗn số

Hỗn số được sử dụng rất nhiều trong toán học và các lĩnh vực khác. Sau đây là một vài ứng dụng tiêu biểu của hỗn số để chúng ta có thể sử dụng chúng trong đời sống:

• Biểu diễn số thập phân: Hỗn số có thể được sử dụng để biểu diễn một số thập phân không chuẩn hoặc số thập phân lặp, giúp cho con số bớt phức tạp hơn. Ví dụ, 1 1/3 có thể biểu diễn 1.3333... trong số thập phân.
• Phân loại và so sánh: Hỗn số được sử dụng để phân loại và so sánh các giá trị nằm giữa các số nguyên. Ví dụ như ta có thể so sánh các hỗn số để xác định chúng lớn hơn, nhỏ hơn hoặc bằng nhau.
• Giải quyết bài toán: Hỗn số được sử dụng để giải quyết các bài toán liên quan đến phân phối, tỷ lệ, tổng hợp và phân tích dữ liệu.

Ví dụ về hỗn số trong 1 bài toán thực tế như sau:

Trong một cuộc đua, vận động viên A chạy được 3/4 vòng trong thời gian 2 phút. Hỏi vận động viên A đã chạy trong bao lâu để hoàn thành một vòng đua?

Gợi ý lời giải:

Để giải bài toán này, ta có thể sử dụng hỗn số.

Đặt x là thời gian cần để hoàn thành một vòng đua. Vận động viên A đã chạy được 3/4 vòng trong 2 phút. Vậy ta có:

¾ . x = 2

⇔ x = 2 . 4/3 = 8/3

Vậy, vận động viên A cần khoảng 8/3 (hay 2 ⅔) phút để hoàn thành một vòng đua.

Kết luận

Hỗn số là một khái niệm khá thú vị và quan trọng trong toán học, đặc biệt là trong chương trình toán bậc tiểu học. Ngoài ra, nó có ứng dụng trong nhiều bài toán thực tế. Qua bài viết này, thayphu.net đã giới thiệu đến các bạn định nghĩa về hỗn số, cách chuyển đổi và các phép tính của hỗn số. Đồng thời cũng có rất nhiều ví dụ minh họa cụ thể để các bạn có thể dễ hiểu hơn.

Hi vọng sẽ giúp các bạn học sinh nắm rõ hơn về hỗn số và có thể áp dụng chúng để giải các dạng toán lớp 5 nâng cao hơn nhé.