So sánh hỗn số, phương pháp và quy tắc khi so sánh

Làm thế nào để so sánh hai hỗn số? Các phương pháp để so sánh hỗn số, quy tắc cần nắm khi so sánh và bài tập vận dụng về hỗn số.

Trong toán học, hỗn số đóng một vai trò quan trọng trong việc so sánh các giá trị không đầy đủ. So sánh hỗn số cho chúng ta cái nhìn tổng quan về mối quan hệ giữa các giá trị và giúp chúng ta rút ra kết luận một cách chính xác. Trong chương trình toán học ở bậc tiểu học, ta sẽ có một số phương đơn giản và cụ thể để so sánh hỗn số.

Trong bài viết này hãy cùng thayphu khám phá chi tiết hơn về cách so sánh hỗn số và áp dụng chúng vào các bài tập cụ thể nhé.

Các cách để so sánh hỗn số

Cách 1: chuyển hỗn số về dạng phân số

Phương pháp: Cách đơn giản nhất để so sánh hai hỗn số đó là ta chuyển cả hai hỗn số cần so sánh về dạng phân số.

Ví dụ: So sánh hai hỗn số sau: 3 ¾ < 4 ¼.

Ta có:

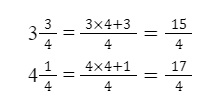
Vì 2 phân số có cùng mẫu số, mà 15 < 17 nên 15/4 < 17/4

Vậy 3 ¾ < 4 ¼.

Cách 2: So sánh phần nguyên trước rồi so sánh phần phân số

Phương pháp: Muốn so sánh hai hỗn số mà không cần chuyển hỗn số về dạng phân số, ta có thể so sánh trực tiếp hai hỗn số như sau:

• So sánh phần nguyên của cả hai hỗn số, hỗn số nào có giá trị phần nguyên lớn hơn thì lớn hơn và ngược lại.
• Nếu cả hai hỗn số đều có phần nguyên bằng nhau thì ta tiếp tục so sánh đến phần phân số, nếu phần phân số của hỗn số nào có giá trị lớn hơn thì lớn hơn và ngược lại.

Ví dụ 1: So sánh hai hỗn số sau: 4 ⅔ < 5 ½

Quan sát cả hai hỗn số, ta thấy:

Hỗn số 4 ⅔ có phần nguyên là 4

Hỗn số 5 ½ có phần nguyên là 5

Mà 4 < 5 vậy ta có thể suy ra 4 ⅔ < 5 ½.

Ví dụ 2: So sánh hai hỗn số sau: 5 ¾ và 5 ⅔

Quan sát cả hai hỗn số, ta thấy hai hỗn số có phần nguyên bằng nhau là 5.

Vậy ta sẽ so sánh phần phân số, ta có:

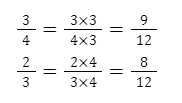
Vì 9/12 > 8/12 nên suy ra ¾ > ⅔

Vậy 5 ¾ > 5 ⅔.

Các quy tắc khi so sánh hỗn số

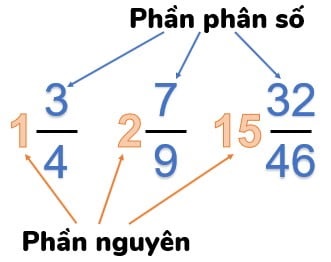
• So sánh khi cùng có phần nguyên: Nếu hai hỗn số có cùng phần nguyên, chúng ta chỉ cần so sánh phân số của chúng.
• So sánh khi có phần phân số khác nhau: Nếu hai hỗn số có phần nguyên bằng nhau, ta chỉ cần so sánh hai phần phân số bằng phương pháp so sánh bình thường.
• So sánh khi có phần nguyên khác nhau: Nếu hai hỗn số có phần nguyên khác nhau, chúng ta cần so sánh phần nguyên trước. Nếu phần nguyên khác nhau, hỗn số lớn hơn là hỗn số có phần nguyên giá trị lớn hơn. Nếu phần nguyên bằng nhau, chúng ta tiếp tục so sánh phân số.
• So sánh với số nguyên: Khi so sánh một hỗn số với một số nguyên, chúng ta có thể chuyển đổi hỗn số thành dạng phân số hoặc số thập phân. Khi đó, ta có thể dễ dàng so sánh với số nguyên.
• So sánh với số thập phân: Khi so sánh một hỗn số với một số thập phân, chúng ta cần chuyển đổi số thập phân thành một hỗn số bằng cách biểu diễn phần nguyên là phần nguyên của số thập phân và phân số là phần thập phân hoặc ngược lại.

Các bài tập luyện tập về hỗn số và so sánh hỗn số

Bài tập 1: Một con gà nặng 2 ⅚ kg, con vịt cân nặng 3 ⅞ kg. Vậy tổng số cân nặng của cả hai con gà và vịt là bao nhiêu ki-lô-gam?

1. 158/24

2. 2/3

3. 24/140

4. 161/24

Đáp án: D

Bài tập 2: Một cửa hàng có 75 ⅖ kg thóc. Buổi sáng cửa hàng bán được 12 ⅔ kg thóc. Buổi chiều cửa hàng bán được số thóc gấp 2 lần buổi sáng. Vậy sau cả hai buổi, cửa hàng còn lại ki-lô-gam thóc.

1. 30 ⅕ kg thóc
2. 38 kg thóc
3. 37 ⅖ kg thóc
4. 37 ¾ kg thóc
5. Đáp án: C

Bài tập 3: Hãy tính kết quả rồi so sánh giá trị của hai số A và B sau đây:

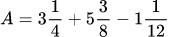và

1. A < B
2. A > B
3. A = B
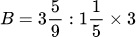
4. A ≥ B

Đáp án: A

Bài tập 4: Một người đạp xe được 4 ⅕ km trong một giờ đầu tiên. Giờ thứ hai người đó đi được 5 ⅘ km. Vậy người đó phải đạp xe với quãng đường dài bao nhiêu ki-lô-mét nữa để đi hết đoạn đường đó, biết rằng đoạn đường dài 16km.

1. 4 ⅗ km

2. 6 km

3. 6 ¾ km

4. 5 ⅖ km

Đáp án: B

Kết luận

So sánh hỗn số là một kỹ năng tuy cơ bản nhưng cũng rất quan trọng trong toán học và nó có ứng dụng rộng trong cuộc sống hàng ngày. Qua bài viết này, thayphu mong rằng các bạn đã nắm vững các phương pháp để so sánh hai hỗn số. Hiểu rõ các phương pháp so sánh này các bạn có thể nắm vững và so sánh các giá trị hỗn số một cách chính xác và tự tin hơn. Ngoài ra, nắm vững những kiến thức cơ bản này chính là nền tảng để ta có thể giải các dạng toán nâng cao hơn.