Bài tập xét dấu tam thức bậc 2 và cách giải chi tiết

Tổng hợp các dạng bài tập xét dấu tam thức bậc 2 thường gặp trong đề thi và hướng dẫn giải chi tiết, dễ hiểu nhất dành cho các em.

Bài tập xét dấu tam thức bậc 2 là dạng bài rất dễ bắt gặp trong các đề thi quan trọng. Để làm tốt các em cần nắm vững các định lý, công thức để vận dụng linh hoạt trong từng trường hợp. Sau đây là tổng hợp các nội dung cốt lõi về lý thuyết và các dạng bài tập ứng dụng, hãy cùng thayphu theo dõi nhé!

Tìm hiểu kiến thức về dấu của tam thức bậc hai

Lý thuyết về dấu của tam thức bậc 2

Tam thức bậc 2 là biểu thức có dạng ax^2 + bx + c = 0 với a, b, c là các hệ số cho trước và a khác 0.

Nghiệm của phương trình ax^2 + bx + c = 0 chính là nghiệm của tam thức bậc 2.

Ta có Δ = b^2 - 4ac là biệt thức và Δ’ = b’^2 - ac biệt thức thu gọn của tam thức bậc 2.

Định lý dấu của tam thức bậc 2

Cho f(x) = ax^2 + bx + c = 0 là tam thức bậc 2 có a khác 0 và Δ = b^2 - 4ac.

• Theo định lý thuận ta có:

+ Nếu Δ > 0 thì f(x) luôn cùng dấu với a (với mọi x thuộc R)

+ Nếu Δ = 0 thì f(x) có duy nhất 1 nghiệm là x = -b/2a.

Lúc này f(x) sẽ cùng dấu với a (mọi x khác -b/2a)

+ Nếu Δ < 0 thì f(x) sẽ có 2 nghiệm x1, x2 (x1 < x2).

Như vậy f(x) cùng dấu với a với mọi x thuộc (âm vô cực; x1) U (x2; dương vô cực). Tương tự f(x) trái dấu với a khi x1 < x < x2.

Lưu ý: Khi gặp bài tập xét dấu tam thức bậc 2 các em cần nhớ trong khoảng 2 nghiệm thì f(x) trái dấu với a. Và ngược lại ngoài khoảng 2 nghiệm thì f(x) cùng dấu với a.

• Theo định lý đảo dấu của tam thức bậc 2:

Nếu tồn tại số α thỏa điều kiện α.f(x) < 0 thì f(x) có 2 nghiệm phân biệt x1, x2 : x1 < α < x2.

Các bước xét dấu tam thức bậc 2

Để làm các bài tập xét dấu tam thức bậc 2, chúng ta thực hiện theo các bước như sau:

• Đầu tiên, tính Δ và tìm nghiệm của tam thức bậc 2 bằng cách bấm máy.
• Tiếp theo lập bảng xét dấu dựa theo hệ số a.
• Cuối cùng xét dấu và đưa ra kết luận.

Ứng dụng dấu tam thức bậc 2

Trong cả 2 trường hợp a > 0 và a < 0 thì:

• Nếu Δ > 0 thì f(x) có đủ cả 2 loại dấu dương & âm
• Nếu Δ <= thì f(x) chỉ có 1 loại dấu âm hoặc dương.

Từ đó ta có các bài toán với tam thức bậc 2: ax^2 + bx + c = 0, a khác 0 như sau:

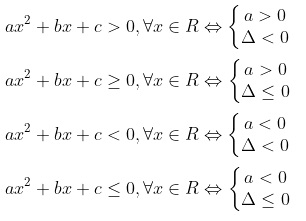
Các dạng bài tập xét dấu tam thức bậc 2

Sau khi nắm vững phần lý thuyết, các em cần thực hành áp dụng ngay vào các dạng bài tập để hiểu bài. Dưới đây là một số đề bài và hướng dẫn giải chi tiết cho các em tham khảo:

Thực hành ngay với các bài tập xét dấu tam thức bậc 2

Bài 1

Xét dấu tam thức bậc 2 f(x) = 3x^2 + 2x - 5

Hướng dẫn giải:

Theo đề ra ta có Δ = b^2 - 4ac = 27 > 0

Như vậy phương trình f(x) = 0 sẽ có 2 nghiệm phân biệt x1, x2 trong đó x1 = -5/3 và x2 = 1.

Tiến hành lập bảng xét dấu sau:

Kết luận f(x) < 0 khi x thuộc (-5/3;1)

f(x) > 0 khi x thuộc (âm vô cực; -5/3) U (1;dương vô cực).

Bài 2

Xét dấu biểu thức cho sau:

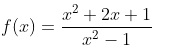
Hướng dẫn giải:

Tiến hành xét x^2 + 2x + 1 = 0 ⇔ x = -1 (a>0)

x^2 - 1 = 0 ⇔ x = -1 hoặc x = 1 (a>0).

Từ đó ta có bảng xét dấu:

Dựa vào bảng xét dấu ta kết luận:

f(x) > 0 khi x thuộc khoảng (âm vô cực; -1) U (1; dương vô cực)

f(x) < 0 khi x thuộc khoảng (-1; 1).

Bài 3

1. Giải bất phương trình -3x^2 + 7x - 4 = 0

Ta đặt f(x) = -3x^2 + 7x - 4

-3x^2 + 7x - 4 = 0 khi x = 1 hoặc x = 4/3

Lập bảng xét dấu:

Kết luận bất phương trình có tập nghiệm là S = (âm vô cực; 1) U (4/3; dương vô cực).

2. Giải bất phương trình

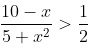
Khi gặp các bất phương trình hữu tỉ như vậy chúng ta cần biến đổi (rút gọn hoặc quy đồng) để có bất phương trình tích hoặc thương của các nhị thức bậc nhất và tam thức bậc 2. Sau đó mới lập bảng xét dấu và đưa ra kết luận.

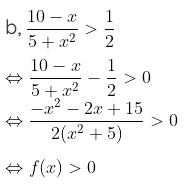
Lập bảng xét dấu cho vế trái của bất phương trình ta có:

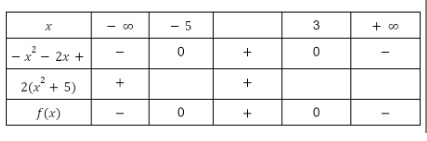
Kết luận tập nghiệm của bất phương trình là S = (-5;3).

Bài tập tự luyện

Bài 1 - Tìm m sao cho các bất phương trình đã cho sau vô nghiệm:

1. 5x^2 - x + m <= 0
2. (m-1)x^2 -(2m - 1)x > m - 3
3. x^2 - 2mx + m + 12 < 0
4. x^2 + 3mx - 9 < 0
5. x^2 + 3x - 9m <= 0

Bài 2 - Tìm m sao cho các bất phương trình sau chỉ có duy nhất một nghiệm:

1. -2x^2 - mx + m^2 - 1 >= 0
2. (m-1)x^2 - (2m - 1)x > -m-3
3. 2mx^2 + x - 3 >= 0

Trên đây là tổng hợp kiến thức và các dạng bài tập xét dấu tam thức bậc 2 cùng phương pháp giải đầy đủ và chi tiết nhất. Hy vọng các em có thể học tốt, dễ hiểu và áp dụng thành công vào các đề thi. Chương trình môn Toán sẽ còn rất nhiều nội dung thú vị khác, hãy cùng theo dõi kênh thường xuyên để cập nhật bài học hay nhé!