Ba đường conic: lý thuyết, công thức và ứng dụng

Giới thiệu về ba đường conic cơ bản: parabol, hypebol và elip. Chúng ta sẽ cùng tìm hiểu định nghĩa, phương trình chính tắc và ứng dụng của mỗi loại đường conic.

Đường conic là một khái niệm trong toán học mô tả các đường cong được tạo thành từ các điểm có cách đều nhất định đối với một điểm và một đường thẳng. Có ba loại đường conic cơ bản: parabol, hypebol và elip. Trong toán học, đường conic là một khái niệm quan trọng và có ứng dụng rộng trong nhiều lĩnh vực.

Trong bài viết này, thayphu sẽ cùng các bạn học sinh tìm hiểu về định nghĩa, phương trình và ứng dụng của mỗi loại đường conic này nhé.

Kiến thức chung các bạn học sinh cần nắm

Đường elip

• Định nghĩa

Cho hai điểm cố định F1, F2 và có độ dài không đổi 2a lớn hơn F1F2. Hình elip (E) là tập hợp M điểm trên mặt phẳng sao cho M.F1 + M.F2 = 2a.

Điểm F1 và F2 được gọi là tiêu điểm của hình elip.

Độ dài F1.F2 = 2c được gọi là tiêu cự của hình elip (a > c).

• Phương trình chính tắc của hình elip

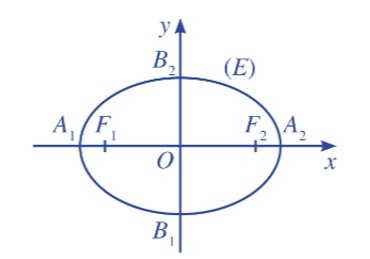
Để xác định phương trình chính tắc của một đường elip, người ta thường sử dụng hệ tọa độ Oxy, trong đó gốc O là trung điểm của hai tiêu điểm F1 và F2, trục Oy là đường trung trực của đoạn thẳng F1.F2.

Khi đó, phương trình chính tắc của hình elip có thể được viết là:

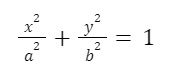
trong đó a > b > 0.

=> Đây được gọi là phương trình chính quy của hình elip.

Nếu điểm M( x, y) thuộc hình elip thì -a ≤ x ≤ a.

Đường hypebol

• Định nghĩa

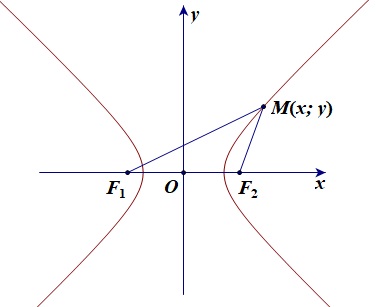
Cho hai điểm cố định F1, F2 và có độ dài không đổi là 2a nhỏ hơn F1.F2. Hypebol (H) là tập hợp M điểm trên mặt phẳng sao cho |M.F1 – M.F2| = 2a.

Điểm F1 và F2 được gọi là tiêu điểm của hypebol.

Độ dài F1.F2 = 2c được gọi là tiêu cự của hypebol (c > a).

• Phương trình chính tắc của hypebol

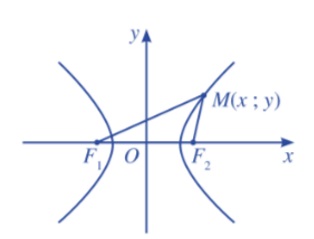
Để xác định phương trình chính tắc của đường hypebol, người ta thường sử dụng hệ tọa độ Oxy, gốc O là trung điểm của hai tiêu điểm F1 và F2, trục Ox là đường thẳng nối F1 và F2, trục Oy là đường trung trực của đoạn F1.F2 = 2c (c > 0 ).

Khi đó, phương trình chính quy của Hypebol có thể được viết là:

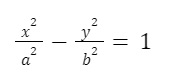
trong đó a > 0, b > 0.

=> Đây là phương trình chính tắc của Hypebol.

Nếu điểm M(x, y) thuộc hypebol thì x ≤ -a hoặc x ≥ a.

Đường parabol

• Định nghĩa

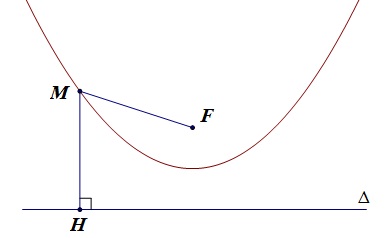
Cho điểm F và đường thẳng Δ không đi qua F. Parabol (P) là tập hợp các điểm M cách đều F và Δ.

F được gọi là tiêu điểm và Δ được gọi là đường tham chiếu của parabol (P).

điểm quy chuẩn

• Phương trình chính tắc của parabol

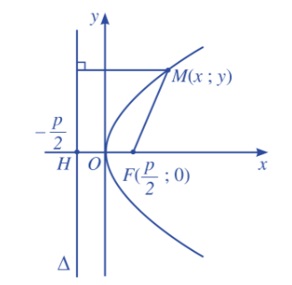
Để xác định phương trình chính tắc của parabol, người ta thường sử dụng hệ tọa độ Oxy. Gốc tọa độ O nằm tại trung điểm đoạn thẳng nối F và điểm tiếp xúc vuông góc với Δ (ký hiệu là H). Điểm F nằm trên trục Ox.

Khi sử dụng hệ tọa độ trên, phương trình chính tắc của parabol có thể được viết là

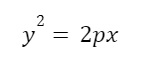
trong đó p là số thực dương (p > 0).

Đối với một parabol (P), có phương trình chuẩn y^2 = 2px (p > 0):

• Điểm F được gọi là tiêu điểm của parabol.
• Đường thẳng Δ được gọi là đường chuẩn của parabol.
• Nếu điểm M(x, y) thuộc một parabol (P) thì x phải lớn hơn hoặc bằng 0.

Bảng công thức

Ba đường conic: Elip, Hypebol, Parabol gồm phương trình chính tắc, tọa độ các đỉnh, tọa độ tiêu điểm, tiêu cự, tâm sai, độ dài trục lớn, trục bé, trục thực, trục ảo, phương trình đường chuẩn, tiệm cận, phương trình tiếp tuyến,.... Có rất nhiều thông tin cần nắm về 3 đường conic. Vì vậy, dưới đây là bảng tóm gọn có các kiến thức cần nhớ về ba đường conic cho các bạn học sinh dễ dàng nắm rõ:

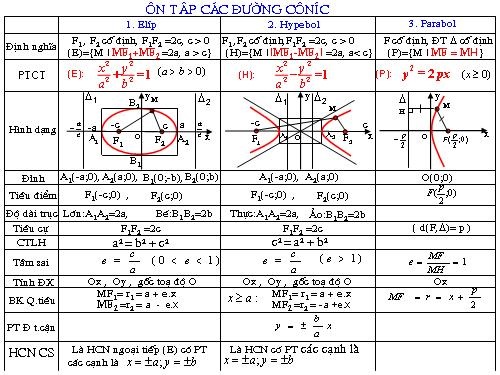
Ứng dụng

• Parabol có nhiều ứng dụng trong cơ học, vật lý và kỹ thuật, bao gồm đèn pha ô tô, thiết kế động cơ rocket, và thiết kế các cầu nâng.
• Hypebol có ứng dụng trong kỹ thuật điện, quang học và thiết kế antenna.
• Elip có ứng dụng trong thiết kế đèn, thiết kế ống kính, và tạo hình trong đồ họa máy tính.
• Mô hình nguyên tử: Năm 1911, nhà vật lý người Anh Ernest Rutherford đề xuất mô hình nguyên tử hành tinh, trong đó một hạt nhân nhỏ nằm ở trung tâm của nguyên tử và các electron quay quanh hạt nhân theo quỹ đạo hình elip, giống như các hành tinh quay quanh mặt trời.
• Giao thoa sóng: Trong vật lý, khi hai sóng gặp nhau, chúng giao thoa và tạo thành một hyperbol. Các vân giao thoa trong hiện tượng này có hình dạng như hyperbol.
• Gương parabol và hệ thống lấy nét: Gương parabol được sử dụng trong nhiều ứng dụng trong đó tia sáng chiếu vào gương parabol sẽ hội tụ tại tiêu điểm và phản xạ các tia song song với trục của parabol.
• Đèn pha: Gương parabol được sử dụng phổ biến trong thiết kế đèn pha ô tô. Bề mặt của đèn pha là một vòng tròn quay quanh trục của nó, với bóng đèn đặt ở tiêu điểm của parabol. Khi ánh sáng từ bóng đèn chiếu vào bề mặt đèn pha sẽ được tập trung và phản xạ thành các tia sáng song song, giúp người lái xe nhìn rõ trong điều kiện ánh sáng yếu hoặc vào ban đêm.
• Gương thu và truyền vệ tinh: Ăng ten trên vệ tinh thường được thiết kế dưới dạng gương parabol. Các điểm thu và phát tín hiệu của vệ tinh được đặt tại tiêu điểm của parabol, giúp tập trung tín hiệu vào và ra ăng ten, nâng cao chất lượng truyền tín hiệu từ vệ tinh tới trái đất.