Cách xét dấu hàm số bậc 3 chi tiết và bài tập vận dụng

Phương pháp xét dấu hàm số bậc 3, mẹo xét dấu nhanh bằng đồ thị hàm số chỉ trong 10 giây và bài tập vận dụng của chúng.

Hàm bậc 3 là một dạng hàm đa thức có bậc cao nhất là 3. Khi xét dấu của hàm bậc 3, chúng ta quan tâm đến việc tìm hiểu các điểm cực trị và điểm uốn của hàm để xác định sự tăng giảm và hình dạng của đồ thị hàm số.

Vì vậy, bài viết này thayphu sẽ hướng dẫn cho các bạn học sinh phương pháp xét dấu hàm số bậc 3, mẹo xét dấu nhanh để áp dụng vào các dạng toán khác nhau nhé.

Phương pháp xét dấu hàm số bậc 3

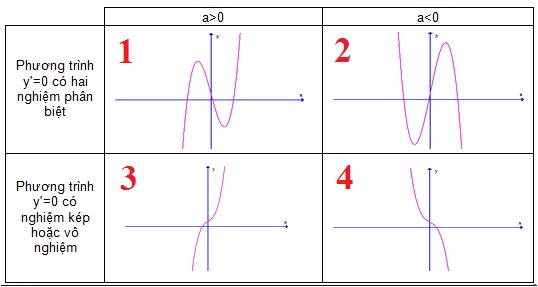
Dưới đây là các bước cơ bản để xét dấu hàm số bậc 3:

• Bước 1: Tìm miền xác định của hàm số

Để xác định miền xác định của hàm bậc 3, ta dùng phương pháp giải phương trình tìm tử số và mẫu số của hàm số. Bước này giúp ta xác định được các giới hạn về giá trị của biến độc lập trong miền xác định.

• Bước 2: Tìm các điểm cực trị

Để tìm các điểm cực trị của hàm bậc 3, chúng ta cần tìm các giá trị của biến độc lập mà hàm có thể đạt cực đại hoặc cực tiểu. Chúng ta thực hiện bằng cách giải phương trình f'(x) = 0, trong đó f'(x) là đạo hàm của hàm bậc 3 đã cho.

• Bước 3: Tìm các điểm uốn

Điểm uốn là các điểm trên đồ thị của hàm bậc 3 mà tại điểm này hình dạng của đồ thị thay đổi từ lên thành xuống hoặc ngược lại. Để tìm các điểm uốn, chúng ta cần giải phương trình f''(x) = 0, trong đó f''(x) là đạo hàm hai lần của hàm bậc 3. Hay nói cách khác, f’’(x) là đạo hàm của hàm số f’(x).

• Bước 4: Xét dấu và vẽ đồ thị

Dựa vào các điểm cực trị và điểm uốn ta đã tìm được trước đó, chúng ta có thể xác định sự tăng giảm và hình dạng của đồ thị hàm bậc 3. Bằng cách xét dấu của hàm và các khoảng giá trị của biến độc lập, từ đó ta có thể vẽ đồ thị chi tiết của hàm.

Bài tập ví dụ: Hãy xét dấu của hàm số: f(x) = x^3 - 6x^2 + 9x

• Bước 1: Miền xác định của hàm là tất cả các giá trị thực (với mọi x thuộc R).
• Bước 2: Tìm các điểm cực trị bằng cách giải phương trình f’(x) = 0.

f’(x) = 3x^2 - 12x + 9

Giải phương trình f’(x) = 0, ta có:

3x^2 - 12x + 9 = 0

⇔ x^2 - 4x + 3 = 0

⇔ (x - 1)(x - 3) = 0

Vậy, các điểm cực trị của hàm là x = 1 và x = 3.

• Bước 3: Tìm các điểm uốn bằng cách giải phương trình f’’(x) = 0.

f''(x) = 6x - 12

Giải phương trình f''(x) = 0, ta có:

6x - 12 = 0

Suy ra, x = 2 là điểm uốn của hàm.

• Bước 4: Xét dấu và vẽ đồ thị.

Dựa vào các điểm cực trị và điểm uốn, ta có thể xác định sự tăng giảm và hình dạng của đồ thị hàm bậc 3.

Xét x < 1, f’(x) < 0, nghĩa là hàm giảm trên khoảng (-∞, 1).

Xét 1 < x < 2, f’(x) > 0, nghĩa là hàm tăng trên khoảng (1, 2).

Xét 2 < x < 3, f’(x) < 0, nghĩa là hàm giảm trên khoảng (2, 3).

Xét x > 3, f’(x) > 0, nghĩa là hàm tăng trên khoảng (3, +∞).

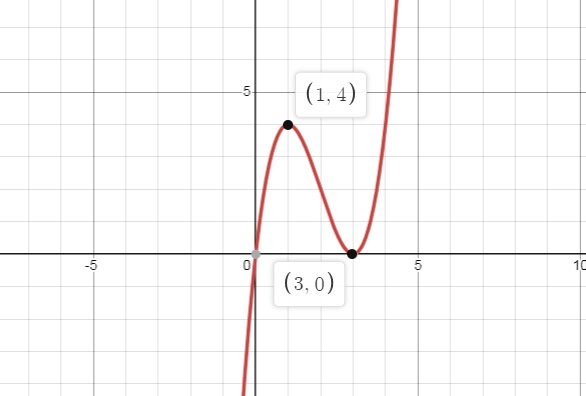
Vậy hàm số: f(x) = x^3 - 6x^2 + 9x có hình dạng như đồ thị trên.

Mẹo xét dấu đồ thị hàm số bậc 3 cực nhanh

Cho hàm số bậc ba như sau: y = ax^3 + bx^2 + cx + d

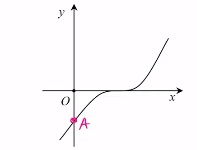
1. Xét dấu của a

Từ hình vẽ chúng ta có thể tìm được giới hạn L= lim x→+∞y, từ đó suy ra:

• L=+∞ ⇔ a > 0.
• L=−∞ ⇔ a < 0.

Hay nói cách khác, ta có thể nhìn dáng của đồ thị để xác định:

• Hàm số bậc 3 có đồ thị đi lên thì a > 0
• Hàm số bậc 3 có đồ thị đi xuống thì a < 0

2. Xét dấu của d

Ta có điểm A(0;d) là giao điểm của đồ thị hàm số với trục tung (đồ thị giao với Oy tại điểm A). Ta có:

• A nằm phía trên trục hoành ⇔ d > 0.
• A nằm phía dưới trục hoành ⇔ d < 0.
• A nằm trên trục hoành ⇔ d = 0.

3. Xét dấu của b và c

Cũng tại điểm A(0;d) trên đồ thị đã cho. Để xét dấu của c, ta quan sát:

• Tại điểm A nếu đồ thị đi lên ⇔ c > 0
• Tại điểm A nếu đồ thị đi xuống ⇔ c < 0

Để xét dấu điểm b, ta quan sát điểm uốn của hàm số của đồ thị trên:

• Nếu hoành độ của điểm uốn x > 0 thì a, b trái dấu
• Nếu hoành độ của điểm uốn x < 0 thì a, b cùng dấu

Ngoài ra, ta có bảng xét dấu nhanh các dạng đồ thị như sau:

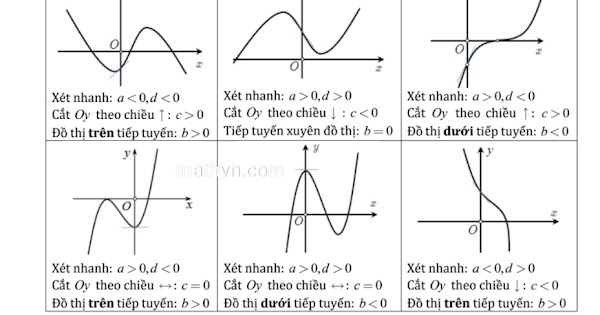
=> Từ các điểm trên, ta có thể dễ dàng xét dấu hàm số bậc 3 cực nhanh. Tuy nhiên, mẹo này cũng có nhược điểm là ở các dạng toán không cho sẵn đồ thị hàm số hoặc không có thông tin để vẽ được đồ thị thì rất khó để xác định được dấu của hàm số. Lúc này, các bạn học sinh vẫn có thể áp dụng phương pháp xét dấu cơ bản để giải các dạng toán đó.

Bài tập vận dụng

Cho hàm số y = ax^3 + bx^2 + cx + d có đồ thị như hình vẽ bên:

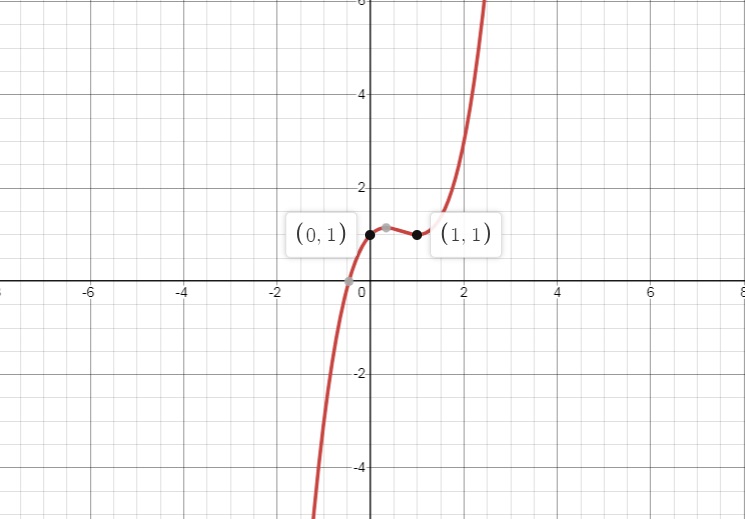
Mệnh đề nào sau đây là đúng trong các mệnh đề dưới đây:

1. ad < 0, bc < 0
2. ad > 0, bc > 0
3. ad < 0, bc > 0
4. ad > 0, bc < 0

Gợi ý lời giải:

Từ hình vẽ đã cho, đồ thị đi lên ⇔ a > 0

Cho điểm A là điểm giao của đồ thị với trục Oy ⇔ d > 0

Cũng tại điểm A (0;1), đồ thị đi lên ⇔ c > 0

Từ đồ thị đã cho, ta thấy hoành độ của điểm uốn x > 0 ⇔ a, b trái dấu, mà a > 0 => b < 0

=> ad > 0, bc < 0. Vậy ta chọn D.

Qua bài viết trên, thayphu.net đã giới thiệu đến các bạn học sinh phương pháp xét dấu hàm số bậc 3 và mẹo để xét dấu nhanh bằng đồ thị hàm số. Mỗi phương pháp đều có ưu nhược điểm riêng nên vì vậy các em hãy nắm vững cả 2 phương pháp và tính chất cơ bản của chúng bằng cách luyện tập thật tốt để có thể vận dụng vào nhiều dạng toán nâng cao khác nhau nhé.