Phương pháp xác định vị trí tương đối của hai đường thẳng chi tiết
Cách xét vị trí tương đối của hai đường thẳng chi tiết và hay nhất. Đi kèm các bài tập ứng dụng dễ hiểu giúp các em học tốt!
Vị trí tương đối của hai đường thẳng trong chương trình Toán lớp 10 là một phần kiến thức cơ bản đối với cấp THPT. Bài viết này sẽ tổng hợp chi tiết cả về lý thuyết, các phương pháp quan trọng và các dạng bài tập chọn lọc. Các em cùng theo dõi để nắm vững kiến thức và dễ dàng chinh phục các đề bài nhé!
 Tìm hiểu về vị trí tương đối hai đường thẳng
Tìm hiểu về vị trí tương đối hai đường thẳng
Trường hợp khi xét vị trí tương đối của hai đường thẳng
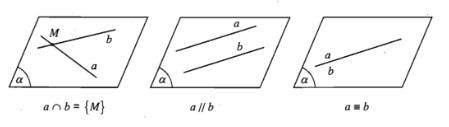
Xét vị trí tương đối của hai đường thẳng trong không gian có thể xảy ra 2 trường hợp như sau:
-
Hai đường thẳng đồng phẳng
Trường hợp này hay còn gọi là hai đường thẳng cùng ở trên một mặt phẳng. Và sẽ có các vị trí tương đối như là:
- Cắt nhau khi 2 đường thẳng chỉ có duy nhất một điểm chung
- Song song khi 2 đường thẳng không có bất kỳ điểm chung nào
- Trùng nhau khi 2 đường thẳng này có nhiều hơn 2 điểm chung
-
Hai đường thẳng không đồng phẳng
Đối với trường hợp này thì 2 đường thẳng sẽ không có điểm chung hay còn gọi là 2 đường thẳng chéo nhau.
Phương pháp xác định vị trí tương đối của hai đường thẳng
Để xét vị trí tương đối của 2 đường thẳng chúng ta có thể dựa trên 2 tiêu chí đó là số điểm chung và sự đồng phẳng. Tuy nhiên việc áp dụng 2 tiêu chí này trong Oxyz sẽ không đem lại hiệu quả. Như vậy để việc xác định nhanh và chính xác ta sử dụng tính chất có hướng và xét theo sơ đồ.
Tham khảo các dạng bài thường gặp và phương pháp giải chi tiết
Dạng 1
Chúng ta sẽ chỉ ra vị trí tương đối của hai đường thẳng cho trước. Sau đó tiến hành tìm tham số m để các đường thẳng thỏa mãn vị trí tương đối cho trước.
Ta cho 2 đường thẳng d: y = ax + b (với a khác 0) và d’: y = a’x + b’ (với a’ khác 0). Lúc này xét các trường hợp:
- d song song với d’ ⇔ a = a’ và b khác b’
- d cắt d’ ⇔ a khác a’
- Cuối cùng là d trùng với d’ ⇔ a = a’ và b = b’
Bài tập ứng dụng
Cho các cặp đường thẳng bên dưới và yêu cầu xét vị trí tương đối:
-
y = 2x + 3 và y = -3x - 5
Ta có đồ thị hàm số y = 2x + 3 sẽ có hệ số góc là k1 = 2
Tương tự đồ thị hàm số y = -3x - 5 sẽ có hệ số góc là k2 = -3
Xét thấy k1 khác k2 nên kết luận được 2 đồ thị hàm số trên cắt nhau.
-
y = 5x - 3 và y = 5x + 7
Ta có đồ thị hàm số y = 5x - 3 sẽ có hệ số góc là k1 = 5
Tương tự đồ thị thị hàm số thứ 2 y = 5x + 7 cũng có hệ số góc là k2 = 5
Xét thấy k1 = k2 nên ta kết luận đồ thị của 2 hàm số trên song song với nhau.
-
y = -2x - 1 và y = ½ x + 1
Ta có đồ thị hàm số y = -2x - 1 sẽ có hệ số góc k1 = -2
Tương tự đồ thị hàm số y = ½ x + 1 sẽ có hệ số góc là k2 = ½
Xét thấy k1 khác k2 nên kết luận đồ thị của 2 hàm số trên cắt nhau.
Bên cạnh đó k1.k2 = -2. ½ = -1 nên hai đường thẳng này vuông góc với nhau.
Dạng 2 - Viết phương trình đường thẳng
Với dạng này chúng ta thực hiện theo thứ tự các bước:
- Xác định hệ số bằng cách sử dụng vị trí tương đối của hai đường thẳng đi kèm với các kiến thức.
- Xét y = ax + b (với điều kiện a khác 0, b khác 0) là phương trình đường thẳng cắt trục tung tại điểm A (0 ; b) và cắt trục trục hoành tại điểm B (-b/a ; 0).
- Điểm M có tọa độ (x0; y0) thuộc đường thẳng y = ax + b khi và chỉ khi y0 = ax0 + b.
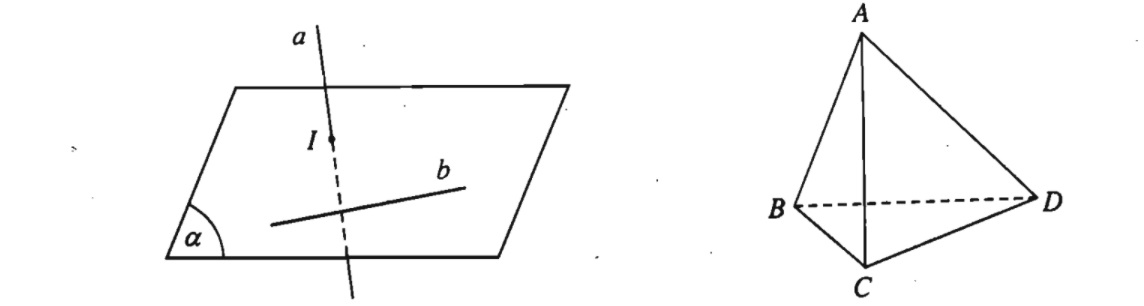
Dạng bài yêu cầu viết phương trình đường thẳng
Bài tập ứng dụng
-
Cho đường thẳng y = 3x + 2, yêu cầu tìm đường thẳng song song và cắt trục tung tại điểm có tung độ bằng 5.
Gọi đường thẳng cần tìm là (d) và có dạng y = ax + b
Theo đề ra thì (d) song song với đường thẳng y = 3x + 2 nên suy ra a = 3.
(d) còn cắt trục tung tại điểm có tung độ = 5 suy ra x = 0 và y = 5 ⇔ b = 5.
Với a = 3 và b = 5 ta kết luận đường thẳng cần tìm chính là y = 3x + 5.
-
Cho đường thẳng y = (½)x + 1 và đi qua điểm A(2;1), yêu cầu tìm đường thẳng vuông góc với nó.
Ta gọi đường thẳng cần tìm là (d’) có dạng: y = ax + b
Theo đề ra (d’) vuông góc với đường thẳng y = (½)x + 1 suy ra a.½ = -1 => a = -2.
Lúc này (d’) sẽ có dạng là y = -2x + b.
Tiếp đó vì (d’) đi qua điểm A (2;1) nên ta được 1 = -2.2 + b => b = 5.
Với a = -2 và b = 5 ta kết luận đường thẳng cần tìm là y = -2x + 5.
Dạng 3
Tìm điểm cố định để phương trình đường thẳng d luôn đi qua với mọi tham số m
Khi gặp dạng bài này chúng ta áp dụng phương pháp như sau:
- Gọi điểm M tọa độ (x;y) là điểm cần tìm, khi đó điểm M(x;y) thỏa mãn phương trình đường thẳng d.
- Chuyển phương trình đường thẳng d về thành phương trình bậc nhất ẩn m.
- Ta có phương trình bậc nhất ax + b = 0 luôn đúng với điều kiện a = b = 0.
- Giải điều kiện ta được x, y cần tìm.
- Kết luận điểm cố định là M(x;y).
Bài tập ứng dụng
Hãy chứng minh rằng đường thẳng (d) có phương trình là y = (m + 1)x + 2x - m luôn đi qua một điểm cố định với mọi m.
Giải:
Ta gọi điểm M có tọa độ (x0; y0) là điểm cố định mà đường thẳng (d) luôn đi qua. Lúc này ta sẽ có:
y0 = (m + 1)x0 + 2x0 - m, với mọi m
y0 = mx + x0 + 2x0 - m, với mọi m
y0 = mx0 - 3x0 - m = 0, với mọi m
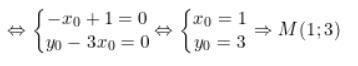
Kết luận với mọi m, đường thẳng (d) có phương trình y = (m + 1)x + 2x - m luôn đi qua 1 điểm cố định là M(1;3).
Trên đây là tổng hợp các lý thuyết, phương pháp và bài tập về cách xét vị trí tương đối của hai đường thẳng. Hy vọng bài viết hữu ích giúp các em chinh phục tốt các dạng bài này!


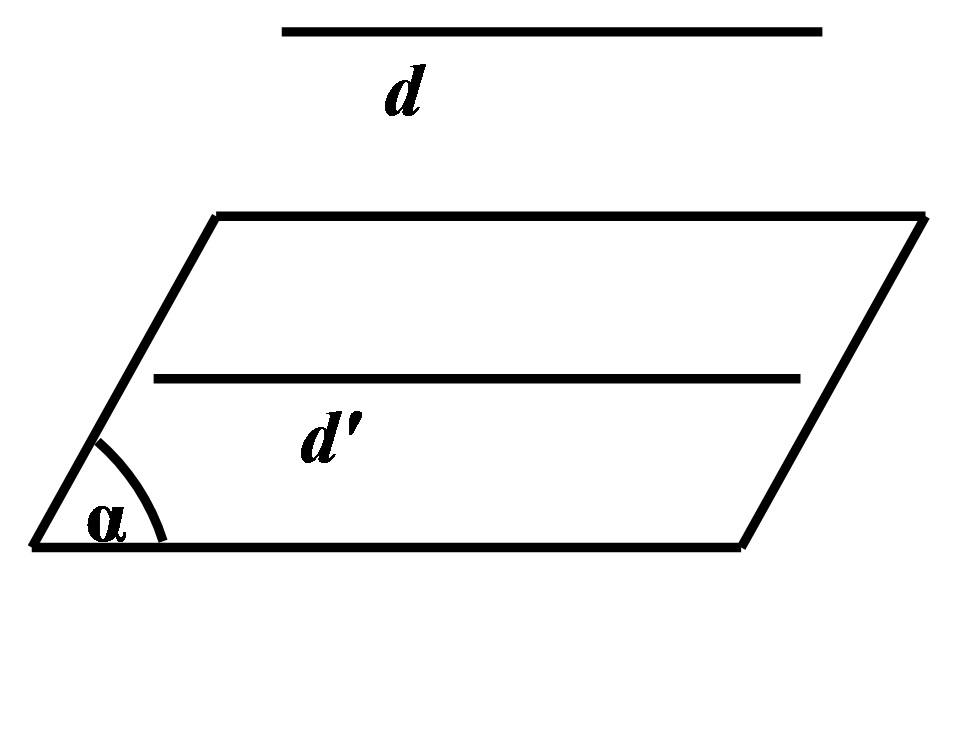
 Định nghĩa góc giữa hai đường thẳng
Định nghĩa góc giữa hai đường thẳng  Góc giữa hai vectơ
Góc giữa hai vectơ 