Cách tìm vectơ pháp tuyến của mặt phẳng chuẩn nhất

Cách tìm vectơ pháp tuyến trong không gian đơn giản nhất, cách tìm vectơ pháp tuyến của mặt phẳng và tính góc giữa hai mặt phẳng.

Ở bộ môn toán hình học lớp 12, chúng ta sẽ được tiếp xúc với vectơ pháp tuyến của mặt phẳng. Thông thường những câu hỏi về kiến thức này sẽ thường xuất hiện ở các bài kiểm tra. Chính vì vậy mà bạn cần nắm thật chắc cách tìm vectơ pháp tuyến. Hãy cùng thayphu theo dõi bài viết dưới đây nhé.

Vectơ pháp tuyến của mặt phẳng là gì?

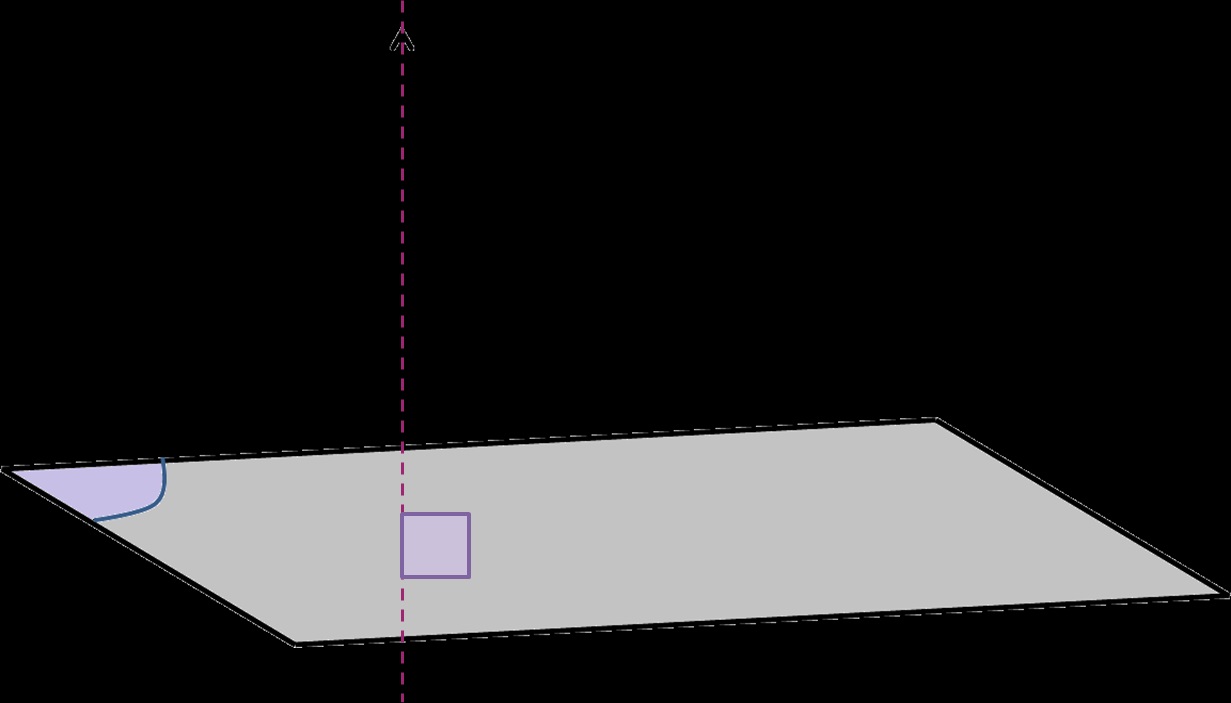
Khái niệm Vecto pháp tuyến của mặt phẳng

Cho một mặt phẳng (P) trong không gian. Có một vecto khác vecto không có phương vuông góc với mặt phẳng (P) đã cho trước thì lúc này nó được gọi là vectơ pháp tuyến của mặt phẳng đó.

Một số lưu ý về vecto pháp tuyến:

• Một mặt phẳng bất kỳ sẽ có vô số vectơ pháp tuyến và các vectơ này sẽ có cùng phương với nhau.
• Ngược lại, một vecto khác vecto khác không sẽ là vectơ pháp tuyến của vô số mặt phẳng trong không gian.
• Khi biết được một vectơ pháp tuyến và một điểm trong không gian thì một mặt phẳng sẽ được xác định.

Vector pháp tuyến của một mặt phẳng là một vectơ vuông góc với mặt phẳng đó, và được định nghĩa bởi tích vectơ của hai vectơ cùng thuộc mặt phẳng đó. Nó là một trong những khái niệm quan trọng trong hình học không gian và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau như vật lý, toán học, và kỹ thuật.

Cách tính vecto pháp tuyến của một mặt phẳng như sau:

• Đầu tiên, xác định phương trình của mặt phẳng.
• Sau đó, xác định hai vectơ bất kì cùng nằm trong mặt phẳng.
• Tính tích vectơ của hai vectơ đó.
• Vector thu được chính là vectơ pháp tuyến của mặt phẳng.

Khi đã biết vectơ pháp tuyến của một mặt phẳng, ta có thể sử dụng nó để tính các đại lượng khác liên quan đến mặt phẳng đó, chẳng hạn như khoảng cách từ một điểm đến mặt phẳng hay góc giữa hai mặt phẳng.

Vecto chỉ phương của một mặt phẳng

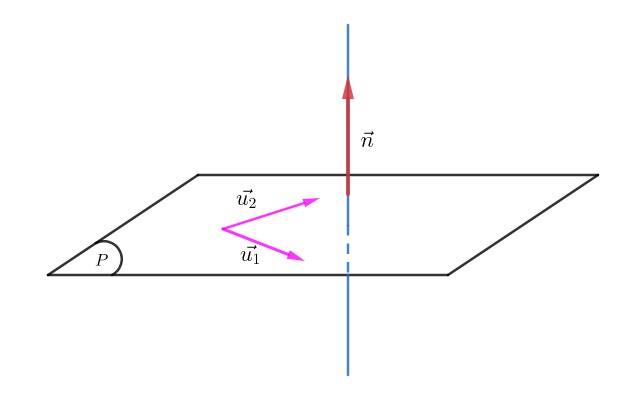
Vecto chỉ phương của một mặt phẳng

Một mặt phẳng trong không gian có thể được mô tả bằng một vectơ pháp tuyến và một vectơ chỉ phương. Vector chỉ phương của một mặt phẳng là một vectơ vuông góc với vectơ pháp tuyến của mặt phẳng đó và chỉ hướng của mặt phẳng.

Một số lưu ý về vecto chỉ phương của một mặt phẳng mà bạn cần biết:

• Ta có thể dễ dàng nhận thấy rằng vectơ chỉ phương và vecto pháp tuyến trong mặt phẳng hay không gian sẽ vuông góc với nhau.
• Nếu như ta lấy tích có hướng của hai vecto chỉ phương thì sẽ được một vectơ pháp tuyến của mặt phẳng đó. Trong hình học không gian Oxyz thì dạng toán này rất phổ biến. Bởi vậy nên bạn cần nắm chắc tính chất này để giải các bài tập.

Các vị trí tương đối của hai mặt phẳng

Trong không gian ba chiều, hai mặt phẳng có thể có vị trí tương đối như sau:

• Mặt phẳng cắt qua mặt phẳng khác: hai mặt phẳng cắt nhau tại một đường thẳng gọi là đường cắt. Điều này có thể xảy ra khi hai mặt phẳng không song song và không trùng nhau.
• Hai mặt phẳng song song và cách nhau một khoảng cách d: hai mặt phẳng không cắt nhau và không trùng nhau, nhưng nằm song song với nhau. Khoảng cách giữa hai mặt phẳng là độ dài đường vuông góc từ một điểm trên một mặt phẳng đến mặt phẳng còn lại.
• Hai mặt phẳng trùng nhau: hai mặt phẳng trùng nhau khi chúng có phương trình giống nhau.
• Hai mặt phẳng vuông góc với nhau: hai mặt phẳng vuông góc với nhau khi vectơ pháp tuyến của một mặt phẳng vuông góc với vectơ pháp tuyến của mặt phẳng còn lại.
• Hai mặt phẳng giao nhau một góc: hai mặt phẳng không cắt nhau nhưng không vuông góc với nhau. Góc giữa hai mặt phẳng được tính bằng góc giữa hai vectơ pháp tuyến của chúng.

Cụ thể khi xác định được vectơ pháp tuyến, ta sẽ có các trường hợp như sau:

Các công thức liên quan đến vecto pháp tuyến của mặt phẳng Oxyz

Công thức tìm vectơ pháp tuyến của mặt phẳng Oxyz

Có thể tìm vectơ pháp tuyến của một mặt phẳng bằng nhiều cách khác nhau, những phương pháp phổ biến nhất là sử dụng phương trình của mặt phẳng.

Với phương trình của mặt phẳng dạng tổng quát như sau:

ax + by + cz + d = 0

Trong đó: a, b, c là các hệ số không đồng nhất với nhau, thì vectơ pháp tuyến của mặt phẳng là vector (a, b, c).

Công thức tính khoảng cách từ một điểm đến một mặt phẳng

Trong không gian Oxyz, ta có mặt phẳng (P) có phương trình là Ax + By + Cz + D = 0 và một điểm M0(x0,y0,z0). Lúc này, khoảng cách từ điểm M 0 đến mặt phẳng (P) sẽ được tính theo công thức:

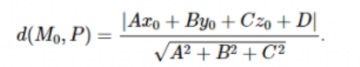
Công thức tính góc giữa hai mặt phẳng dựa vào vectơ pháp tuyến

Trong mặt phẳng Oxyz cho hai mặt phẳng (P1) và (P2) có phương trình cụ thể như sau:

(P1): A1x + B1y + C1z + D1 = 0

(P2): A2x + B2y + C2z + D2 = 0.

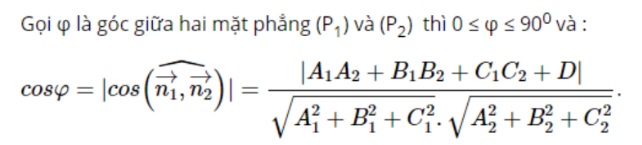
Bài tập áp dụng

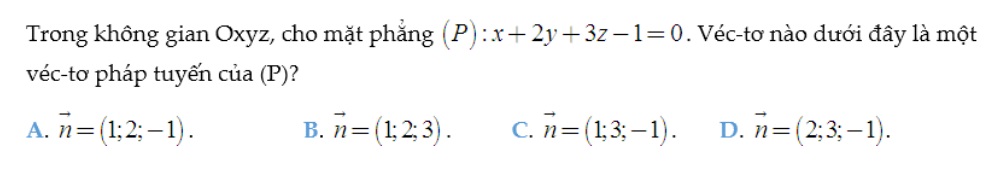
Câu hỏi xác định vectơ pháp tuyến trong kỳ thi THPTQG

Một số câu hỏi trắc nghiệm khác

Trên đây là toàn bộ kiến thức về vecto pháp tuyến của mặt phẳng mà chúng tôi muốn chia sẻ đến các bạn đọc. Mong rằng với những gì chia sẻ sẽ giúp các bạn hiểu rõ hơn về vecto pháp tuyến cũng như các công thức liên quan đến kiến thức hình học này.