Ứng dụng tích phân tính diện tích và thể tích trong hình học

Ứng dụng tích phân giúp tính diện tích và thể tích các hình khối phức tạp. Sử dụng rộng rãi quá trình tính toán, tiết kiệm thời gian và đảm bảo độ chính xác.

Tích phân là một chủ đề không còn xa lạ với những ai đã học toán cấp 3. Tuy nhiên, việc tính toán các bài toán liên quan đến diện tích và thể tích của các hình khối phức tạp có thể trở nên rất phức tạp và tốn nhiều thời gian.

Vậy ứng dụng tích phân trong hình học là gì? Hãy cùng Thayphu tìm hiểu thêm về ứng dụng này trong bài viết sau đây.

Ứng dụng tích phân tính diện tích hình phẳng

Trong ứng dụng tích phân diện tích hình phẳng sẽ được áp dụng theo 2 công thức cơ bản sau đây:

Hình phẳng giới hạn bởi một đường cong và trục hoành

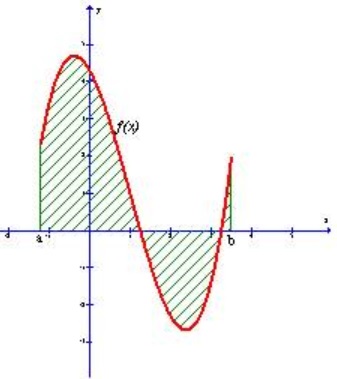
Trong ứng dụng tích phân diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y=f(x) liên tục ( như hình vẽ trên), trục hoành và hai đường x= a, x=b được tính theo công thức:

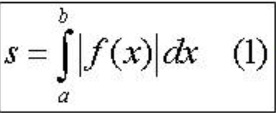
Mặt phẳng giới hạn bởi hai đường cong

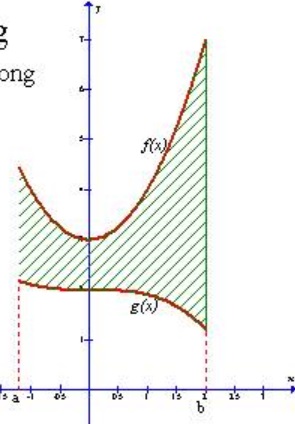
Diện tích S của hình phẳng giới hạn bởi đồ thị của hàm số y=f(x), y=g(x) liên tục và hai được thẳng x=a , x=b được tính theo công thức:

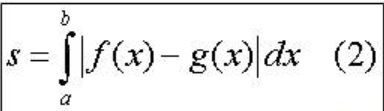
Ví dụ 1 : Tính diện tích hình phẳng giới hạn bởi: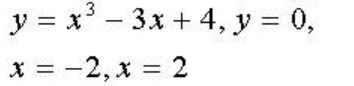

Lời giải

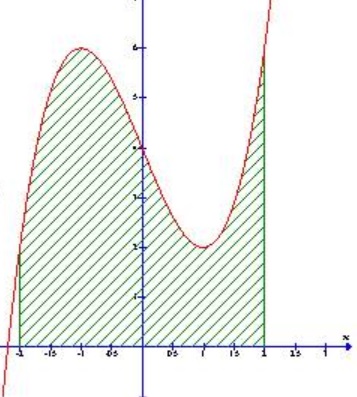
Diện tích cần tìm là :

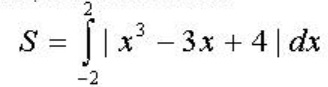
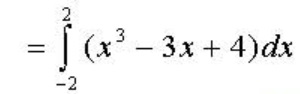
Nhấn máy tính để tính phương trình trên

=> Diện tích cần tìm là 16

Chú ý : Một số trường hợp thường là hình phẳng giới hạn bởi nhiều hơn 2 đồ thị và việc dựng các đồ thị này là tương đối dễ dàng. Ta nên kết hợp với việc vẽ đồ thị để phân chia thành các hình phẳng đơn giản.

Ví dụ 2: Tính diện tích hình phẳng H giới hạn bởi các đường : y= √x, y=6 - x , y= 0

Lời giải

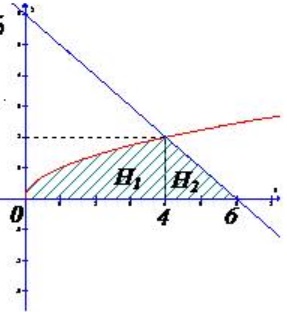
Ta có:

√x = 6 - x ⇔ x=4

√x = 0 ⇔ x=0 ; 6 - x = 0 ⇔ x = 6

Xét 2 trường hợp

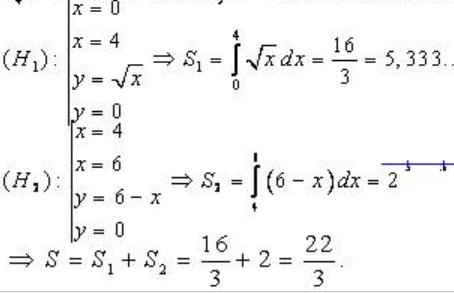
Ứng dụng tích phân tính thể tích

Ở ứng dụng tích phân ta sẽ tính được các thể tích của các khối khác nhau. Đây là một công thức khá đơn giản và dễ áp dụng trong mọi trường hợp:

Tính thể tích của tích phân

Tính thể tích vật thể

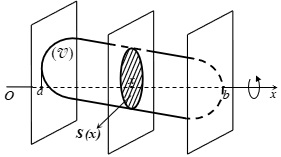
Trong ứng dụng tích phân chúng ta có một vật thể (H) được cắt bởi hai mặt phẳng (P) và (Q), vuông góc với trục Ox tại x = a và x = b (a < b). Một mặt phẳng tùy ý, vuông góc với Ox tại điểm x (a ≤ x ≤ b), sẽ cắt vật thể này thành một thiết diện có diện tích là S(x). Giả sử diện tích S(x) của thiết diện này là liên tục trên đoạn [a; b].

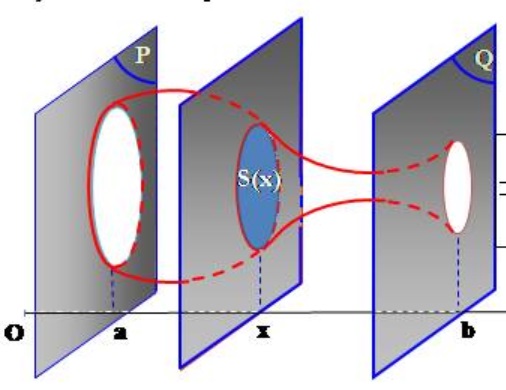
Ta có công thức

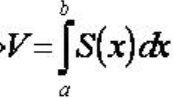
Ví dụ 1: Tính thể tích của vật thể nằm giữa 2 mặt phẳng x=-1 và x=1 . Biết rằng thiết diện của vật thể này bị cắt bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (-1<= x<= 1) là một hình vuông có cạnh 2√1 - x^2.

Lời giải

Diện tích thiết diện :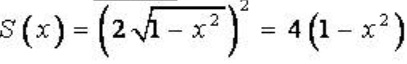

Từ đó ta áp dụng công thức: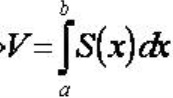

=>

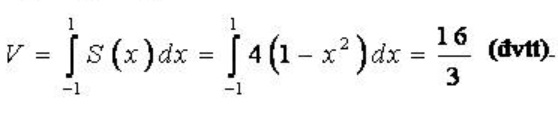
Ví dụ 2: Tính thể tích khối lăng trụ, biết diện tích đáy bằng B và chiều cao bằng h

Lời giải

Ta có hình vẽ như sau:

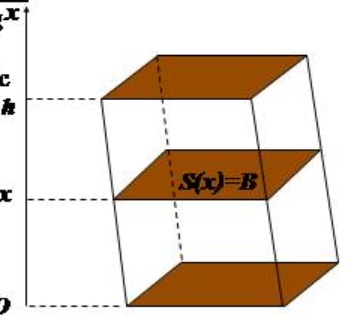
Chọn trục Ox song song với đường cao của khối lăng trụ còn lại 2 đáy sẽ nằm trogn 2 mặt phawngt vuông góc với Ox tại x=0 và x=h

Áp dụng công thức thể tích vật thể ta có

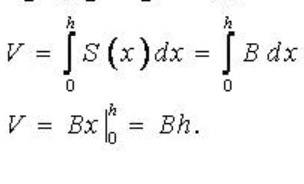
Thế tích các khối tròn xoay trong ứng dụng tích phân

1. Hình phẳng quay quanh trục hoành

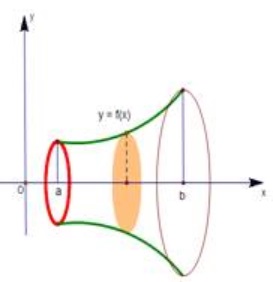
Hình phẳng được giới hạn bởi đồ thị của hàm số y=f(x) không âm và liên tục trên đoạn [a;b], trục Ox và hai đường thẳng x=a, x=b quay quanh trục Ox tạo thành một khối tròn xoay.

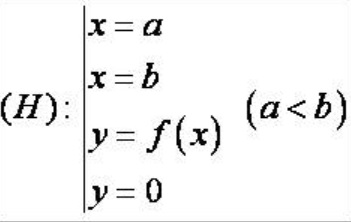
Thế tích của khối tròn xoay là :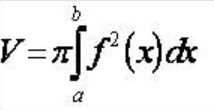

2. Hình phẳng quay trục tung

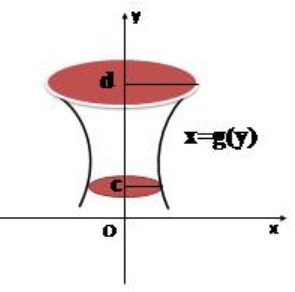
Hình phẳng được giới hạn bởi đồ thị của hàm số x=g(x) không âm và liên tục trên đoạn [c;d], trục Oy và hai đường thẳng y=a, y=b quay quanh trục Oy tạo thành một khối tròn xoay.

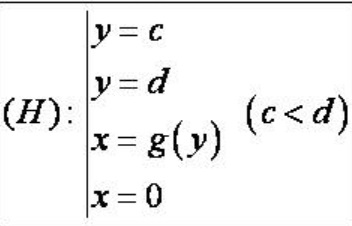
Khi H quay quanh Oy ta có công thức tính V như sau:

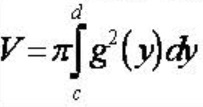
Ví dụ 1: Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường sau quay quanh trục Ox ( trục hoành)

1. x=0, x=п, y= cosx, y=0
2. y = 1 - x^2 , y=0

Lời giải

a) Áp dụng công thức ta có:

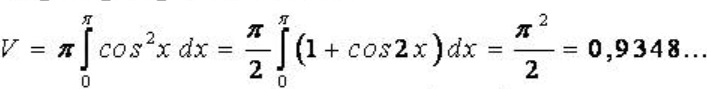
b) Phương trình hđgđ của đồ thị hai hàm số: 1-x^2 = 0 ⇔ x = 1 và x=-1

Do đó H chính là hình phẳng giới hạn bởi các đường x=-1 và x=1, y= 1-x^2 , y=0 Áp dụng công thức ta có:

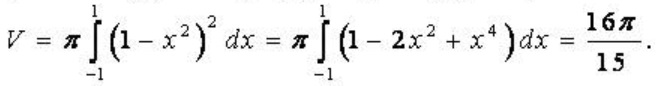
Ví dụ 2: Cho hình phẳng ( B) giới hạn bởi các đường y=1, y=8, x= √2y và trục Oy. Tính thể tích của khối tròn xoay tạo thành khi quay hình (B) quay trục tung.

Lời giải

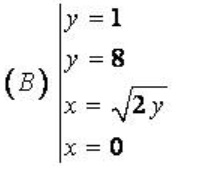
Áp dụng công thức ta được:

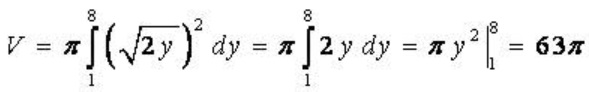
Ví dụ 3: Cho hình phẳng A giới hạn bởi đường cong có phương trình x-y^2 = 0 và đường thằng y = 2 ; x=0 . Tính thể tích khối tròn xoay tạo thành khi quay A.

a. Quay trục hoành

b. Quay trục tung

Lời giải

Ta có hình vẽ:

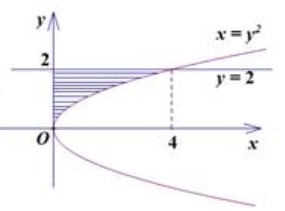
a) hoành độ giao điểm của đường cong x - y^2 = 0 đường thẳng y = 2 là nghiệm của phương trình: √x = 2 ⇔ x=4 .

Gọi V là thể tích khối tròn xoay tạo thành khi quay A quanh trục hoành thì dễ thấy

V= V1 - V2 trong đó:

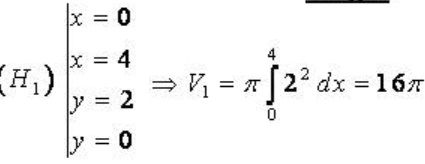
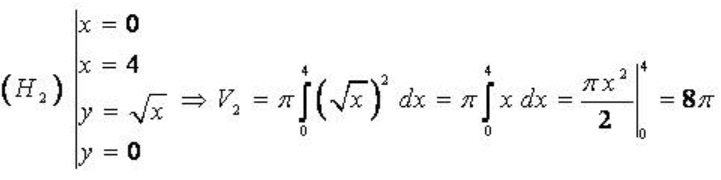
Vậy V= V1 - V2 = 16п - 8п= 8п

Tình quãng đường đi được

Chú ý: Kí hiệu s(t); v(t); a(t) lần lượt là quãng đường vận tốc và gia tốc của vật . Khi đó ta sẽ mối liên hệ:

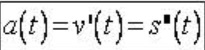
Ví dụ 1: Một ôtô đang chạy với vận tốc 36km/h thì tăng tốc chuyển đông nhanh dần đều với gia tốc : a(t) = 1+ t/3 (m/s^2) . Tính quãng đường mà oto đi được sau 6s kể từ khi bắt đầu tăng tốc.

Lời giải

Đổi 36 km/h = 10 m/s chọn mốc thời gian là lúc oto bắt đầu tăng tốc vận tốc của vật:

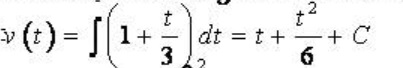
Theo bài ra ta có:

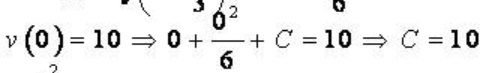
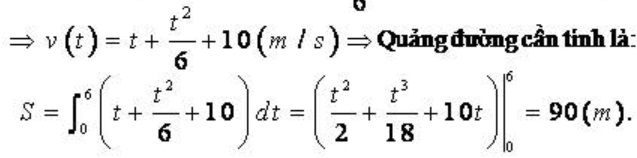
Kết luận

Trên đây là bài viết về ứng dụng tích phân trong hình học mà thayphu.net muốn chia sẻ đến các em học sinh. Hy vọng rằng dạng bài tập này sẽ giúp các bạn có thể dành được điểm cao hơn trong ngày thi tốt nghiệp. Chúc các bạn thành công và đỗ đại học nhé!