Lý thuyết Tọa độ trong không gian và bài tập áp dụng

Tọa độ trong không gian là một khái niệm quan trọng trong Toán 12. Cùng tìm hiểu kiến thức chung, tính chất, ứng dụng và các bài tập vận dụng của dạng toán này nhé.

Hệ tọa độ không gian ba chiều (hay tọa độ ba chiều) được sử dụng để biểu diễn vị trí của một điểm trong không gian ba chiều. Nó bao gồm ba trục vuông góc với nhau: trục x, trục y và trục z. Mỗi điểm trong không gian được xác định bởi một bộ ba giá trị số (x, y, z), trong đó x là hoành độ, y là tung độ và z là cao độ của điểm đó.

Hệ tọa độ trong không gian có thể giúp chúng ta biểu diễn các đối tượng và diễn tả vị trí của chúng dưới dạng các bộ số. Bằng cách sử dụng hệ tọa độ này, ta có thể thực hiện các phép toán hình học, tính toán khoảng cách và các phép biến đổi khác trong không gian. Trong bài viết này, hãy cùng Thayphu tìm hiểu định nghĩa, tính chất, và các ứng dụng của tọa độ trong không gian nhé.

Kiến thức chung cần nhớ của tọa độ trong không gian

Tọa độ không gian là gì?

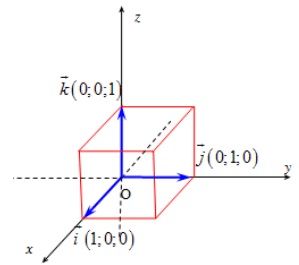
Trong không gian ta có ba trục tọa độ chung gốc O và đôi một vuông góc với nhau được gọi là hệ tọa độ Oxyz.

Trong đó:

• O (0; 0; 0) gọi là gốc tọa độ
• Ox: trục hoành
• Oy: trục tung
• Oz: trục cao
• (Oxy); (Oxz); (Oyz) có đôi một vuông góc với nhau

Ngoài ra:

Các trường hợp đặc biệt cần lưu ý

• A ∈ Ox ⇔ A(x; 0; 0)

A ∈ Oy ⇔ A(0; y; 0)

A ∈ Oz ⇔ A(0; 0; z)

• B ∈ (Oxy) ⇔ B(x; y; 0)

B ∈ (Oyz) ⇔ B(0; y; z)

B ∈ (Oxz) ⇔ B(x; 0; z)

• Tọa độ điểm: OM=x.i+y.j+z.k ⇔ M(x; y; z)

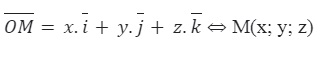
• Tọa độ vectơ: a=(a1.i+a2.j+a3.k ⇔ a=(a1; a2; a3)

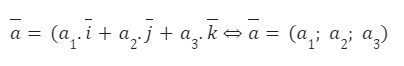
Tính chất

Cho a = (x1; y1; z1), b = (x2; y2; z2) và số k tùy ý, ta có:

1. Tổng, hiệu của 2 vectơ là 1 vectơ

vecto a + b = (x1 + x2; y1 + y2; z1 + z2)

vecto a - b = (x1 - x2; y1 - y2; z1 - z2)

2. Tích của vectơ với 1 số thực cũng là 1 vectơ

k.a = k.(x1; y1; z1) = (kx1; ky1; kz1)

3. Vectơ không có tọa độ là : 0 (0; 0; 0)

4. Hai vectơ bằng nhau có tọa độ tương ứng cũng bằng nhau

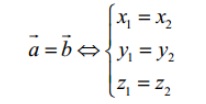
5. Tích vô hướng của 2 vectơ

a.b = x1.x2 + y1.y2 + z1.z2

6. Góc giữa 2 vectơ chính là tích vô hướng của chúng chia tích độ dài

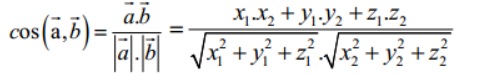
Ứng dụng

• Tính khoảng cách giữa hai điểm: Sử dụng công thức tính khoảng cách Euclid, học sinh có thể tính được khoảng cách giữa hai điểm trong không gian. Điều này có ứng dụng trong việc xác định khoảng cách giữa hai đối tượng, đo đạc khoảng cách hay tính toán trong các bài toán hình học.
• Xác định góc giữa các đường thẳng và mặt phẳng: Sử dụng tọa độ của các điểm trên đường thẳng và mặt phẳng, chúng ta có thể dễ dàng tính được góc giữa chúng. Ứng dụng trong việc xác định tính song song, vuông góc hay góc giữa các đường thẳng, mặt phẳng trong không gian.
• Tìm giao điểm của các đường thẳng và mặt phẳng: Sử dụng tọa độ, ta có thể tìm được giao điểm của hai đường thẳng hoặc giao điểm của đường thẳng với mặt phẳng. Tính chất này vô cùng hữu ích trong việc giải các bài toán về giao điểm, cắt nhau hay tiếp xúc giữa các hình học không gian.
• Định hướng và vectơ: Tọa độ trong không gian cũng cho phép xác định hướng và biểu diễn các vectơ. Giúp chúng ta dễ dàng tính toán độ dài, hướng và các phép toán vectơ như cộng, trừ hay nhân vô hướng của các vectơ trong không gian.

Bài tập vận dụng của các dạng toán tọa độ

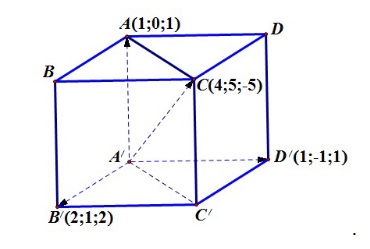
Bài 1: Cho hình hộp ABCD.A’B’C’D’, trong không gian với hệ tọa độ Oxyz, Biết A(1; 0; 1), B’(2; 1; 2), D’(1; -1; 1), C(4; 5; -5). Gọi tọa độ của đỉnh A’(a; b; c). Khi đó 2a + b + c bằng?

1. 7
2. 2
3. 8
4. 3

Gợi ý lời giải

Chọn D.

Ta có tọa độ của các vectơ như sau:

A’D’ = (1-a; -1-b; 1-c)

A’B’ = (2-a; 1-b; 2-c)

A’A = (1-a; -b; 1-c)

A’C = (4-a; 5-b; -5-c)

Theo quy tắc hình hộp, ta có A’C = A’B’ + A’D’ + A’A

⇔ (4-a; 5-b; -5-c) = (4-3a; 2-3b; 3-3c)

4-a = a-3a

⇔ 5-b = 2-4b

-5-c = 3-3c

⇔ a = 0; b = -1; c = 4

Vậy 2a + b + c = 3

Bài 2: Trong không gian với hệ tọa độ Oxyz, điểm nào sau đây thuộc mặt phẳng (Oxy)

1. N(1; 0; 2)
2. P(0; 1; 2)
3. Q(0; 0; 2)
4. M(1; 2; 0)

Gợi ý lời giải

Chọn D

Phương trình mặt phẳng (Oxy) có z = 0. Kiểm tra tọa độ các điểm ta thấy D ∈ (Oxy).

Bài 3: Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A(1; 2; -1), B(-3; 4; 3); C(3; 1; -3), tìm số điểm D sao cho 4 điểm A, B, C, D là 4 đỉnh của 1 hình bình hành là

1. 2
2. 1
3. 3
4. 0

Gợi ý lời giải

Chọn D

Ta có độ dài của các vectơ như sau

AB = (-4; 2; 4), AC = (2; -1; -2)

Dễ thấy AB = -2AC nên hay vecto AB, AC cùng phương do đó ba điểm A, B, C thẳng hàng.

Khi đó không có điểm D nào để bốn điểm A, B, C, D là bốn đỉnh của 1 hình bình hành.

Vậy không có điểm nào thỏa mãn yêu cầu bài toán.

Bài 4: Trong không gian cho các vectơ a, b, c không đồng phẳng thỏa mãn (x-y).a + (y-z).b = (x+z-2).c. Tính T = x + y + z.

1. 3
2. 1
3. 2
4. 3/2

Gợi ý lời giải

Chọn A

Vì các vectơ a, b, c không đồng phẳng nên:

x - y = 0

y - z = 0

x + z - 2 = 0

⇔ x = y = z = 1

Vậy T = x + y + z = 3.

Bài 5: Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(a,b,c); B(m;n;p). Điều kiện để A, B nằm về hai phía của mặt phẳng (Oyz) là

1. am < 0
2. c + p < 0
3. cp < 0
4. bn < 0

Gợi ý lời giải

Chọn A

Ta có phương trình mặt phẳng (Oyz) là x = 0

Do đó A và B nằm về hai phía của mặt phẳng (Oyz) khi và chỉ khi hoành độ của điểm A và hoành độ của điểm B trái dấu. Điều này xảy ra khi am < 0.

Kết luận

Tọa độ trong không gian là một dạng toán quan trọng, đặc biệt là trong chương trình toán 12 khi mà đây là một trong những dạng toán sẽ xuất hiện ở những câu mức 7-8+ trong đề thi THPT QG. Vì vậy, các bạn học sinh cần ôn tập thật kỹ, nắm chắc phương pháp giải dạng toán này để dễ dàng giải quyết chúng nhé.