Cách tìm số phức Z thỏa mãn điều kiện cho trước đạt điểm cao

Hướng dẫn tìm số phức z thỏa mãn điều kiện cho trướcm, giúp học sinh ôn tập và tìm ra giá trị của số phức z thỏa mãn mọi điều kiện.

Tìm số phức Z thỏa mãn điều kiện cho trước là dạng toán phổ biến được áp dụng ở nhiều bài thi tốt nghiệp. Các em chỉ cần biết điều kiện cho trước và tìm ra số phức z để thỏa mãn được điều kiện đó. Vậy điều kiện là gì? Hãy cùng thayphu tìm hiểu và giải quyết vấn đề này qua bài viết sau đây nhé!

Khái niệm số phức Z thỏa mãn điều kiện cho trước

Khái niệm số phức Z thỏa mãn điều kiện cho trước.

Để giải được các dạng bài tập về tìm số phức Z thỏa mãn điều kiện cho trước. Đòi hỏi các em học sinh phải hiểu hết các khái niệm ở bản về số phức để từ đó làm nền tảng giải được những phần khó hơn.

Cho số phức z có dạng z= a+bi với a,b ε R

Trong đó:

a: là phần thực

b: là phần ảo

i : đơn vị thỏa mãn i^2 = -1

Đặc biệt

Số phức liên hợp :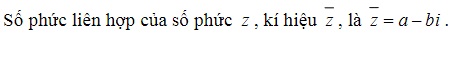

Modun số phức :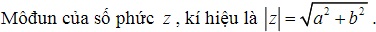

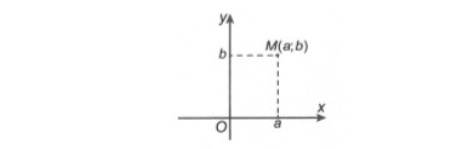
Biểu diễn hình học số phức: Trên mặt phẳng tọa độ Oxy , mỗi số phức z = a + bi , a;b thuộc R được biểu diễn bởi điểm M( a; b) . Ngược lại, mỗi điểm M( a; b) biểu diễn duy nhất một số phức là z=a+bi

Cách tìm số phức z thỏa mãn điều kiện cho trước

Khi đã hiểu cơ bản về định nghĩa số phức thì phương pháp để giải dạng toán này cũng không hề khó khăn gì. Các em chỉ cần áp dụng là có thể bài toán một cách nhanh chóng:

Cho hai số phức z1 = a + bi và z2 = a2 + b2i thì:

⇔ z1 + z2 = (a + a1) + (b + b2)i

⇔ z1 - z2 = (a

- a1) + (b - b2)i

z1 = z2 khi và chỉ khi a = a1 và b = b1

Các dạng bài tập về tìm số phức z thỏa mãn điều kiện cho trước

Tìm số phức z thỏa mãn điều kiện cho trước cũng sẽ có các dạng bài tập khác nhau. Mỗi dạng sẽ có cách tính khác nhau vậy nên khi các em xem và áp dụng sẽ dành được điểm tuyệt đối

Dạng 1: tìm số thực x,y thỏa mãn điều kiện cho trước

Ví dụ: Tìm số thức x,y thỏa mãn điều kiện .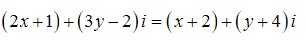

Lời giải:

Ta có :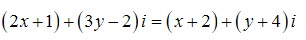

⇔ 2x+1 = x+2

3y-2 = y+4

=> x= 1 và y=3

Vậy x, y lần lượt là ( 1;3)

Dạng 2: Cho số phức thỏa mãn điều kiện tính a,b

Ví dụ1: Cho số phức z= a+bi thỏa mãn điều kiện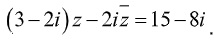

Tính tổng a+b

Trả lời

ta có z= a+bi =>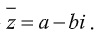

Theo đề bài ta có

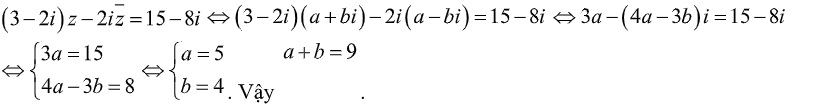
Ví dụ 2: cho số phức z=a+bi, thỏa mãn điều kiện 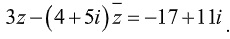. Tính ab

Lời giải

ta có z= a+bi =>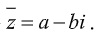

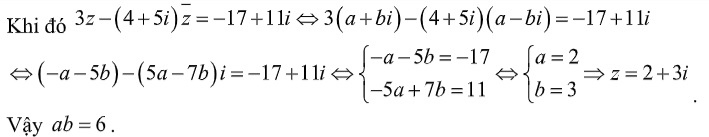
Dạng 3: Cho số phức thỏa mãn tìm modun số phức

Ví dụ: Cho số phức z thỏa mãn 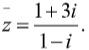tính modun của số phức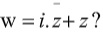

Lời giải

Ta có :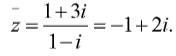

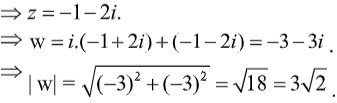
Ví dụ: Cho số thực z=a+bi thỏa mãn điều kiện 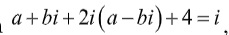Với i là đơn vị ảo. Tính modun của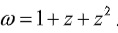

Lời giải

Ta có :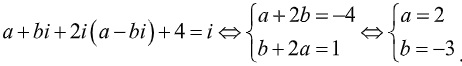

=> z=2-3i

Do đó :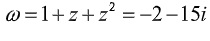

Vậy: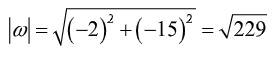

Dạng 4: Tìm số phức z thỏa mãn điều kiện là số thực

Ví dụ: Tìm số phức z thỏa mãn 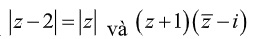là số thực

Lời giải

⇔

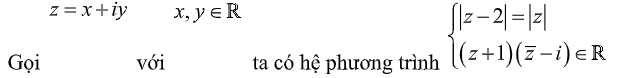
⇔ x= 1 và (-x-1)(y+1) + xy = 0

=> x=1 và y=-2

Dạng 5: Tìm số phức thỏa mãn điều kiện là số thuần ảo

Ví dụ: Có bao nhiêu số phức z thỏa mãn 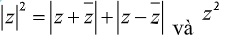là số thuần ảo

Lời giải

Gọi số phức z=a+bi

=> ta có ⇔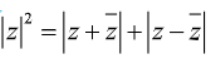

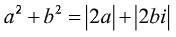
a^2 + b^2 = 2|a| + 2|b| (1)

Theo đề bài ta có z^2 = ( a+bi)^2 = a^2 - b^2 + 2abi là số thuần ảo

=> a^2 - b^2 = 0 ⇔ a= + - b

Từ đây ta xét các trường hợp sau:

Trường hợp 1: a=b thay vào (1) ta được:

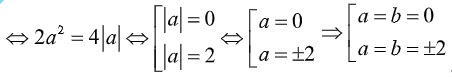
Trường hợp 2: a= -b thay vào (1) ta được:

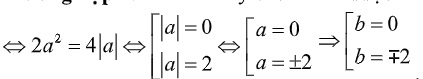
Vậy bài sẽ có 5 phương trình thỏa mãn điều kiện :

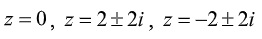
Dạng 6 : Biểu diễn hình học thỏa mãn điều kiện tìm số phức

Ví dụ: Trong mặt phẳng phức, cho 3 điểm ABC lần lượt là điểm biểu diễn của các số phức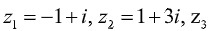. Biết tam giác ABC vuông cân tại A và z3 có phần thực dương. Khi đó tọa độ điểm C là bao nhiêu.

Lời giải

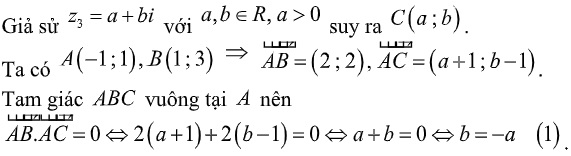
Tam giác ABC cân tại A nên AC=AB ⇔ AC^2 = AB^2

⇔ (a+1)^2 + (b-1)^2 = 8 (2)

Thể vào (1) và (2) ta có :

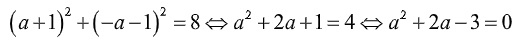
=> a=1 và a=-3

Vì a>0 nên a=1 và b=-1 => tọa độ điểm C là ( 1;-1)

Kết luận

Trên đây là phương pháp tìm số phức z thỏa mãn điều kiện cho trước. Về cơ bản thì số phức rất đa dạng về bài tập và phương pháp tính. Vậy nên hy vọng bài viết này sẽ giúp ích cho các em đạt được số điểm cao. Đừng quên truy cập trang web của thayphu để hiểu hơn về bài học nhé!