Cách tìm m để hàm số có cực đại, cực tiểu và bài tập

Tìm m để hàm số có cực đại, cực tiểu là kiến thức trọng tâm trong toán học. Yêu cầu giải phương trình và kiểm tra tính chất của các điểm cực trị để tìm m.

Trong giải tích, việc tìm cực đại và cực tiểu của hàm số là một bài toán quan trọng và thường xuyên được áp dụng. Hôm nay, chúng ta sẽ cùng tìm hiểu về việc tìm m để hàm số có cực đại, cực tiểu. Bài toán có thể được giải quyết thông qua phương trình đạo hàm bằng 0 và kiểm tra tính chất của các điểm cực trị. Hãy cùng Thayphu khám phá chi tiết trong bài viết này.

Hàm số đạt cực đại cực tiểu khi nào?

Trước khi tìm hiểu về kiến thức tìm m để hàm số có cực đại, cực tiểu thì các em học sinh phải biết được khi nào hàm số đạt cực đại cực tiểu.

Cho hàm số f(x) ta có:

• Xo thuộc D được gọi là điểm cực đại của f(x) nếu tồn tại một khoảng (a;b) sao cho Xo thuộc (a;b) và f(Xo) > f(x) ∀x ∈ (a,b)∖{xo}
• Nếu tồn tại một khoảng (a;b) ⊂ D sao cho x1 ∈ (a;b) và f(x1) < f(x) với mọi x ∈ (a,b) trừ x0, thì điểm x1 ∈ D được xem là điểm cực tiểu của hàm số f(x).

Cực đại và cực tiểu được gọi là cực trị. Khi một điểm xo là cực trị của hàm số f(x), ta nói rằng hàm số f(x) đạt cực trị tại điểm xo.

Tìm m để hàm số đạt cực đại, cực tiểu

Khi tìm m để hàm số đạt cực đại , cực tiểu sẽ có 2 trường hợp chính về hàm số. Đó là tìm m của hàm bậc 3 và hàm trùng phương. Xét 2 trường hợp này sẽ giúp các em có thể giải bài toán đơn giản hơn.

Tìm m để hàm bậc 3 có cực trị

Đối với hàm bậc 3, ta có thể làm trắc nghiệm như sau:

• Khi hàm số đạt cực tiểu tại x = xo

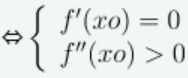
• Khi hàm số đạt cực đại tại x=xo

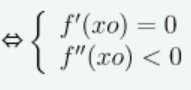
Để có thể xác định rõ hơn ta có bảng biến thiên sau:

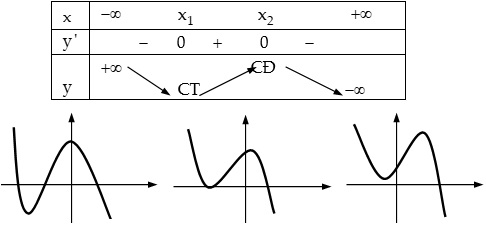
Tìm m để hàm trùng phương có cực trị

Xét hàm số y= ax^4 + bx^2 + c ( a khác 0) Có đạo hàm là y’= 4ax^3 + 2bx

Đồ thị hàm số có 3 điểm cực trị khi và chỉ khi y’=0 có đúng một nghiệm => ab>= 0

Đồ thị hàm số có một cực tiểu và 3 cực đại hoặc 3 cực tiểu và 1 cực đại nằm trên trục tung

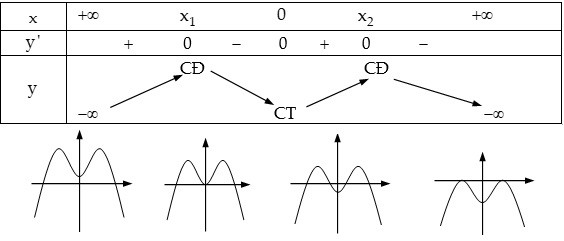
Cách tìm m để hàm số đạt cực đại cực tiểu

Để tim m thì các bạn cần phải dựa vào yêu cầu của để bài đưa ra. Tuy nhiên cách để tìm m thì đều giống nhau và có các bước như sau:

• Bước 1: Tìm đạo hàm của hàm số
• Bước 2: Tìm ẩn m suy ra nghiệm
• Bước 3: Từ kết quả để xác định hàm cực đại hay cực tiểu

Bài tập vận dụng

Bài 1: Tìm giá trị của m sao cho hàm số f(x) 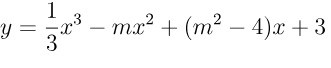đạt giá trị cực đại tại điểm x = 3.

Lời giải:

Đạo hàm của hàm số y’= x^2 - 2mx + m^2 - 4 => y”= 2x -2m

Theo đề bài cho hàm số đạt cực đại với x= 3

y’(3) = 0 ⇔ m^2 - 6m + 5 = 0

=> m= 1 và m=5

Khi m = 1⇔ y’’ (3) = 2.3 – 2.1 = 4 > 0 suy ra x = 3 là điểm cực tiểu.

Khi m = 5 ⇔ y’’ (3) = 2.3 – 2.5 = -4 < 0 suy ra x = 3 là điểm cực đại.

Bài 2: Có một hàm số y = ax^ 3 + x^ 2 – 5x + b có giá trị cực tiểu tại x = 1 và giá trị cực tiểu là 2. Giá trị của biểu thức H = 4a – b là bao nhiêu?

Lời giải:

Đạo hàm của hàm số y’ = 3ax^2 + 2x - 5 => y”= 6ax + 2

Hàm số đạt cực tiểu tại x = 1

⇒ y’ (1) = 0 ⇔ a = 1 Thay a = 1 ta thấy y’’ (1) = 6 + 2 = 8 > 0

Nên x = 1 là điểm cực tiểu.

Ta có: y (1) = 2

⇔ 1 + 1 – 5 + b = 2

⇔ b = 5

Vậy => H = 4. 1 – 5 = -1.

Bài 3: Tìm giá trị của m sao cho hàm số y = x^3 + mx - 1 đạt giá trị cực đại và cực tiểu.

Lời giải:

Nếu hàm số y = x^3 + mx - 1 có cực đại và cực tiểu thì phải thỏa mãn điều kiện Sau:

y' = 0 có hai nghiệm phân biệt

Hay 3x^2 + m = 0 có hai nghiệm phân biệt.

Vì vậy, ta suy ra m < 0.

Bài 4: Biết hàm số f(x) = ax^3 + bx^2 + cx + d đạt cực tiểu tại điểm x = 0, có giá trị f(0) = 0 và đạt cực đại tại điểm x = 1, có giá trị f(1) = 1. Tính giá trị của biểu thức T = a + 2b – 3c + d.

Lời giải:

Hàm số có đạo hàm là f'(x) = 3ax^2 + 2bx + c.

Vì hàm số đạt giá trị nhỏ nhất tại x = 0 và f(0) = 0, và đạt giá trị lớn nhất tại x = 1 và f(1) = 1, ta có thể viết thành hệ phương trình.

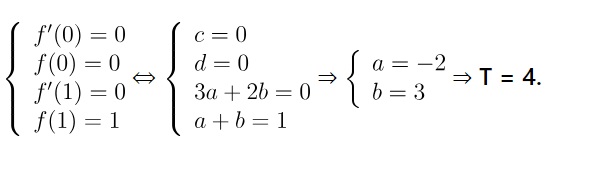
Bài 5: Tìm các giá trị của m để hàm số y = x^3 + (1 – 2m)x^2 + (2 – m)x + m + 2 có điểm cực đại, cực tiểu và hoành độ của điểm cực tiểu nhỏ hơn 1.

Lời giải:

Đạo hàm y’ = 3x^ 2 + 2 (1 – 2m) x + 2 – m cho ta biết đồ thị hàm số sẽ có điểm cực đại và cực tiểu khi có hai nghiệm phân biệt của phương trình đó.

Điều này tương đương với việc:

∆’ = (1 – 2m) ^2 – 3 (2 – m) > 0, hay 4m^2 – m – 5 > 0.

⇔ m<-1 và m> 5/4

Giả sử y' = 0 có hai nghiệm x1 và x2 (với x1 < x2).’

Từ đây ta có bảng biến thiên sau:

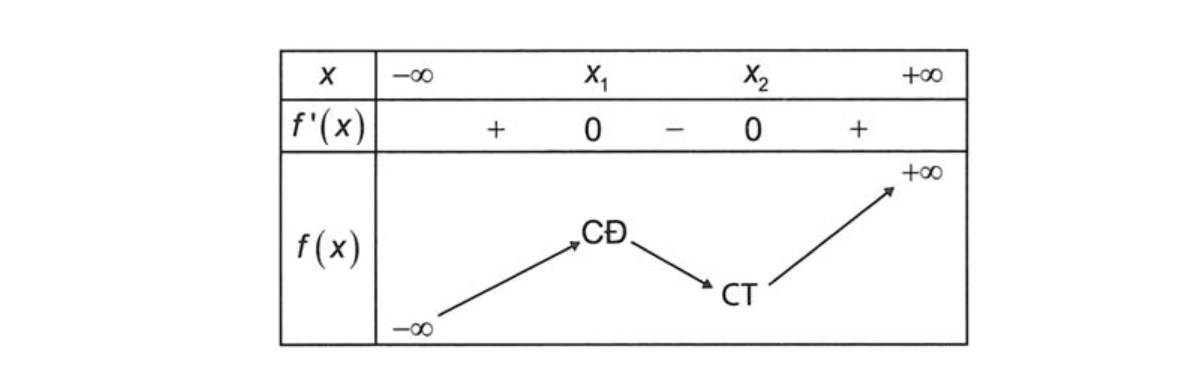
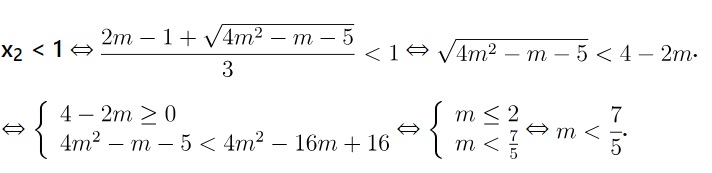
Kết hợp điều kiện có cực trị thì

=> m<-1 và 5/4 <m< 7/5 ( thỏa mãn yêu cầu)

Bài tập tự luyện ở nhà

Kết luận

Tìm m để hàm có cá cực đại cực tiểu đây là một kiến thức tương đối khó. Đòi hỏi các bạn phải có tư duy và sự suy luận trong toán học. Vậy nên hãy nắm vững kiến thức cơ bản vì đấy là nền tảng để tìm tham số m trong dạng bài tập này. Nếu các em đang tìm kiếm những dạng bài học về kiến thức này thì hãy truy cập trang web Thayphu để hiểu hơn nhé!