Các kiến thức Thể tích khối hộp cần nhớ và bài tập vận dụng

Tổng hợp đầy đủ và chi tiết các kiến thức về thể tích khối hộp, khối lập phương, khối hình hộp chữ nhật và các dạng bài tập vận dụng chi tiết hay nhất.

Trong môn Toán hình học không gian, khái niệm và công thức tính thể tích khối hộp là một dạng kiến thức cơ bản nhưng rất quan trọng. Bởi lẽ, các bạn học sinh cần nắm chắc dạng toán này để có thể giải những dạng bài tập nâng cao hơn hoặc những câu ở mức 9+ trong đề thi THPT QG.

Thế nên, để nắm chắc những kiến thức này và giải các bài toán về thể tích khối hộp nhanh nhất và đơn giản nhất, các bạn hãy cùng thayphu khám phá qua bài viết này.

Kiến thức chung cần nắm: Định nghĩa các khối hình hộp

Hình hộp chữ nhật

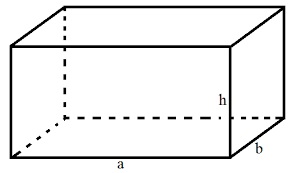
Hình hộp chữ nhật là hình hộp đứng và có đáy là hình chữ nhật. Trong đó, ta gọi a, b, c lần lượt là chiều dài, chiều rộng, chiều cao của hình hộp chữ nhật. Từ đó ta suy ra:

• Đường chéo của hình hộp chữ nhật là:

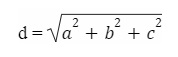
• Diện tích toàn phần của hình hộp chữ nhật là:

S = 2(ab + bc + ca)

• Thể tích hình của hộp chữ nhật là:

V = abc

Hình lập phương

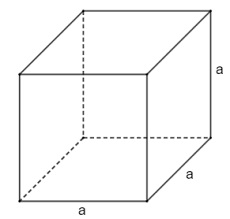
Hình lập phương là hình hộp chữ nhật có 3 kích thước chiều cao, chiều rộng, chiều dài đều bằng nhau. Trong đó, ta gọi a là cạnh của hình lập phương thì suy ra ta có:

• Đường chéo của hình lập phương:

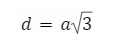
• Diện tích toàn phần khối lập phương:

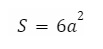
• Thể tích của khối lập phương:

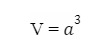
Hình hộp

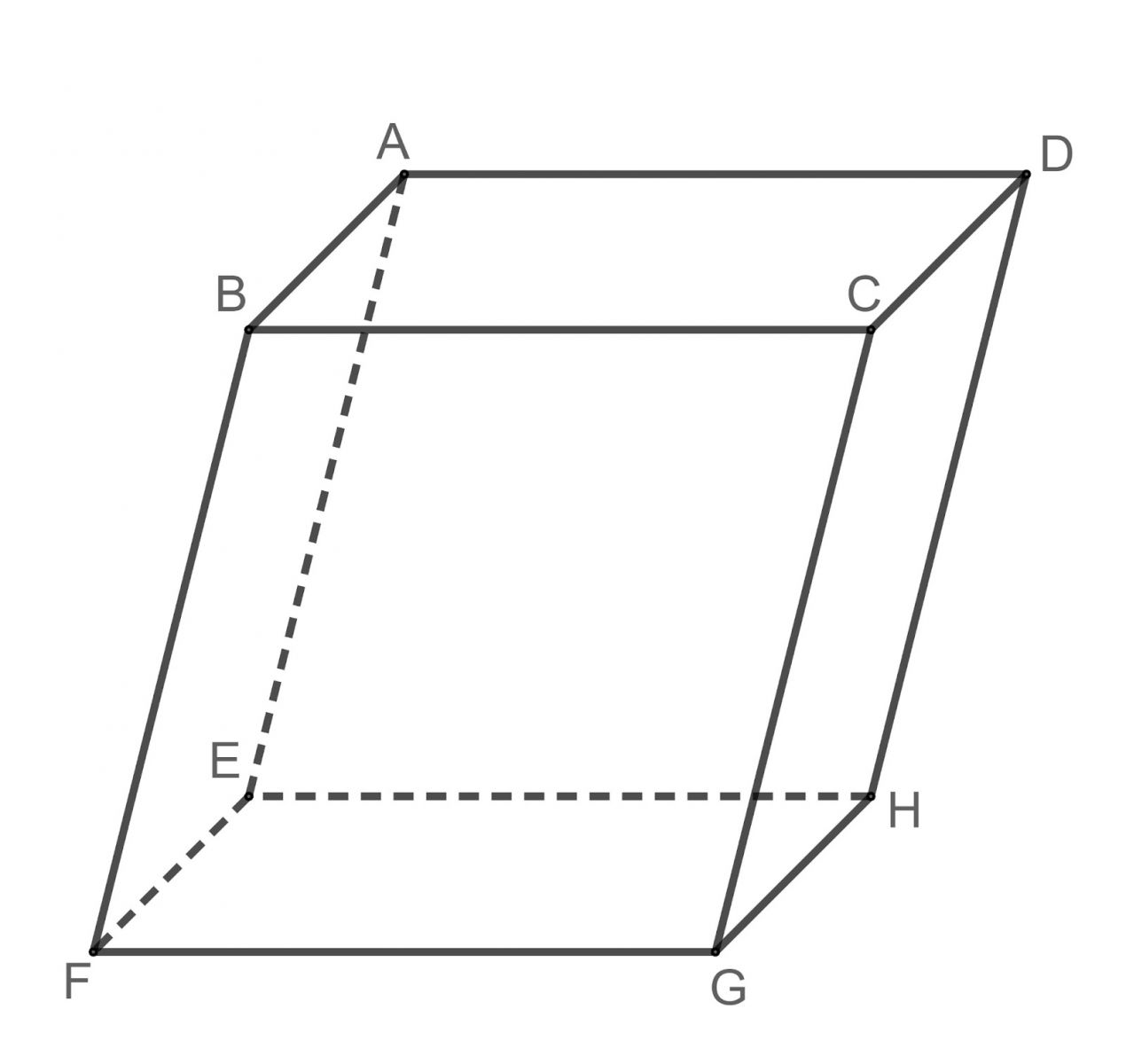
Hình hộp là hình lăng trụ tứ giác có đáy là hình bình hành hoặc hình thoi. Hình hộp có 6 mặt là hình bình hành và có 4 đường chéo đồng quy tại tâm của hình hộp.

Tính chất cơ bản của thể tích khối hộp

• Tính chất tỷ lệ: Thể tích của khối hộp tỷ lệ với sản kích thước của chiều dài, chiều rộng và chiều cao. Tính chất này có nghĩa là khi một trong các kích thước của khối hộp tăng lên một lượng xác định, thể tích cũng tăng lên theo tỷ lệ tương ứng.
• Tính chất hoán đổi: Thể tích của khối hộp không bị thay đổi khi các cạnh của khối hộp đổi chỗ với nhau. Ví dụ như, nếu ta hoán đổi chiều dài và chiều rộng của khối hộp, thể tích vẫn giữ nguyên.
• Tính chất biến đổi tỷ lệ: Nếu ta thay đổi tỷ lệ của khối hộp theo một hệ số nhất định, thì thể tích của khối hộp mới sẽ tăng hoặc giảm theo bình phương của hệ số tỷ lệ đó. Ví dụ, nếu ta nhân các kích thước của khối hộp với một hệ số tỷ lệ là 2, thì thể tích của khối hộp mới sẽ là 2^3 = 8 lần thể tích ban đầu.

Cách tính thể tích khối hộp

• Cách 1: Ta tính thể tích của khối hộp bằng diện tích đáy khối hộp nhân chiều cao của khối hộp đó.
• Cách 2: Trong không gian có gắn hệ trục tọa độ Oxyz thì để có công thức tính thể tích khối hình hộp ABCD.A’B’C’D’, ta có thể dựa vào tích vô hướng, tích có hướng của các vectơ như sau:

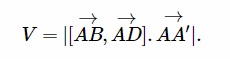
Để chứng minh cho công thức trên, ta có bài tập vận dụng như sau:

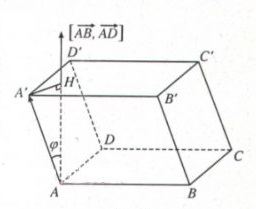
Ta có ABCD.A’B’C’D’ là hình hộp với chiều cao h = AH, diện tích đáy hình bình hành là S và góc hợp bởi hai vectơ AA’ và [AB, AD]. Tính thể tích của hình hộp đã cho.

Gợi ý lời giải:

Dựa vào công thức tính thể tích của hình hộp, ta có:

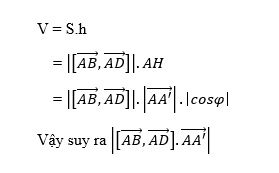
Bài tập vận dụng

Bài tập 1: Hình hộp chữ nhật ABCD.A’B’C’D’có AB = 2cm, AD = 3cm, AC’ = 7cm. Hãy tính thể tích khối hộp ABCD.A’B’C’D’.

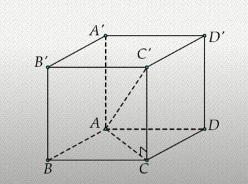
Gợi ý lời giải:

Ta có: AC = √(AB^2 + AD^2) =(√4 + 9) = √13

CC’ = √(AC’^2-AC^2) = 6

Vậy thể tích của hình hộp chữ nhật ABCD.A’B’C’D’ = 2.3.6 = 36

Bài tập 2: Hình lập phương ABCD.A’B’C’D’ có diện tích tam giác ACD’ bằng a^2√3. Hãy tính thể tích của khối lập phương ABCD.A’B’C’D’.

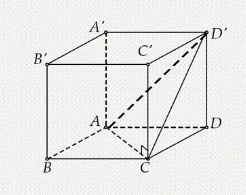
Gợi ý lời giải:

Theo tính chất của khối lập phương thì ta có đường chéo các mặt của hình lập phương là bằng nhau.

Gọi cạnh của hình lập phương là x

Ta có AC = AC’ = CD’ = x√2

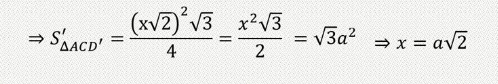
Vậy thể tích của khối lập phương ABCD.A’B’C’D’ đã cho = x^2 = 2√2(a^2).

Bài tập 3: Hình hộp chữ nhật ABCD.A’B’C’D’ có diện tích các mặt ABCD, BCC’B’, CDD’C’ lần lượt là 2a^2, 3a^2,6a^2. Hãy tính thể tích khối hộp chữ nhật ABCD.A’B’C’D’.

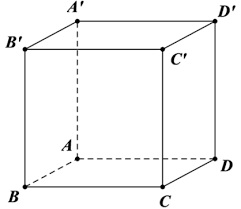
Gợi ý lời giải:

Ta có:

Diện tích mặt ABCD = 2a^2 => AB.BC = 2A^2 (1)

Diện tích mặt BCC’B’ = 3a^2 => BC.BB’ = 3a^2 (2)

Diện tích mặt CDD’C’ = 6a^2 => CD.CC’ = 6a^2 => AB.BB’ = 6a^2 (3)

Từ (1), (2), (3) suy ra => (AB.BC.BB’)^2 = 36a^6 => AB.BC.BB’ =6a^3

Kết luận

Như vậy, qua bài viết này thayphu.net đã giới thiệu đến các bạn học sinh khái niệm của các dạng hình hộp và công thức tính thể tích của chúng. Song song đó là các bài tập vận dụng mẫu về dạng toán tính thể tích này. Đây được coi là những kiến thức nền tảng cơ bản để từ đó chúng ta có thể xây nên những dạng nâng cao hơn. Thông qua việc hiểu và áp dụng công thức tính thể tích của khối hộp, chúng ta có thể sử dụng nó để giải quyết các bài toán liên quan đến hình học và thực tế. Bởi lẽ đây là những kiến thức trọng tâm thường xuyên xuất hiện trong các đề thi quan trọng như kỳ thi THPT QG. Vì vậy các em hãy ôn tập thật kỹ nhé.