Công thức tính thể tích khối chóp và khối lăng trụ

Chia sẻ công thức tính thể tích khối chóp, lăng trụ và các bài tập vận dụng thực tế trong các đề thi đại học hiện nay.

Trong toán học hình học, tính thể tích của các hình học không gian như khối chóp và lăng trụ là một khái niệm quan trọng, các dạng toán này thường xuất hiện trong các đề THPTQG.

Bài viết này, thayphu sẽ cung cấp cho bạn công thức chi tiết để tính thể tích của khối chóp và lăng trụ, kèm theo các bài tập vận dụng thực tế để giúp bạn hiểu rõ hơn về cách áp dụng chúng trong môn Toán hình học Không gian lớp 12.

Công thức tính thể tích khối chóp

Khối chóp là một hình học không gian có đáy là một hình đa giác và các cạnh từ đỉnh của đáy đến một điểm duy nhất trên mặt phẳng nằm ngoài đáy. Để tính thể tích khối chóp, ta có công thức như sau:

V=⅓ x S xh

Trong đó ta có:

• V: là thể tích của khối chóp
• S: là diện tích đáy của khối chóp
• h: là chiều cao của khối chóp (tính từ đỉnh của khối chóp đến mặt đáy)

Công thức tính thể tích lăng trụ

Lăng trụ là một hình học không gian có đáy là một hình tròn và các cạnh từ đỉnh của đáy đến một điểm duy nhất trên mặt phẳng nằm song song với đáy. Để tính thể tích lăng trụ, ta sử dụng công thức sau:

V = S x h

Trong đó ta có:

• V: là thể tích của lăng trụ đó
• S: là diện tích đáy của lăng trụ
• h: là chiều cao của lăng trụ

Ngoài ra, lăng trụ đứng cũng có những dạng hình hộp đặc biệt như hình hộp chữ nhật và hình lập phương. Ta có công thức của 2 dạng này như sau:

• Thể tích khối hình hộp chữ nhật:

V = a x b x c

Trong đó:

• V: là thể tích của hình hộp
• a, b, c: lần lượt là kích thước của các cạnh khối hình hộp chữ nhật

• Thể tích khối lập phương:

V=a3

Trong đó:

• V là thể tích khối lập phương
• a là độ dài của cạnh.

Các bài tập áp dụng

Bài tập tính thể tích khối chóp

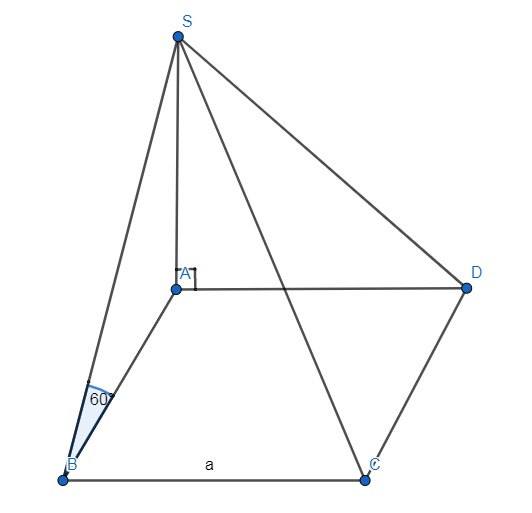
Bài tập 1: Cho một hình chóp S.ABCD có mặt đáy là hình vuông cạnh a. SA vuông góc với mặt phẳng ABCD. Cạnh bên SB hợp với mặt đáy một góc 60 độ. Tính thể tích của khối chóp S.ABCD theo a.

Gợi ý lời giải:

Ta có: SA vuông góc với (ABCD) => SA = h(SA là đường cao của khối chóp)

Dựa vào công thức tính thể tích khối chóp, ta có:

V = ⅓ x S x h

S = a2 (do đáy là hình vuông cạnh a)

• (SB, ABCD) =60 (đề bài)
• SB giao với ABCD tại B
• SA vuông góc (ABCD)

=> góc SBA = 60 độ

Mà tam giác SAB có góc A = 90 độ

=> tan60 = SA/a

Suy ra cạnh SA = a3

Vậy thể tích khối chóp S.ABCD là

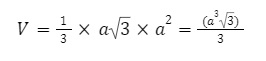
Bài tập 2: Cho khối chóp S.ABCD có ABCD là hình vuông cạnh a. Có tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt phẳng (ABCD). Hãy tính thể tích của khối chóp S.ABCD theo a.

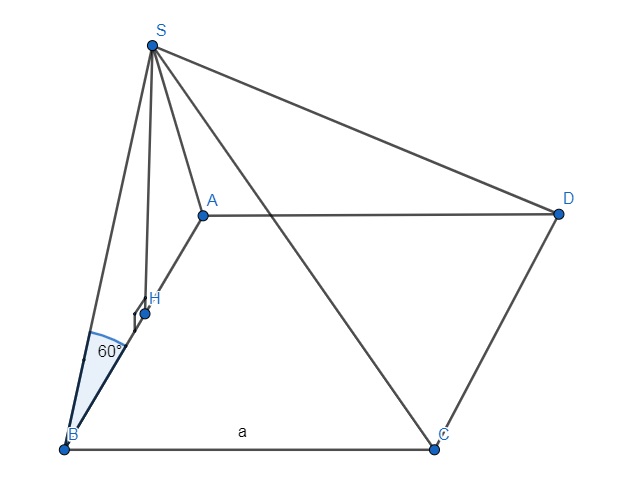
Gợi ý lời giải:

Ta có: (SAB) vuông góc với (ABCD)

• (SAB) giao với (ABCD) tại AB
• Kẻ SH vuông góc AB

=> SH vuông với (ABCD)

Theo ông thức tính thể tích khối chóp, ta có:

V = ⅓ x S x h

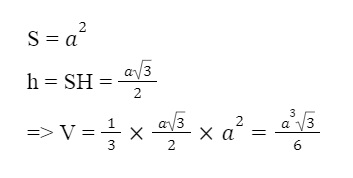
Bài tập luyện tập về tính thể tích khối lăng trụ

Bài tập 1: Cho lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông tại B và BA = BC =1. Cạnh A’B tạo với mặt đáy (ABC) góc 60 độ, hãy tính thể tích khối lăng trụ ABC.A’B’C’.

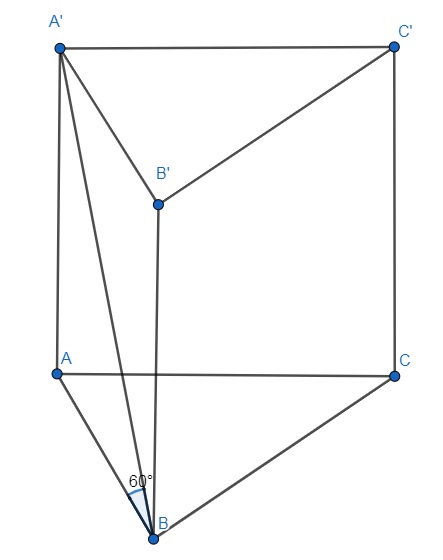
Gợi ý lời giải:

Ta có:

(A’B,ABC) =60 độ

A’B giao với (ABC) = B

Từ A’ có AA’ vuông góc với đáy

=> góc A’BA =60 độ

Dựa vào công thức tính thể tích hình lăng trụ, ta có:

V = S x h

• S = ½ x BA x BC = ½

• Tam giác A’AB, góc A = 90 độ

=> tan60 = h/1 => h = căn 3

Vậy suy ra thể tích của khối lăng trụ ABC.A’B’C’ là:

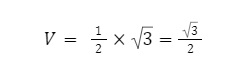
Bài tập 2: Lăng trụ đứng ABC.A’B’C’ có mặt đáy là tam giác vuông cân tại A, cạnh AB= AC=a và AA’=2a. Hãy tính thể tích khối lăng trụ đã cho.

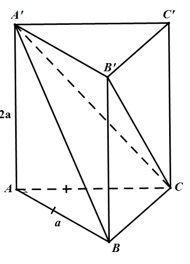
Gợi ý lời giải:

Theo công thức tính thể tích lăng trụ đứng, ta có:

V = S x h

• Chiều cao của lăng trụ là AA’=2a

• S = ½ x ABxAC = ½ .a.a = a^2/2

=> Vậy thể tích của khối lăng trụ ABC.A’B’C’ là V = (a^2/2) x 2a = a^3.

Bài viết Công thức tính thể tích khối chóp và lăng trụ đã cung cấp cho bạn các công thức chi tiết để tính thể tích của khối chóp và lăng trụ, cùng với các bài tập thực tế theo từng dạng khác nhau. Hy vọng rằng thông qua bài viết này, thayphu có thể giúp bạn hiểu thêm về cách tính thể tích của các hình học không gian này và có thể áp dụng chúng thật tốt vào các bài toán trong các đề thi.