Công thức tính thể tích bát diện đều và bài tập áp dụng chuẩn nhất

Lý thuyết cơ bản về khối đa diện, nắm vững công thức tính thể tích bát diện đều toán học lơp 12, kèm bài tập áp dụng

Trong toán hình học lớp 12 chúng ta sẽ bắt gặp nhiều hình ảnh và công thức tính khác nhau. Trong đó thể tích khối bát diện đều là một công thức cơ bản mà bạn cần nắm chắc. Một khí nắm chắc công thức, bạn sẽ dễ dàng hơn trong việc giải toán cũng như áp dụng nó vào thực tế. Vậy nên đừng bỏ qua các thông tin mà thayphu.net chia sẻ dưới đây nhé.

Tóm tắt sơ lược về khối đa diện

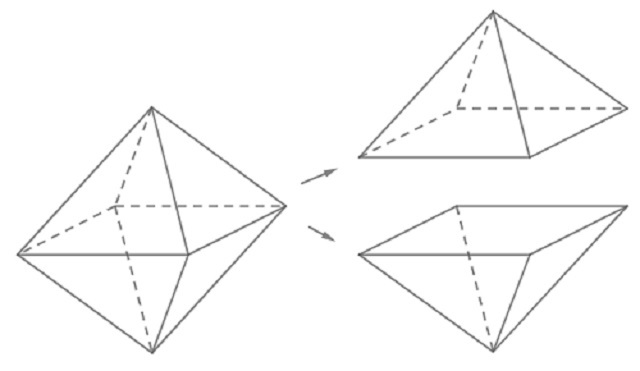
Tóm tắt sơ lược về khối đa diện

Khối đa diện là gì?

Khối đa diện là một hình học không gian bao gồm một số mặt phẳng đa giác được giao nhau tạo thành các mặt và tất cả các cạnh đều là đoạn thẳng. Một khối đa diện được xác định bởi số lượng và hình dạng các mặt và số lượng các cạnh và đỉnh của nó. Các khối đa diện có thể có đặc tính khác nhau tùy thuộc vào số lượng mặt, cạnh và đỉnh của chúng.

Ví dụ về các khối đa diện bao gồm:

• Khối lăng trụ: Là một khối đa diện có 2 đáy là các đa giác đều song song nhau, được kết nối bởi các mặt bên là các hình chữ nhật. Ví dụ: Khối lăng trụ đều, có các đáy là hình vuông đều và các mặt bên là các hình chữ nhật đều.

• Khối tứ diện: Là một khối đa diện có 4 mặt tam giác đều và 4 đỉnh. Các mặt tam giác đều này cắt nhau tại các cạnh của khối. Ví dụ: Khối tứ diện đều, có các cạnh và góc giữa các mặt đều nhau.

• Khối lăng thoi: Là một khối đa diện có 8 mặt là các hình thoi đều và 6 đỉnh. Các mặt thoi này được kết nối bởi các cạnh đều. Ví dụ: Khối lăng thoi đều, có các mặt thoi và các cạnh đều nhau.

Đây là một số ví dụ về các khối đa diện, và có nhiều loại khác nhau tùy thuộc vào số lượng mặt, cạnh và đỉnh của chúng.

Khối đa diện đều là gì?

Khối đa diện đều là một loại khối đa diện có các mặt đều và các cạnh cũng đều và góc giữa các mặt bằng nhau. Các đỉnh của khối đa diện đều nằm trên một lớp cầu tưởng tượng với tâm ở trung tâm của khối. Khối đa

Tính chất của khối đa diện đều bao gồm:

• Các mặt là các hình đa giác đều: Tất cả các mặt của khối đa diện đều có cùng hình dạng và kích thước.

• Các cạnh đều nhau: Tất cả các cạnh của khối đa diện đều có độ dài bằng nhau.

• Các góc giữa các mặt bằng nhau: Góc giữa hai mặt bất kỳ của khối đa diện đều bằng nhau.

• Các đỉnh nằm trên cùng một lớp cầu tưởng tượng: Tất cả các đỉnh của khối đa diện đều nằm trên một lớp cầu tưởng tượng, với tâm ở trung tâm của khối.

Bát diện đều là gì?

Bát diện đều là một trong những khối đa diện đều đơn giản nhất, được tạo thành từ 8 tam giác đều bằng nhau. Nó là một khối đa diện với 8 mặt, 12 cạnh và 6 đỉnh. Bát diện đều có các đặc tính sau:

• Số mặt: 8
• Số cạnh: 12
• Số đỉnh: 6
• Tất cả các mặt đều là tam giác đều
• Các góc giữa hai mặt bằng nhau và đều là góc tù
• Hình bát diện đều thuộc khối đa diện {3;4}
• Mỗi đỉnh của bát diện đều là đỉnh chung của 4 cạnh, 4 mặt

Các đường chéo của bát diện đều bằng nhau và bằng độ dài cạnh nhân căn hai

Bát diện đều là một trong các khối đa diện đặc biệt, được sử dụng trong nhiều lĩnh vực như hình học, vật lý và hóa học. Các tính chất độc đáo của nó đã được áp dụng trong việc tạo ra các phân tử, hạt nhân nguyên tử, các công trình kiến trúc và nhiều ứng dụng khác.

Công thức tính diện tích bát diện đều

Công thức tính diện tích một mặt của bát diện đều:

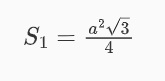
Công thức tính diện tích các mặt của bát diện đều có cạnh là a:

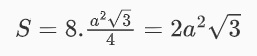
Công thức tính thể tích bát diện đều

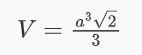
Tính bán kính mặt cầu bát diện đều

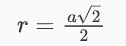
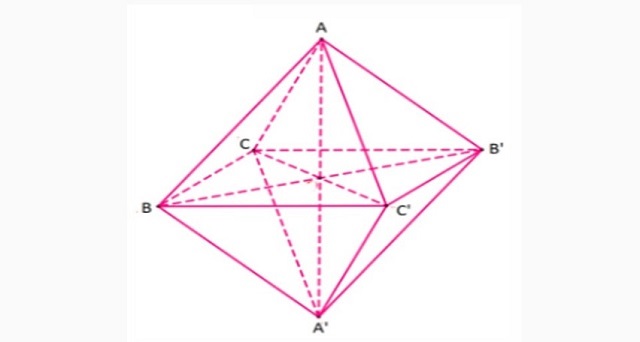
Bán kính mặt cầu bát diện đều

Trục đối xứng lúc này sẽ là điểm nối giữa của hai đỉnh A và A’. Hai điểm này đối xứng qua tâm.

Các ứng dụng của khối bát diện đều có thể bạn chưa biết

• Hóa học: Khối bát diện đều là cấu trúc hình học của nhiều phân tử hữu cơ và vô cơ quan trọng.
• Vật lý: Bát diện đều được sử dụng để mô hình hóa cấu trúc nguyên tử, phân tử và tinh thể. Nó được sử dụng để nghiên cứu cấu trúc và tính chất của các hạt nhân nguyên tử, tinh thể, kim loại và các vật liệu tổng hợp khác.
• Công nghệ: Bát diện đều được sử dụng trong thiết kế và xây dựng các công trình kiến trúc, như các trang trí trên cột, đỉnh tròn và các tòa nhà lớn.
• Giáo dục: Bát diện đều là một trong những hình học đa diện đều đơn giản nhất và được sử dụng trong các chương trình giáo dục để giúp học sinh hiểu về cấu trúc không gian và tính chất của các hình học đa diện khác.

Bài tập áp dụng

1. Thể tích hình bát diện có cạnh là a:

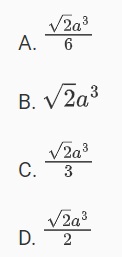
=> Đáp án: C

2. Bát diện đều có bao nhiêu mặt đối xứng?

=> Đáp án: D

3. Bát diện đều có bao nhiêu cạnh?

=> Đáp án: D

4. Diện tích khối bát diện đều có cạnh là 10:

=> Đáp án: D

5. Bát diện đều có bao nhiêu đỉnh:

=> Đáp án: A

Trên đây là toàn bộ thông tin về hình bát diện đều và các công thức liên quan. Các dạng bài liên quan đến khối bát diện đều đều là những câu hỏi ở mức thông hiểu. Vậy nên bạn đừng nên bỏ lỡ những câu hỏi dễ này nhé.