Thể tích hình hộp chữ nhật toán lớp 5 và giải bài tập SGK

Thể tích hình hộp chữ nhật toán lớp 5 bằng độ dài của chiều cao , chiều dài , chiều rộng nhân lại . Hãy cùng chúng tôi tìm hiểu về thể tích cũng như bài tập ứng dụng nhé.

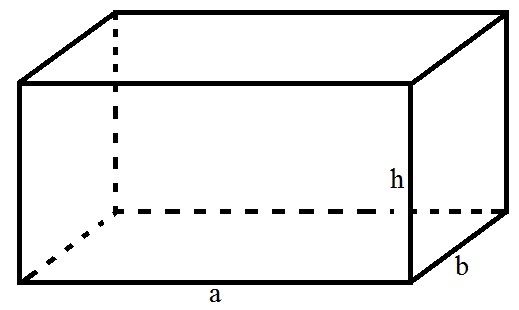
Thể tích của hình hộp chữ nhật là gì? Lý thuyết và bài tập áp dụng

Nó là một trong những hình học cơ bản và thường hay gặp trong toán học cũng như đời sống. Thể tích của hình hộp không chỉ cho biết không gian mà hình hộp chữ nhật có thể chứa đựng, mà còn được ứng dụng thực tế. Trong bài viết này của thayphu chúng ta sẽ cùng tìm hiểu về định nghĩa, công thức tính toán và ứng dụng của thể tích của hình hộp chữ nhật.

Định nghĩa hình hộp chữ nhật toán lớp 5

Chúng là một hình khối ba chiều, được tạo thành bởi 6 mặt phẳng, trong đó:

• Bốn mặt bên (mặt trước, mặt sau, mặt trái, mặt phải) là các hình chữ nhật.
• Hai mặt đối diện (mặt trên và mặt dưới) cũng là các hình chữ nhật.

Ví dụ: Giả sử chúng ta có một hình hộp các kích thước như sau:

Chiều dài (d) = 5 m

Chiều rộng (r) = 3 m

Chiều cao (c) = 2 m

Để tính thể tích của hình hộp này, ta sử dụng công thức:

Thể tích = d x r x c

Thể tích = 5 m x 3 m x 2 m

Thể tích = 30 m³

Ứng dụng thể tích của hình hộp chữ nhật

Hình hộp có nhiều ứng dụng trong thực tế. Dưới đây chúng tôi đã tổng hợp những ứng dụng của hình hộp này:

Tính toán dung tích/khối lượng các sản phẩm/vật dụng

Tính dung tích các hộp, thùng, đóng gói sản phẩm.

Tính khối lượng các sản phẩm có dạng hình hộp chữ nhật như gạch, ximăng, ống nhựa, tấm gỗ, v.v.

Thiết kế và tối ưu hóa không gian

Xác định kích thước cho các không gian như phòng, nhà, kho bãi, container vận chuyển hàng hóa.

Tính toán khối lượng vật liệu xây dựng

Tính khối lượng vật liệu như gạch, bê tông, cốp pha cần thiết để xây dựng các công trình có dạng hình hộp chữ nhật.

Công thức tính thể tích hình hộp chữ nhật toán lớp 5

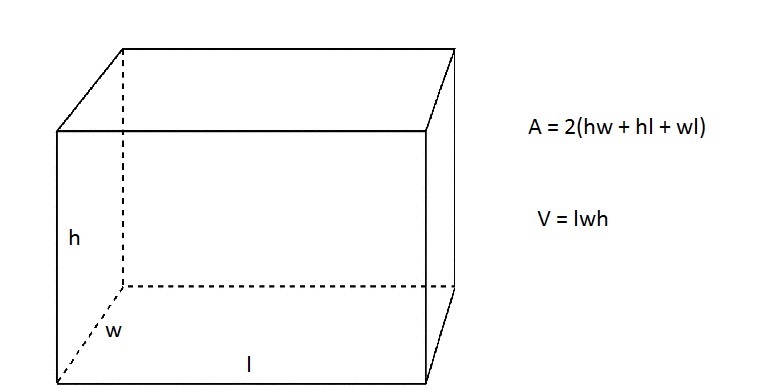
Công thức tính thể tích của hình hộp chữ nhật

Để tính thể tích một hình hộp ta sử dụng công thức sau

Thể tích = chiều dài x chiều rộng x chiều cao

Hoặc viết dưới dạng công thức toán học:

Thể tích = d x r x c

Trong đó:

• d là chiều dài
• r là chiều rộng
• c là chiều cao

Ví dụ: Giả sử chúng ta có một hình hộp với các kích thước:

Chiều dài (d) = 7 m

Chiều rộng (r) = 4 m

Chiều cao (c) = 1 m

Thể tích của hình hộp này sẽ là:

Thể tích = d x r x c

Thể tích = 7m x 4 m x 1 m

Thể tích = 28 m³

Những dạng toán thường gặp về thể tích của hình hộp chữ nhật

Khi nói đến thể tích của một hình hộp ta lại không biết dạng toán nào thuộc hình hộp. Dưới đây chúng tôi đã tổng hợp những dạng toán thường gặp

Dạng 1: Tính thể tích khi biết 3 chiều dài, rộng, cao

Ví dụ: Một hộp chữ nhật có chiều dài 5m, chiều rộng 3m và chiều cao 2m. Hãy tính thể tích của hộp.

Đáp án: Thể tích = 5m x 3m x 2m = 30 m³

Dạng 2: Tìm một trong 3 chiều khi biết thể tích và 2 chiều còn lại

Ví dụ: Một hộp chữ nhật có thể tích 240 m³, chiều dài 12 m và chiều rộng 4 m. Tìm chiều cao của hộp.

Đáp án: Chiều cao = Thể tích / (Chiều dài x Chiều rộng) = 240 m³ / (12 m x 4 m) = 5 m

Dạng 3: Tìm thể tích khi biết một chiều và tỉ lệ giữa các chiều

Ví dụ: Một hộp chữ nhật có chiều dài 6 m, tỉ lệ giữa chiều dài, rộng và cao là 3:2:1. Tính thể tích của hộp.

Đáp án: Chiều rộng = 6 m x 2/3 = 4 m, Chiều cao = 6 m x 1/3 = 2 m

Thể tích = 6 m x 4 m x 2 m = 48 m³

Dạng 4: Tính thể tích khi biết thể tích của một hộp chữ nhật và tỉ lệ các chiều của hộp mới

Ví dụ: Một hộp chữ nhật có thể tích 120 m³, tỉ lệ giữa chiều dài, rộng và cao là 4:3:2. Tính thể tích của hộp mới có tỉ lệ 5:4:3.

Đáp án: Thể tích hộp mới = 120 m³ x (5/4) x (4/3) x (3/2) = 180 m³

Dạng 5: Tính diện tích toàn phần của hình hộp chữ nhật

Ví dụ: Một hộp chữ nhật có chiều dài 4 m, chiều rộng 3 m và chiều cao 2 m. Tính diện tích toàn phần của hộp.

Đáp án: Diện tích toàn phần = 2 x (4 m x 3 m + 4 m x 2 m + 3 m x 2 m) = 2 x (12 m² + 8 m² + 6 m²) = 52 m²

Một số lưu ý khi tính thể tích hình hộp chữ nhật toán lớp 5

Khi tính thể tích của một hộp chữ nhật ta cần lưu ý một số vấn đề sau

Xác định chính xác các kích thước

Cần ghi nhận chính xác chiều dài (l), chiều rộng (w) và chiều cao (h) của hình hộp chữ nhật.

Đơn vị phải thống nhất, ví dụ tất cả đều bằng mét, cm hay inch.

Áp dụng công thức tính thể tích

Thể tích hình hộp chữ nhật = l x w x h

Chú ý đến đơn vị của kết quả

Kết quả tính toán sẽ có đơn vị khối (cubic), ví dụ m³, cm³, inch³.

Cần chú ý đơn vị này khi sử dụng kết quả cho các mục đích cụ thể.

Bài tập áp dụng

Câu 1: Hình hộp chữ nhật có mấy cạnh?

A. 4 cạnh

B. 6 cạnh

C. 8 cạnh

D. 12 cạnh

Đáp án: A. 4 cạnh

Câu2: Công thức tính thể tích của hình hộp chữ nhật là:

A. V = l x w

B. V = l x w x h

C. V = (l + w + h) / 3

D. V = l x w / h

Đáp án: B. V = l x w x h

Câu3: Hình hộp chữ nhật có mấy mặt phẳng?

A. 2 mặt phẳng

B. 4 mặt phẳng

C. 6 mặt phẳng

D. 8 mặt phẳng

Đáp án: C. 6 mặt phẳng

Câu 4: Một hình hộp chữ nhật có chiều dài 5m, chiều rộng 3m và chiều cao 4m. Thể tích của hình hộp đó là:

A. 20 m³

B. 30 m³

C. 60 m³

D. 80 m³

Đáp án: C. 60 m³

Câu 5: Hãy tìm chiều cao của một hình hộp chữ nhật biết thể tích là 120 m³ và diện tích đáy là 40 m².

A. 3 m

B. 4 m

C. 5 m

D. 6 m

Đáp án: B. 4 m

Câu 6: Một hình hộp chữ nhật có chiều dài 6 cm, chiều rộng 4 cm và chiều cao 3 cm. Diện tích toàn phần của hình hộp đó là:

A. 76 cm²

B. 84 cm²

C. 96 cm²

D. 108 cm²

Đáp án: D. 108 cm²

Câu 7: Một hình hộp chữ nhật có thể tích 1000 cm³ và chiều rộng 10 cm. Tính chiều dài của hình hộp đó.

A. 5 cm

B. 10 cm

C. 20 cm

D. 50 cm

Đáp án: C. 20 cm

Câu 8: Hãy tính diện tích xung quanh (diện tích toàn phần trừ đáy) của một hình hộp chữ nhật có chiều dài 8m, chiều rộng 6m và chiều cao 4m.

A. 128 m²

B. 168 m²

C. 208 m²

D. 248 m²

Đáp án: C. 208 m²

Câu 9: Một hình hộp chữ nhật có thể tích 288 cm³ và diện tích toàn phần 192 cm². Tính chiều cao của hình hộp đó.

A. 2 cm

B. 3 cm

C. 4 cm

D. 6 cm

Đáp án: B. 3 cm

Câu 10: Một hình hộp chữ nhật có thể tích 1 m³. Nếu chiều dài tăng 1 m, chiều rộng giảm 1 m và chiều cao không đổi, thể tích mới của hình hộp sẽ là:

A. 1 m³

B. 2 m³

C. 3 m³

D. 4 m³

Đáp án: A. 1 m³

Trên đây là một số thông tin về thể tích hình hộp chữ nhật trong chương trình toán lớp 5. Thayphu.net hi vọng bài viết này đã giúp bạn nắm vững công thức cũng như bài tập này nhé.