Cách viết phương trình mặt phẳng trung trực ăn điểm tuyệt đối

Phương trình mặt phẳng trung trực là dạng toán học giúp xác định vị trí của một điểm trong không gian ba chiều. Dựa trên ba điểm đã biết, với độ chính xác cao.

Phương trình mặt phẳng trung trực một khái niệm quan trọng trong hình học không gian .Được xuất hết ở các bài thi tốt nghiệp cấp 3 và là một kiến thức vô cùng trọng tâm đòi hỏi các em phải biết rõ phương pháp tính. Vậy cách để viết phương trình này như nào? Hãy cùng thayphu tìm hiểu qua bài viết dưới đây của thayphu nhé!

Định nghĩa phương trình mặt phẳng trung trực

Áp dụng công thức viết phương trình

Phương trình mặt phẳng trung trực là phương trình của một mặt phẳng đi qua hai điểm đã cho sao cho đường thẳng nối hai điểm đó là đường vuông góc với mặt phẳng đó.

Phương trình này có dạng: Ax + By + Cz + D=0, trong đó (A, B, C) là vectơ pháp tuyến của mặt phẳng và D là một hằng số.

Nếu mặt phẳng có phương trình Ax + By + Cz + D=0 thì nó sẽ có một vecto pháp tuyến là vectơ n ( A;B;C)

Phương trình tổng quát của mặt phẳng khi đi qua điểm M(x1;y2;z3) và nhận vecto n khác 0 và VTPT là:

A(x-x1)+B(y-y2)+C(z-z3)=0

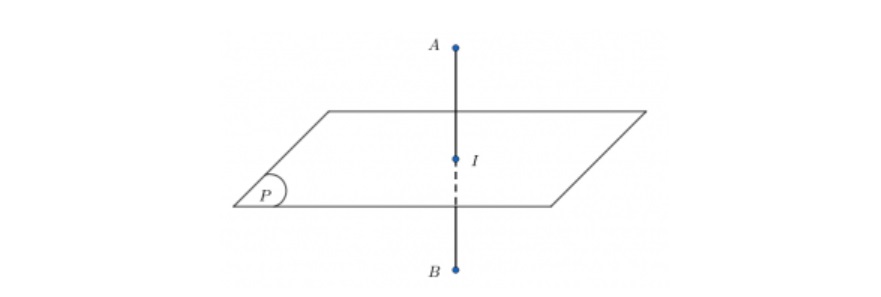
Tính chất phương trình mặt phẳng trung trực

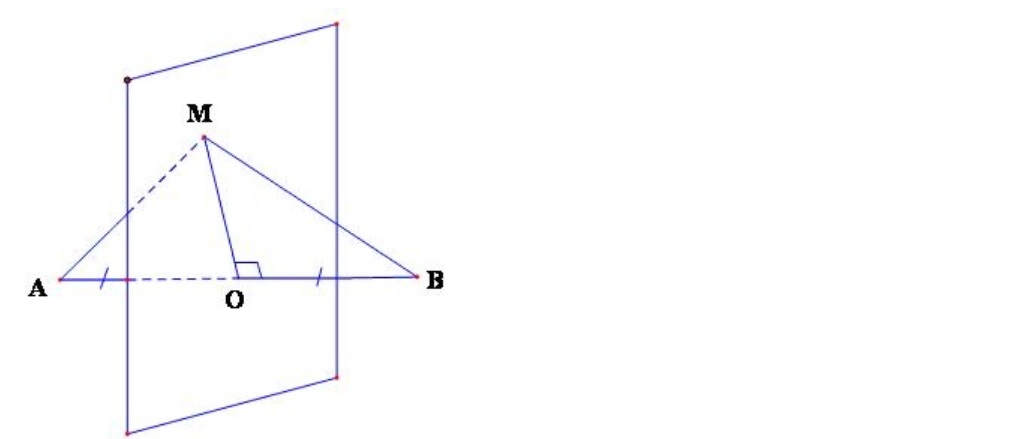
Phương trình mặt phẳng trung trực có tính chất như sau:

• Đi qua điểm trung điểm của đoạn thẳng nối hai điểm bất kỳ trên mặt phẳng
• Pháp tuyến của mặt phẳng là vectơ đơn vị của đoạn thẳng nối hai điểm bất kỳ trên mặt phẳng
• Phương trình của mặt phẳng trung trực có dạng: ax + by + cz +d=0, trong đó (a,b,c) là vectơ pháp tuyến của mặt phẳng và (x,y,z) là tọa độ của điểm nằm trên mặt phẳng.
• Nếu ta chọn hai điểm bất kỳ trên đoạn thẳng AB và tính phương trình mặt phẳng trung trực của chúng, ta sẽ thu được cùng một phương trình mặt phẳng.
• Mặt phẳng trung trực của đoạn thẳng AB chia không gian thành hai nửa không gian đối xứng qua đường thẳng chứa đoạn thẳng AB.

Sơ đồ hóa hệ thống của phương trình mặt phẳng

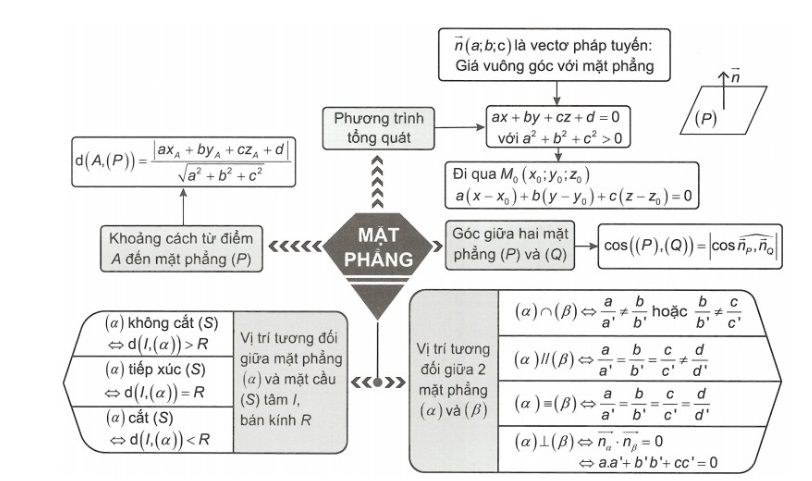
Cách viết phương trình mặt phẳng trung trực đơn giản

Để viết phương trình mặt phẳng trung trực của đoạn thẳng AB, ta cần biết tọa độ của hai điểm A và B. Sau đó, ta tính được điểm trung điểm của đoạn thẳng AB bằng cách lấy trung bình cộng của các tọa độ của A và B.

• Bước 1: Tìm tọa độ trung điểm của mặt phẳng
• Bước 2: Tìm vecto AB là vectơ pháp tuyến của mặt phẳng P
• Bước 3: Viết phương trình mặt phẳng trung trực đi qua điểm I của Vecto AB

Ví dụ: Hãy tạo phương trình cho mặt phẳng trung trực của đoạn thẳng AB, trong đó A có tọa độ (1, -2, 4) và B có tọa độ (3, 6, 2).

Điểm I(2; 2; 3) là trung điểm của đoạn thẳng AB.

Tìm mặt phẳng trung trực của đoạn AB đi qua I,

Với vectơ pháp tuyến được yêu cầu ta có =>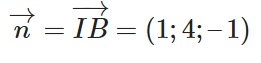

Lúc này phương trình mặt phẳng của đoạn thẳng AB sẽ được viết như sau:

=> 1(x – 2) + 4(y – 2) – 1(z – 3) = 0 hoặc x + 4y – z – 7 = 0

Dạng bài tập về phương trình mặt phẳng trung trực hay dùng

Bài tập 1: Hãy lập phương trình của mặt phẳng trung trực của đoạn AB với A(2; 3; 7), B(4; 1; 3).

Lời giải:

Gọi M là trung điểm của đoạn thẳng AB

Lúc này ta xác định tọa động của M là

=> M = ((2+4)/2; (3+1)/2; (7+3)/2) từ đây ta có thể thất M (3; 2; 5)

Bài tập 2: Trong không gian Oxyz, có hai điểm A(1;2;3) và B(3;2;1). Hãy tìm phương trình mặt phẳng trung trực của đoạn thẳng AB.

Lời giải:

Để viết phương trình mặt phẳng trung trực của đoạn thẳng AB, ta cần tìm tọa độ điểm trung điểm của đoạn thẳng AB.

Tọa độ trung điểm của đoạn thẳng AB là ((1+3)/2, (2+2)/2, (3+1)/2) = (2, 2, 2).

Phương trình mặt phẳng trung trực của đoạn thẳng AB là:

(x - 2) + (y - 2) - (z - 2) = 0 => rút gọn x-z=0

Bài tập 3: Cho tam giác ABC với tọa độ A(1, 2, 3), B(4, 5, 6) và C(7, 8, 9). Viết phương trình mặt phẳng trung trực của đường thẳng AB.

Lời giải:

Ta có:

Tọa độ trung điểm của đường thẳng AB là ((1+4)/2, (2+5)/2, (3+6)/2) = (2.5, 3.5, 4.5)

Vector này sẽ vuông góc với đường thẳng AB và do đó sẽ song song với vector chỉ phương của đường thẳng AB.

=> Vector chỉ phương của đường thẳng AB là (4-1, 5-2, 6-3) = (3, 3, 3)

Phương trình mặt phẳng trung trực của đường thẳng AB là:

-3(x - 2.5) - 3(y - 3.5) + 3(z - 4.5) = 0 ⇔ -x - y + z = 5.5

Bài tập 4: Trong không gian Oxyz, có hai điểm A(1;2;3) và B(3;6;1). Mặt phẳng (P) là mặt phẳng trung trực của đoạn thẳng AB. Hãy viết phương trình tổng quát của mặt phẳng (P).

Lời giải:

Điểm trung điểm của đoạn thẳng AB có tọa độ là:

=> M = ((1+3)/2; (2+6)/2; (3+1)/2) = (2; 4; 2)

Vecto nối hai điểm AB là: AB = B - A = (3-1; 6-2; 1-3) = (2; 4; -2)

Do (P) là mặt phẳng trung trực của đoạn AB, nên điểm M nằm trên mặt phẳng (P). Vậy, một phương trình tổng quát của mặt phẳng (P) có thể được viết dưới dạng:

2(x−2)+4(y−4)−2(z−2)=0 ⇔2x+4y−2z−16=0 ⇔x+2y−z−8=0.

Bài tập 5: Hãy viết phương trình của mặt cầu ngoại tiếp tứ diện ABCD với các điểm A(1;-1;0), B(3;1;2), C(-1;0;2) và D(-1;3;0).

Lời giải

Gọi I,M,N là trung điểm của AB,BC, CD

Ta có:

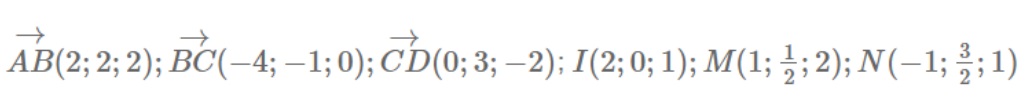
Gọi P,Q,R lần lượt là mặt phẳng trung trực của đoạn AB,BC và CD ta có:

Gọi K là tâm của mặt cầu ngoại tiếp tứ diện và K là giao điểm của mặt phẳng trung trực P ,Q,R. Tọa độ K là nghiệm của phương trình:

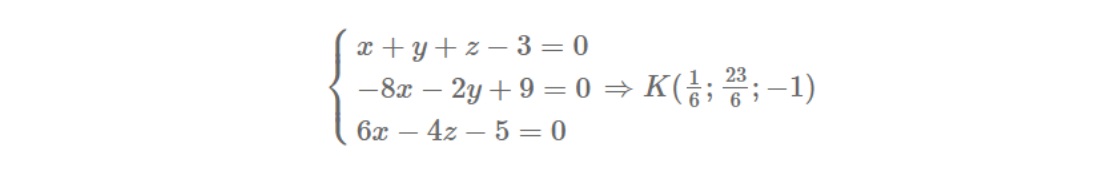
Ta xác định bán kính R của mặt cầu là R=KA

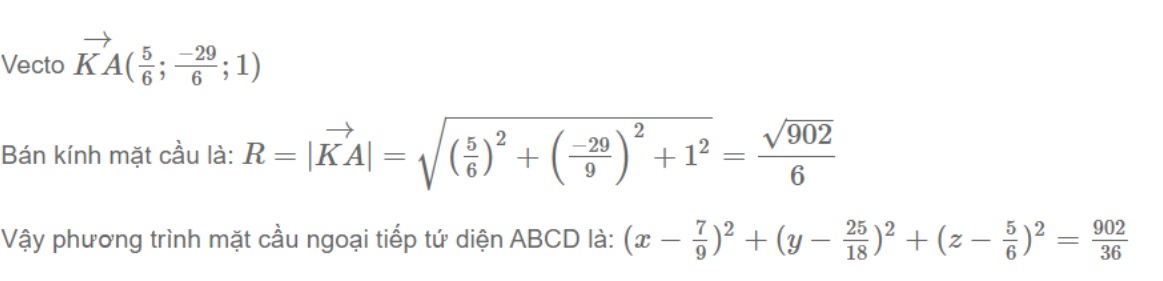
Kết luận

Trên đây là những lý thuyết về phương trình mặt phẳng trung trực mà thầy phú muốn gửi đến các em học sinh. Hy vọng rằng những nội dung này sẽ giúp các bạn dành được điểm cao trong các bài thi sắp tới. Đừng quên truy cập trang web thayphu.net để có thêm nhiều kiến thức hay nhé! Chúc các bạn giành được điểm tuyệt đối!