Cách viết phương trình đường trung tuyến trong tam giác

Phương trình đường trung tuyến trong tam giác có rất nhiều cách viết, nhưng đấu là cách viết chúng ta có thể áp dụng trong mọi bài toán, từ cơ bản đến nâng cao.

Phương trình đường trung tuyến là một nội dung quan trọng trong toán học, nó được ứng dụng khá nhiều trong học tập và cả chương trình nghiên cứu. Nếu bạn vẫn chưa biết viết công thức của phương trình này, hãy đọc bài viết sau đây nhé! Ở đây, Thayphu sẽ giúp bạn phân tích và giải quyết tất cả các bài toán có liên quan đến đường trung tuyến trong tam giác một cách dễ hiểu nhất.

Đinh nghĩa đường trung tuyến của tam giác

Hình ảnh biểu thị 3 đường trung tuyến trong tam giác ABC

Trong một đường thẳng, đường thẳng được gọi là đường trung tuyến khi nó đi qua trung điểm của đường thẳng đó. Còn trong tam giác, đường thẳng nối từ đỉnh này đến trung điểm của cạnh đối diện được gọi là đường trung tuyến. Bất kỳ một tam giác nào cũng sẽ có 3 đường trung tuyến, và chúng giao nhau tại một điểm, gọi là trọng tâm.

Như vậy, khái niệm phương trình đường trung tuyến là phương trình của những đường thẳng nối từ đỉnh đến trung điểm của cạnh đối diện. Thông thưởng, người ta gọi đó là phương trình tổng quát bởi vì với bất kỳ một tam giác nào, chúng ta đều có thể áp dụng nó.

Cách viết phương trình đường trung tuyến AM trong tam giác

Hướng dẫn cách viết phương trình tổng quát đường trung tuyến AM

Cách để viết được phương trình đường trung tuyến trong tam giác cực kỳ đơn giản. Nếu vẫn chưa nắm được các bước tổng quát để viết loại phương trình đường thẳng này, các bạn hãy làm theo 4 bước hướng dẫn sau nhé!

• Bước 1: Đầu tiên, các bạn cần phải xác định được tọa độ của ba đỉnh hình tam giác.
• Bước 2: Tiếp đến, các bạn hãy tìm tọa độ của các trung điểm cạnh tam giác.
• Bước 3: Sử dụng công thức viết phương trình đường thẳng đi qua hai điểm cho trước để viết phương trình đường trung tuyến được yêu cầu.
• Bước 4: Tương tự, bạn áp dụng công thức vừa tìm được để viết phương trình đường trung tuyến cho các cạnh khác của tam giác.

Bài tập vận dụng

Sau đây, Thayphu sẽ giúp các bạn giải quyết một số dạng bài toán viết phương trình đường trung tuyến trong tam giác:

Bài 1: Cho tam giác ABC với tọa độ các đỉnh là: A(1;1), B(0;-2), C(4;2). Viết các phương trình trung tuyến của tam giác ABC này.

Lời giải chi tiết:

• Bước 1: Xác định được tọa độ của ba đỉnh hình tam giác ABC, cụ thể đề bài đã cho: A(1;1), B(0;-2), C(4;2)
• Bước 2: Tìm tọa độ của các trung điểm cạnh tam giác AB, AC, BC.

Nhắc lại lý thuyết: Tìm tọa độ trung điểm M của đoạn thẳng AB.

• xM = (xA + xB)/2
• yM = (yA + yB)/2

Áp dụng công thức trên, ta xác định tọa độ của ba trung điểm cạnh AB, AC, BC như sau:

E(0.5;-0.5), D(2.5;1.5), F(2;0)

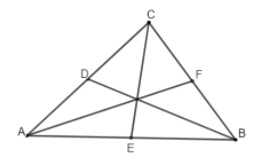
• Bước 3: Viết phương trình đường trung tuyến AF, BD, CE.

Đường trung tuyến AF: phương trình đường thẳng đi qua điểm A(1;1) và điểm trung điểm của cạnh BC là F(2;0)

y-1= [(0-1)/(2-1)](x-1)

⇔ y-1 = -(x-1)

⇔ dAF: y = -x+2

Đường trung tuyến BD: phương trình đường thẳng đi qua điểm B(0;-2) và điểm trung điểm của cạnh AC là D(2.5;1.5)

y+2 = [(1.5+2)/(2.5-0)](x-0)

⇔ y+2 = 1.4x

⇔ dBD: y = 1.4x-2

Đường trung tuyến CE: phương trình đường thẳng đi qua điểm C(4;2) và điểm trung điểm của cạnh AB là E(0.5;-0.5).

y-2 = [(-0.5-2)/(0.5-4)](x-4)

⇔ y-2 = (5/7)(x-4)

⇔ dCE: y = (5x-6)/7

• Bài 2: Cho tam giác ABC với tọa độ các đỉnh là: A(1;2), B(3;0), C(-1;2). Viết các phương trình chỉ phương của ba đường trung tuyến trong tam giác ABC này.

Lời giải:

Gọi I, M, N là trung điểm của BC, AC, AB, khi đó tọa độ của 3 điểm này lần lượt là: I(1;1), M(0;2), N(2;1).

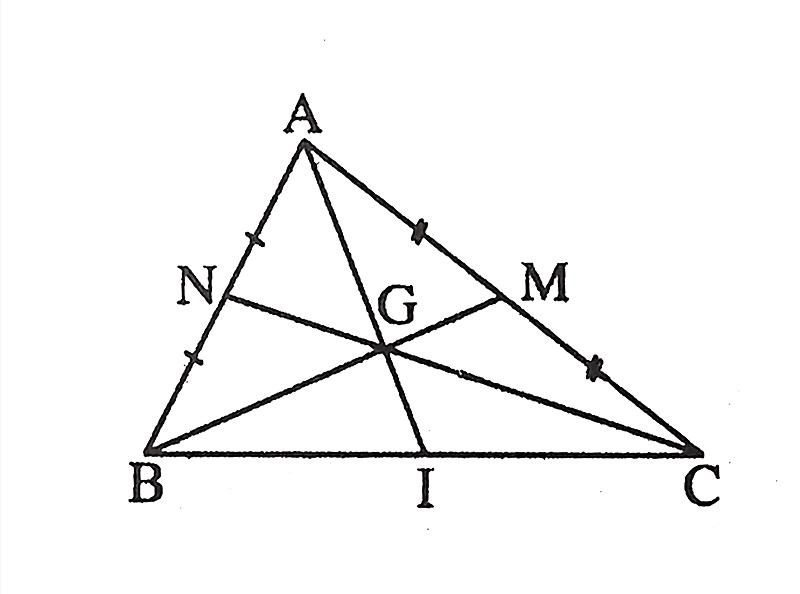
Phương trình chỉ phương của ba đường trung tuyến AI, BM, CN trong tam giác ABC là:

Đường trung tuyến AI nhận vecto AI(0;-1) là vecto chỉ phương => Phương trình chỉ phương của đường trung tuyến AI là:

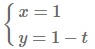
Đường trung tuyến BM nhận vecto BM(-3;2) là vecto chỉ phương => Phương trình chỉ phương của đường trung tuyến BM là:

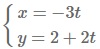
Đường trung tuyến CN nhận vecto CN(3;-1) là vecto chỉ phương => Phương trình chỉ phương của đường trung tuyến CN là:

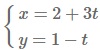
• Bài 3: Cho tam giác ABC, trong đó đỉnh B có tọa độ (-3;0), AH là đường cao với dAH: 2x - y=0 và AM là đường trung tuyến với dAM: x -1=0. Biết dAH: 2x-y=0, dAM: x-1=0.Hãy viết phương trình đường trung tuyến CN của tam giác ABC.

Lời giải:

A giao điểm của hai đường thẳng AH và AM nên tọa độ của điểm A là nghiệm của hai dAH và dAM => A(1;2)

N là trung điểm đoạn AB => N(2;1)

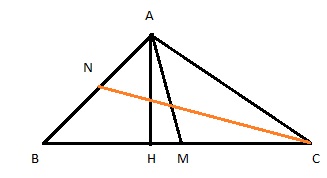
Do BC và AH vuông góc với nhau, dBC có dạng x+2y+c=0.

Vì B(3;0) nằm trên dBC, thay x=3, y=0 => c=-3

M giao điểm của hai đường thẳng BC và AM nên tọa độ của điểm M là nghiệm của hai dBC và dAM => M(1;1)

M(1;1) là trung điểm của B(-3;0) và C => C(-1;2)

Viết phương trình trung tuyến CN với C(-1;2) và N(2;1):

Vecto CN(-3;1) => Vecto pháp tuyến của CN là (1;3)

dCN: 1(x-2) + 3(y-1) = 0

dCN: x + 3y = 4

Vậy phương trình đường trung tuyến CN của tam giác ABC là x + 3y = 4.

Như vậy, dựa vào những nội dung Thayphu đã cung cấp, cùng với những bài toán mẫu trên đây, chắc hẳn bạn đã phần nào hiểu được khái niệm cũng như cách phương trình đường trung tuyến. Hy vọng rằng, sau khi tham khảo bài viết này các bạn sẽ không còn cảm thấy khó khăn khi làm những bài toán liên quan đến phương trình của đường trung tuyến nữa. Chúc bạn học tốt!