Mét khối là gì? Chuyển đối M3 đầy đủ và bài tập áp dụng

Mét khối được kí hiệu là m3 là một hình khối đặc biệt trong hình hộp chữ nhật. Hãy cùng chúng tôi tìm hiểu về m3 cũng như bài tập áp dụng nhé.

M3 là một trong những hình đơn giản và phổ biến nhất trong hình học không gian. Nó có ứng dụng trong nhiều lĩnh vực như kiến trúc, xây dựng, thiết kế và nhiều ứng dụng khác. Trong bài viết này của thayphu chúng ta sẽ tìm hiểu sâu hơn về định nghĩa và các tính chất của m3.

Định nghĩa về mét khối

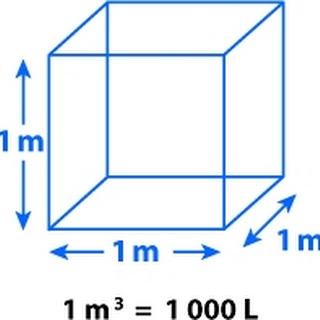
Định nghĩa về mét khối

M3 là một hình có sáu mặt hình chữ nhật đồng dạng và vuông góc với nhau. Chúng có ba cặp cạnh song song với nhau và tất cả các góc là góc vuông (90 độ). Để tính m3 ta chỉ cần lấy độ dài mỗi cạnh nhân lại với nhau

Ví dụ: Một hình có chiều dài 5m chiều rộng 6m chiều cao 7m hãy tính thể tích của hình đó

Đáp án: V = 5 ×6 ×7 = 210m3

Ứng dụng của m3

Mét khối không chỉ có trong toán học mà còn được ứng rộng rãi trong thực tế như kiến trúc và xây dựng.

Trong kiến trúc

Trong kiến trúc bạn có thể sử dụng m3 để xây dựng nhà ở hoặc toà nhà cao tầng và nhiều công trình kiến trúc hiện đại khác..

Trong công nghiệp

Trong công nghiệp m3 có vai trò là đóng gói sản phẩm, thiết kế sản phẩm, hoặc vận chuyển các sản phẩm…

Tổng hợp công thức tính m3

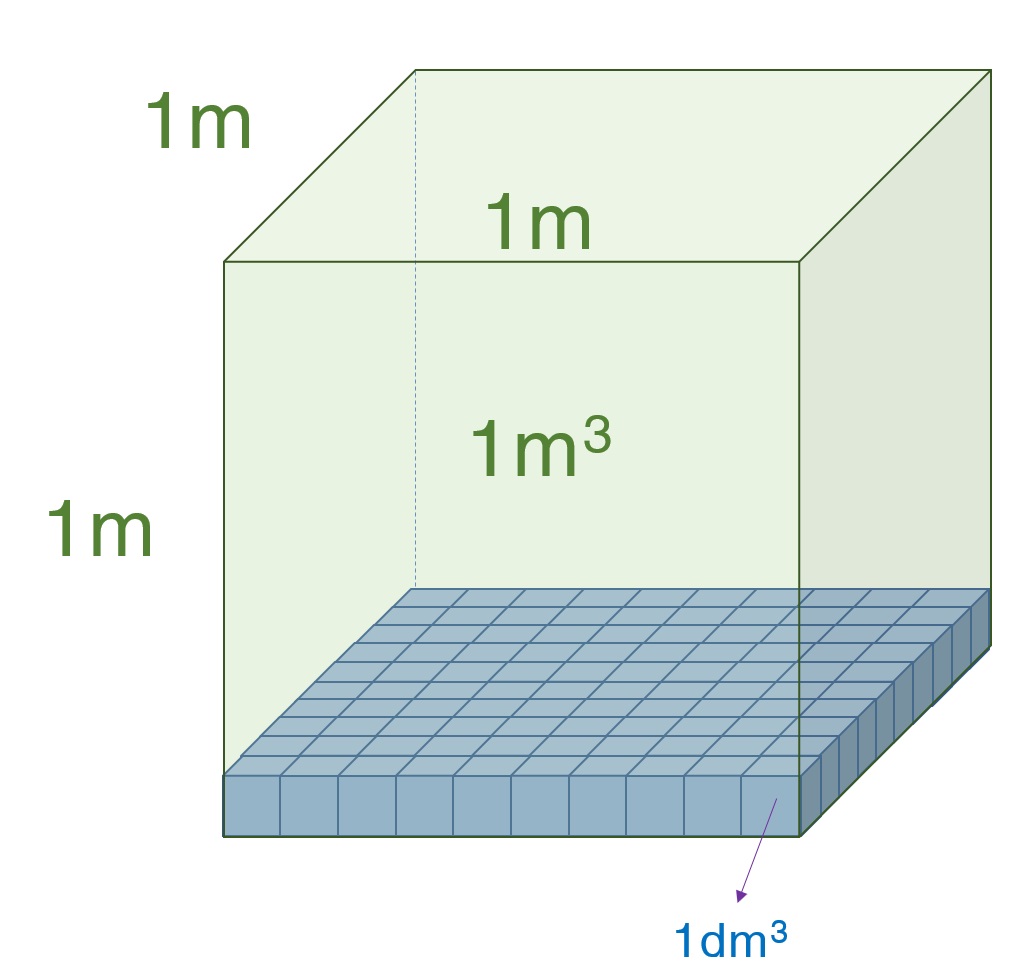
Tổng hợp công thức tính m3

Khi làm việc với m3 thì ta cần phải biết công thức để giải các bài toán liên quan đến mét khối. Dưới đây chúng tôi đã tổng hợp những công thức tính m3:

Cách tính diện tích bề mặt m3

Diện tích bề mặt của mét khối được hiểu là tổng diện tích của sáu mặt hình chữ nhật tạo nên hình khối đó.

Công thức để tính diện tích bề mặt (S) là:

S = 2(ab + bc + ac)

Trong đó:

• a là chiều dài
• b là chiều rộng
• c là chiều cao

Ví dụ: Giả sử chúng ta có một m3 với các kích thước:

• Chiều dài (a) = 5 m
• Chiều rộng (b) = 3 m
• Chiều cao (c) = 4 m

Áp dụng công thức, ta có:

S = 2(ab + bc + ac) S = 2[(5 × 3) + (3 × 4) + (5 × 4)] S = 2(15 + 12 + 20) S = 2 × 47 S = 94 m²

Cách tính diện tích mỗi mặt của mét khối

Để tính diện tích của mỗi mặt trong m3, ta sử dụng công thức sau:

Diện tích mỗi mặt = chiều dài × chiều rộng

Với m3 có kích thước a, b, c, ta có:

• Diện tích mặt trên và mặt dưới: ab
• Diện tích mặt trước và mặt sau: bc
• Diện tích mặt bên trái và mặt bên phải: ac

Công thức tính thể tích mét khối

Thể tích là một khái niệm quan trọng trong hình học không gian, đặc biệt là khi làm việc với mét khối.

Công thức tính thể tích (V) của m3 là:

V = a × b × c

Trong đó:

• a là chiều dài
• b là chiều rộng
• c là chiều cao

Ví dụ: Giả sử chúng ta có một m3 có chiều dài 8m chiều rộng 5m chiều cao 3m. Hãy tính thể tích

Áp dụng công thức, ta có:

• V = a × b × c
• V = 8 m × 5 m × 3 m
• V = 120 m³

Bài toán liên quan đến mét khối

Khi làm việc với m3 chúng ta cần phải biết liên quan đến chúng dưới đây chúng tôi đã tổng hợp những bài toán liên quan đến m3

Dạng 1: Tính thể tích hình khối

Công thức: Thể tích (m³) = Chiều dài (m) x Chiều rộng (m) x Chiều cao (m)

Ví dụ: Tính thể tích của một hộp có kích thước 5m x 3m x 2m.

Giải: Thể tích = 5m x 3m x 2m = 30m³

Dạng 2: Tính khối lượng của một vật

Công thức: Khối lượng (tấn) = Thể tích (m³) x Khối lượng riêng (tấn/m³)

Ví dụ: Tính khối lượng của 500m³ cát biết rằng khối lượng riêng của cát là 1,6 tấn/m³.

Giải: Khối lượng = 500m³ x 1,6 tấn/m³ = 800 tấn

Dạng 3: Tính thể tích bể chứa

Công thức: Thể tích (m³) = Chiều dài (m) x Chiều rộng (m) x Chiều cao (m)

Ví dụ: Tính thể tích của một bể chứa có kích thước 8m x 5m x 3m.

Giải: Thể tích = 8m x 5m x 3m = 120m³

Dạng 4: Tính khối lượng nước cần đổ vào bể

Công thức: Khối lượng nước (tấn) = Thể tích bể (m³) x Khối lượng riêng nước (tấn/m³)

Ví dụ: Tính khối lượng nước cần đổ vào một bể có thể tích 150m³.

Giải: Khối lượng nước = 150m³ x 1 tấn/m³ = 150 tấn

Dạng 5: Tính diện tích bề mặt của hình khối

Công thức: Diện tích bề mặt (m²) = 2 x (Chiều dài x Chiều rộng + Chiều dài x Chiều cao + Chiều rộng x Chiều cao)

Ví dụ: Tính diện tích bề mặt của một hộp có kích thước 4m x 3m x 2m.

Giải: Diện tích bề mặt = 2 x (4m x 3m + 4m x 2m + 3m x 2m) = 52m²

Dạng 6: Tính thể tích của một đường ống

Công thức: Thể tích (m³) = π x (Đường kính (m))² x Chiều dài (m) / 4

Ví dụ: Tính thể tích của một đường ống có đường kính 0,5m và chiều dài 20m.

Giải: Thể tích = π x (0,5m)² x 20m / 4 = 3,927m³

Dạng 7: Tính khối lượng một vật liệu

Công thức: Khối lượng (tấn) = Thể tích tràn (m³) x Khối lượng riêng (tấn/m³)

Ví dụ: Tính khối lượng của một lượng sỏi tràn khỏi một xe tải có thể tích 12m³, biết rằng khối lượng riêng của sỏi là 1,8 tấn/m³.

Giải: Khối lượng = 12m³ x 1,8 tấn/m³ = 21,6 tấn

Dạng 8: Tính lượng nhiên liệu cần thiết

Công thức: Lượng nhiên liệu (lít) = Thể tích (m³) x Mật độ nhiên liệu (lít/m³)

Ví dụ: Tính lượng nhiên liệu cần thiết để lấp đầy một bể có thể tích 8m³, biết rằng mật độ của nhiên liệu là 850 lít/m³.

Giải: Lượng nhiên liệu = 8m³ x 850 lít/m³ = 6.800 lít

Bài tập áp dụng

Câu 1: Thể tích của một hình hộp chữ nhật có kích thước 4m x 3m x 2m là:

A. 16 m³

B. 24 m³

C. 32 m³

D. 48 m³

Đáp án: C. 32 m³

Câu 2: Bể chứa nước có kích thước 6m x 4m x 3m. Thể tích của bể chứa nước này là:

A. 48 m³

B. 72 m³

C. 84 m³

D. 96 m³

Đáp án: B. 72 m³

Câu 3: Một đường ống có đường kính 0,5m và chiều dài 10m. Thể tích của đường ống này là:

A. 1,96 m³

B. 3,92 m³

C. 7,85 m³

D. 15,71 m³

Đáp án: B. 3,92 m³

Câu 4: Một hộp có kích thước 5m x 4m x 3m. Diện tích bề mặt của hộp này là:

A. 60 m²

B. 80 m²

C. 100 m²

D. 120 m²

Đáp án: D. 120 m²

Câu 5: Một xe tải chứa 15 m³ cát. Biết rằng khối lượng riêng của cát là 1,8 tấn/m³. Khối lượng của cát trên xe tải là:

A. 15 tấn

B. 22,5 tấn

C. 27 tấn

D. 30 tấn

Đáp án: C. 27 tấn

Câu 6: Thể tích của một tấm gỗ có kích thước 4m x 1,5m x 0,2m là:

A. 1,2 m³

B. 1,4 m³

C. 1,6 m³

D. 1,8 m³

Đáp án: A. 1,2 m³

Câu 7: Một đường ống có đường kính 0,4m và chiều dài 15m. Thể tích của đường ống này là:

A. 3,14 m³

B. 4,71 m³

C. 6,28 m³

D. 7,85 m³

Đáp án: B. 4,71 m³

Câu 8: Một bể chứa có kích thước 6m x 4m x 3m. Khối lượng nước cần để lấp đầy bể này là:

A. 72 tấn

B. 90 tấn

C. 108 tấn

D. 120 tấn

Đáp án: A. 72 tấn

Câu 9: Một hộp có kích thước 3m x 2m x 1,5m. Diện tích bề mặt của hộp này là:

A. 27 m²

B. 30 m²

C. 33 m²

D. 36 m²

Đáp án: C. 33 m²

Câu 10: Một xe tải chứa 20 m³ đá sỏi. Biết rằng khối lượng riêng của đá sỏi là 1,6 tấn/m³. Khối lượng của đá sỏi trên xe tải là:

A. 20 tấn

B. 24 tấn

C. 32 tấn

D. 40 tấn

Đáp án: C. 32 tấn

Trên đây là một số thông tin cơ bản về m3 từ định nghĩa, tính chất, cách tính diện tích bề mặt và thể tích, đến ứng dụng trong thực tế thayphu.net hi vọng bạn nắm vững kiến thức này và các bài tập để không bị sai sót trong quá trình tính toán.