Cách xác định mặt phẳng đối xứng của khối đa diện và bài tập

Mặt phẳng đối xứng của khối đa diện gồm những khối có nhiều mặt khác nhau thông qua các mặt phẳng. Đây là một kiến thức khá là quan trọng trong toán học.

Khái niệm về mặt phẳng đối xứng là rất quan trọng trong toán học và được áp dụng rộng rãi trong thực tế. Các khối đa diện như khối lập phương, khối hộp chữ nhật thường có những mặt phẳng đối nhau. Trong bài viết này, thayphu sẽ giới thiệu đến các em học sinh về mặt phẳng này.

Định nghĩa về mặt phẳng đối xứng

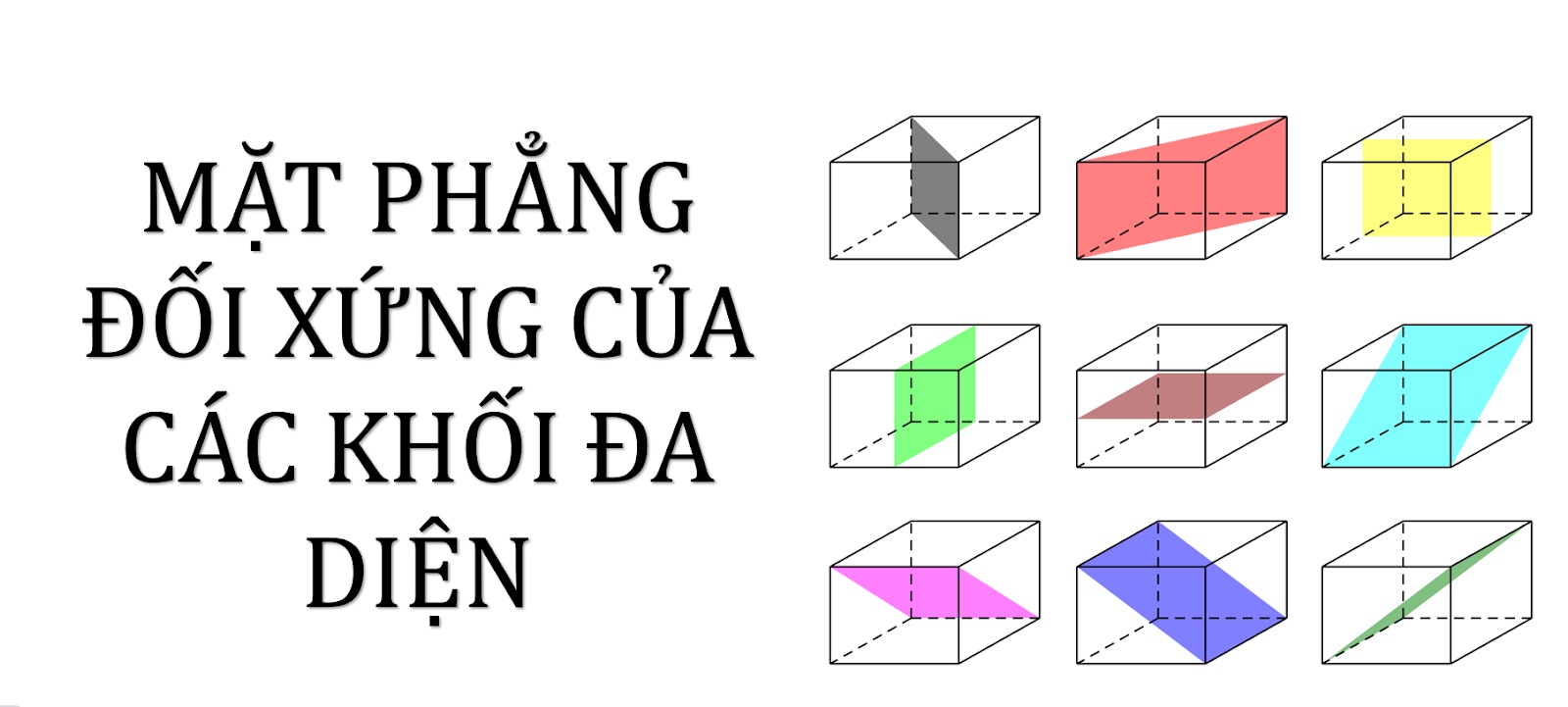
Các khối đa diện sẽ được xác định mặt phẳng khác nhau

Quy luật: do tính chất đối xứng nhau nên cứ đi từ trung điểm các cạch ra mà tìm. Đảm bảo rằng nếu chọn 1 mặt phẳng đối xứng nào thì các điểm còn dư phải chia đều về 2 vế.

Mặt phẳng đối xứng được định nghĩa thông qua ví dụ sau:

Khối đa diện được ký hiệu là H và khi thực hiện phép đối xứng qua mặt phẳng P, H sẽ giữ nguyên. Trong trường hợp này, P được gọi là mặt đối xứng của khối đa diện H.

Cách xác định mặt phẳng đối xứng của các khối đa diện

Để giúp bạn nhận biết được các mặt phẳng đối xứng của các khối đa diện phổ biến, dưới đây là danh sách một số mặt phẳng.

Mặt phẳng đối xứng của tứ diện đều

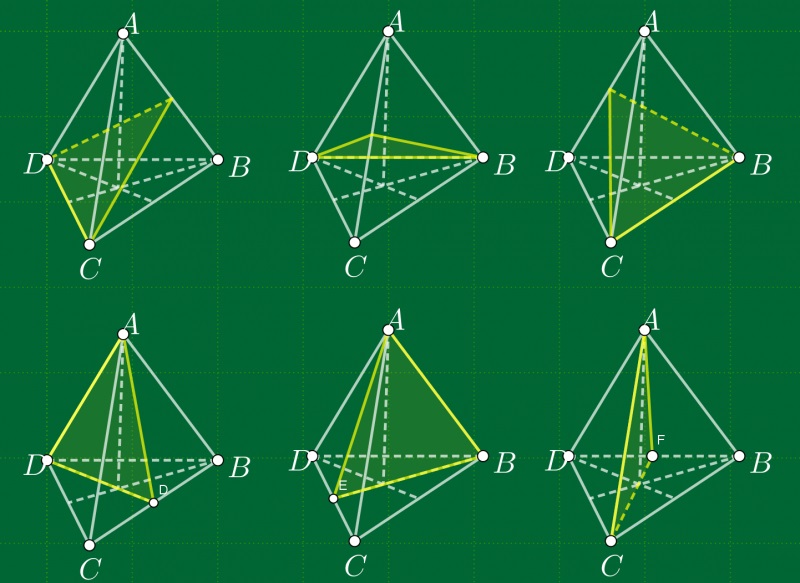
Mặt phẳng đối xứng của tứ diện đều

Ta có thể xác định được sẽ có 6 mặt phẳng của tứ diện đều và được xác định là khi một phặt phẳng chứa một cạnh của tứ diện mà đi qua trung điểm của cạnh đối diện thì chính là mặt phẳng . Từ hình vẽ ta có thể nhìn thấy rõ ràng được đâu là mặt phẳng đối xứng của tứ diện.

Mặt phẳng đối xứng của lăng trụ tam giác đều

Trước tiên ta phải hiểu được lăng trụ tam giác đều là gì? lăng trụ tam giác đều là các trụ đứng và có 2 mặt đáy là hai tam giác đều.

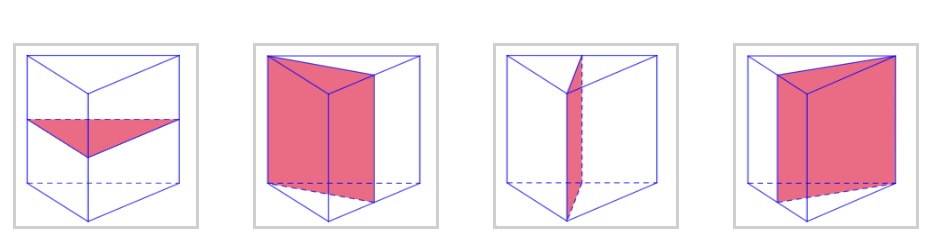
Trong lăng trụ tam giác đều sẽ có 4 mặt phẳng đối xứng và được xác định:

• Lăng trụ sẽ có 3 mặt phẳng mỗi mặt phẳng sẽ chưa một cạnh của tam giác đều và đi qua trung điểm của các cạnh đối diện tạo hình một mặt phẳng hình chữ nhật.

• Một mặt phẳng sẽ đi qua trung điểm của tất cả các cạnh bên tạo một mặt phẳng đối xứng hình tam giác.

Mặt phẳng đối xứng của hình chóp tứ giác đều

Hình chóp tứ giác đều là hình có đáy là một tứ giác đều và có 4 cạnh bên có một chiều dài bằng nhau.

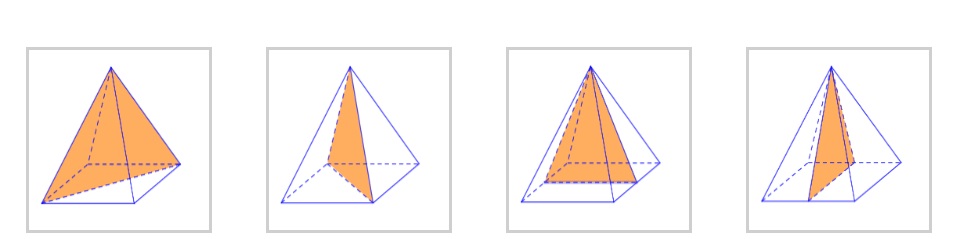
Để xác định ta thấy được đỉnh sẽ được chiếu vuông góc với tâm của hình tứ giác đều đáy. Lúc này ta tiếp tục xác định được hình chiếu tam giác đều:

Hai mặt phẳng sẽ chứa đỉnh và một mặt phẳng đi qua 2 đường chéo khác nhau. Và 2 mặt phẳng đi qua trung điểm của các cạnh đối diện được gọi là mặt phẳng đối xứng của hình chóp tứ giác.

Mặt phẳng đối xứng của hình lập phương

Hình lập phương có 6 mặt phẳng với 6 hình vuông của các cạnh bằng nhau. Trong hình lập phương sẽ được xác định 9 mặt phẳng đối xứng. Như vậy ta có thể xác định như sau:

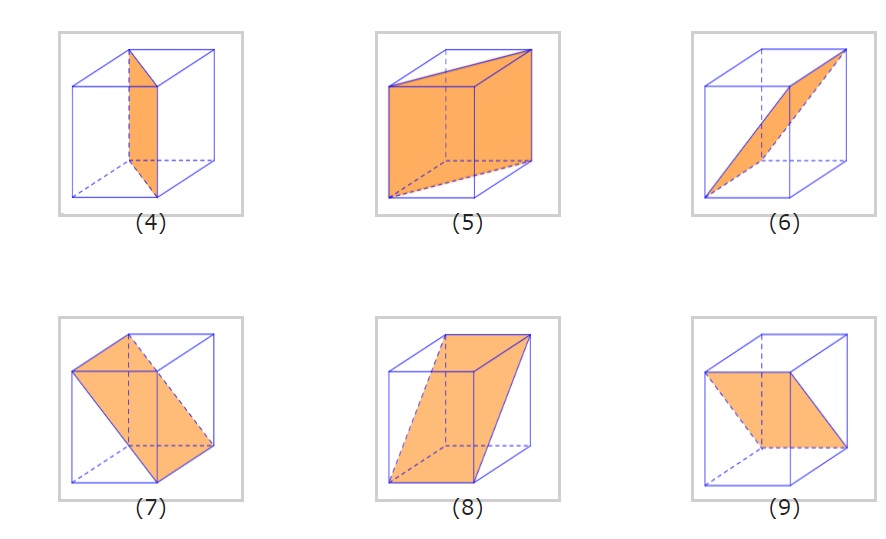
Có 3 mặt phẳng chia hình lập phương thành hai hình hộp chữ nhật bằng nhau. Nới cách dễ hiểu hơn là 3 mặt phẳng sẽ lần lượt chứa các trung điểm của cạnh song song.

Có 6 mặt phẳng sẽ chia hình lập phương thành 2 hình lăng trụ bằng nhau. Có nghĩa là các mặt sẽ đi qua một đường chéo đáy của hai cạnh bên tạo thành 4 điểm đối xứng nhau.

Mặt phẳng đối xứng của hình hộp chữ nhật ( không phải là hình lập phương)

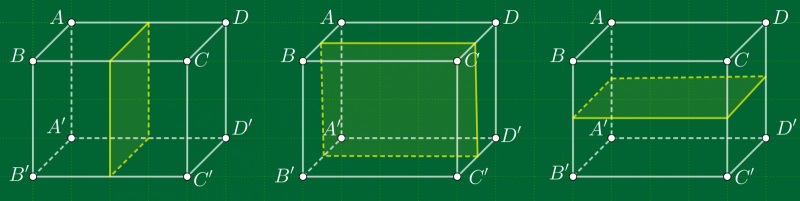
Mặt phẳng đối xứng được xác định khi 3 mặt phẳng đi qua trung điểm của 4 cạnh song song.

Mặt phẳng đối xứng của các hình bát diện đều

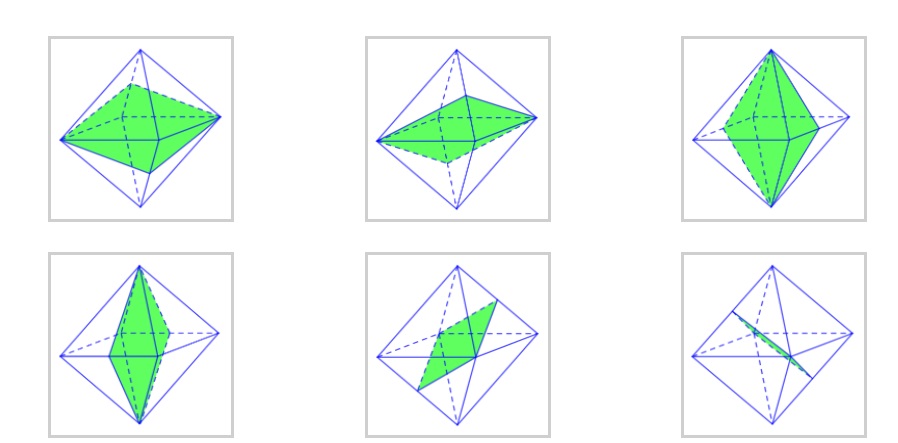
Sẽ có 9 mặt phẳng đối xứng của hình bát diện đều trong đó:

• Có 3 mặt phẳng chia bát diện đều thành 2 khối chóp với tất cả các cạnh đều bằng nhau.

• Có 6 mặt phẳng có điểm đi qua cặp đỉnh đối diện và có 2 mặt cho mỗi cặp định.

Một số dạng bài tập về mặt phẳng đối xứng

Bài 1: Chỉ ra mặt phẳng đối xứng của tứ diện đều ABCD

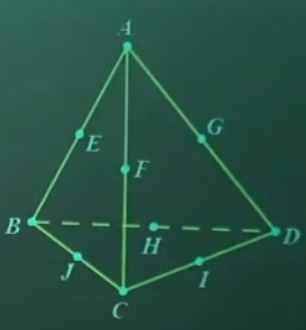
Lời giải

Các mặt phẳng đối xứng của hình tứ diện đều sẽ là: các mặt phẳng chứa một cạnh và đi qua trung điểm cạnh đối diện.

=> ADJ, ABI, ACH, BCG, CDE, BFD,

Bài 2: Chỉ ra mặt phẳng đối xứng của hình chóp tam giác đều sau:

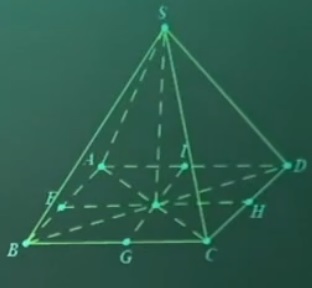
Lời giải

Ở hình chóp tứ giác đều sẽ có 4 mặt phẳng đối xứng đó là:

• Hai mặt phẳng đi qua đỉnh chóp chứa đường trung bình của đáy

• Hai mặt phẳng đi qua đỉnh chóp chứa đường chéo của đáy

=> Mặt phẳng đối xứng của hình chóp trên là: SAC, SBD, SFH, SIG

Bài 3: Hình đa diện nào dưới đây không có tâm đối xứng

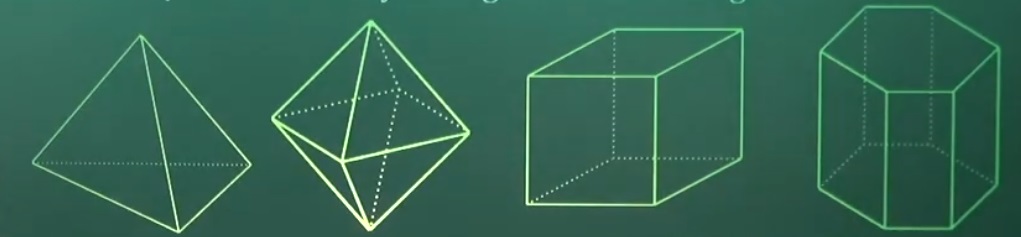
Lời giải

Hình đa diện không có tâm đối xứng là hình Tứ diện đều

Bài 4: Gọi lần lượt là số trục đối xứng của tứ diện đều, khối tứ giác đều, khối lập phương. Hãy chỉ ra số chục đối xứng của các khối đa diện này.

Lời giải

Khối tứ diện đều có 3 trục đối xứng đi qua trung điểm của các cặp cạnh đối diện. Khối hình chóp đều thì có một trục đối xứng đi qua đỉnh và tâm của mặt tứ giác. Và khối lập phương có 9 trục đối xứng đi qua tâm mặt đối diện, đi qua trung điểm của cặp cạnh đối diện.

=> trực đối xứng của tứ diện đều, khối tứ giác đuêỳ, khối lập phương lần lượt là: 3,1,9

Bài 5: Cho hình lập phương ABCD. A’B’C’D’ tâm O đối xứng. Ảnh của mặt phẳng A’B đi qua đối xứng tâm Do là đoạn thẳng nào?

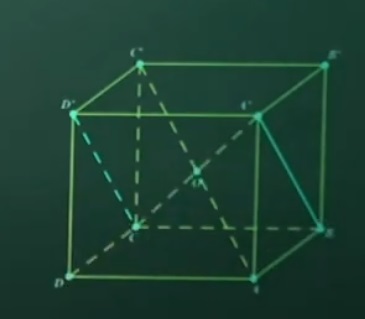
Lời giải

Từ hình vẽ ta có : Do(A’) = C; Do(B)= D’

=> Do(A’B)= CD’

Kết luận

Tóm lại đây là một kiến thức rất đơn giản và dễ xác định chỉ cần các em chú ý và nắm vững kiến thức là có thể ăn điểm ở dạng kiến thức này. Hy vọng rằng bài viết mà thayphu cung cấp sẽ giúp các em biết cách xác định được các mặt phẳng đối xứng của khối đa diện. Chúc các em thành công và dành được điểm cao trong học tập!