Cách tính bán kính và diện tích mặt cầu ngoại tiếp hình chóp

Mặt cầu ngoại tiếp hình chóp dạng toán kết hợp giữa các khối đa diện và khối cầu, công thức tính nhanh m ặt cầu ngoại tiếp hình chóp toán 12.

Mặt cầu ngoại tiếp hình chóp là một dạng toán kết hợp giữa các hình khối đa diện và hình khối cầu. Nó vô cùng quan trọng đối với các em học sinh bởi được xuất hiện hầu hết các bài thi tốt nghiệp quốc gia. Vậy nên hôm nay thayphu sẽ hướng dẫn các em hiểu hơn về dạng toán này qua bài viết dưới đây.

Lý thuyết chung về mặt cầu ngoại tiếp hình chóp

Kiến thức trọng tâm cần ghi nhớ

Mặt cầu là một mặt cầu đi qua hình cầu và đi qua tất cả các đỉnh của khối đa diện đó. Ngay từ khi đầu tiên vào bài điều mà thường hay được hỏi nhất đó là:

• Bán kính R
• Tính diện tích mặt cầu: S= 4пR^2
• Tính thể tích của khối cầu : V= 4/3пR^3

Từ đây ta có quy trình để tính ra mặt cầu ngoại tiếp:

• Xác định được khâu dựng hình và xác định được tâm, bán kính mặt cầu
• Chứng minh cách dựng hình là đúng
• Và tính toán

Công thức tính về mặt cầu ngoại tiếp hình chóp

Ta có thể áp dụng công thức tính như sau:

Khối hình chóp có cạnh bên vuông góc với đáy

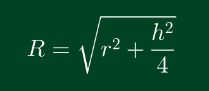
ta có R: Bán kính khối hình chóp ngoại tiếp

h : chiếu cao của khối hình chóp ( là cạnh bên)

r: bán kính đường tròn ngoại tiếp

Khối đa diện có các đỉnh cùng nhìn đoạn AB dưới một góc 90 độ

Hình chóp đều có cạnh bên là SA và chiều cao SO

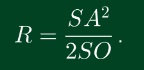
Hình chóp đều có cạnh bên là SAB

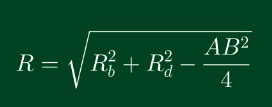
Cách dạng tính bán kính, diện tích mặt cầu ngoại tiếp hình chóp

Sẽ có những dạng mặt cầu thường gặp trong toán học như sau:

Khi đáy là một hình tứ giác ( hình vuông, hình chữ nhật)

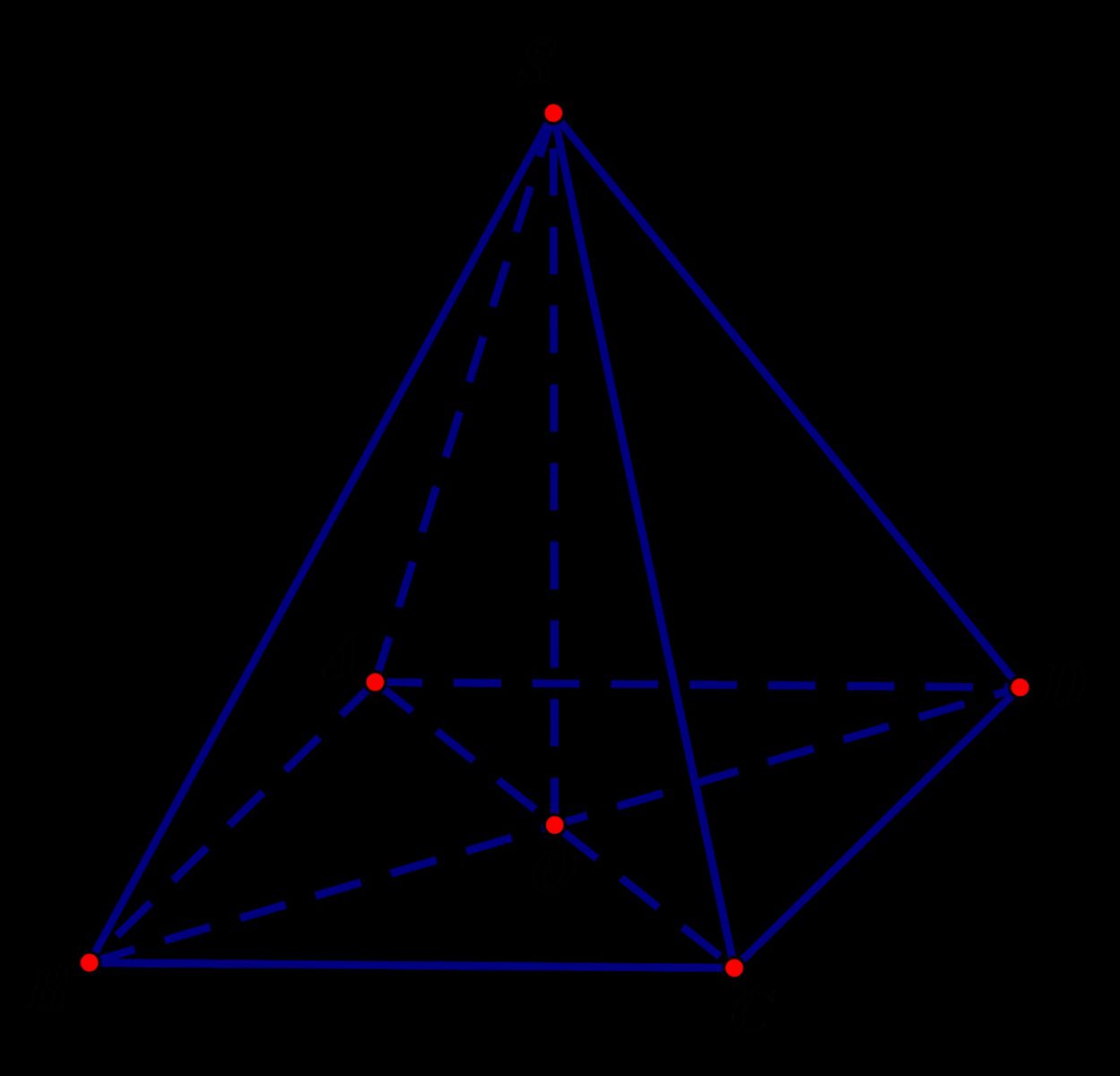
Trước tiên ta phải xác định ra tâm O là điểm giao nhau giữa 2 đường chéo AC và BD. Lúc này OA sẽ được xác định là r.

hình chóp là một tam giác vuông

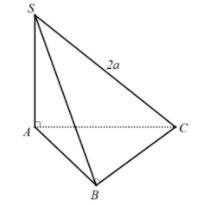
Trung điểm của cạnh huyền từ tâm nối ra đỉnh thì sẽ được xác định là bán kính đáy.

lúc này R=AB/2

Hình chóp đều

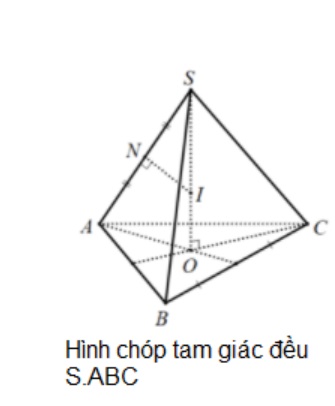
Nếu đáy là một hình tam giác đều thì r sẽ được xác định ⅔ của đường cao vuông góc.

Công thức : R = SA^2/2SO

Hình chóp có các cạnh bên vuông góc với mặt phẳng đáy

Hình chóp S.A1A2...An có cạnh bên SA vuông góc với đáy A1A2...An, đáy được nội tiếp trong đường tròn tâm O. Tâm và bán kính mặt cầu ngoại tiếp hình chóp S.A1A2...An được xác định như sau.

Chúng ta có thể vẽ một đường thẳng vuông góc với đường tròn đáy tại tâm O.

Sau đó, trong mặt phẳng chứa đường thẳng này và các điểm A1, A2, ..., An, ta có thể xây dựng đường trung trực của cạnh SA.

Đường trung trực này sẽ cắt cạnh SA tại điểm N và đường thẳng vuông góc với đường tròn đáy tại điểm I trên đường thẳng đã vẽ trước đó.

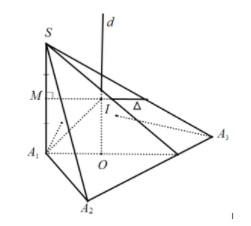
Hình chóp có mặt bên vuông góc với mặt phẳng đáy

Cho hình chóp có mặt bên là tam giác đều SAB, cân tại đỉnh S, vuông tại đỉnh S và nằm trong mặt phẳng vuông góc với đáy. Đặt R là bán kính đường tròn ngoại tiếp tam giác SAB và R d là bán kính đường tròn ngoại tiếp đáy. Bán kính khối cầu ngoại tiếp hình chóp đó: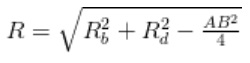

Những dạng bài tập về mặt cầu ngoại tiếp hình chóp thường gặp nhất

Ví dụ 1: Hình chóp S.ABC có đáy ABC là tam giác vuông tại B, SA vuông góc với mặt phẳng (ABC) và SC = 2a. Hãy tính bán kính mặt cầu ngoại tiếp hình S.ABC.

Lời giải

Ta có hình vẽ như sau:

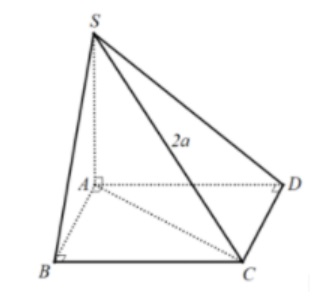
Chứng minh

Ta có:

BC ⊥ BA

BC ⊥ SA

=> BC ⊥ SBA => BC⊥SB

Tương tự

CD ⊥ SD

SA ⊥ (ABCD) ⇒ SA ⊥ AC

Ba điểm A, B, D cùng nhìn SC dưới một góc vuông => bán kính mặt cầu là R = SC/2 = 2a/2 = a

Ví dụ 2: Hình chóp S.ABC có đáy là tam giác cân tại A, AB = a và góc BAC = 120 độ. Cạnh SA vuông góc với đáy và độ dài là 2a. Hãy tính bán kính của mặt cầu ngoại tiếp hình chóp S.ABC.

Lời giải

Ta có hình vẽ sau :

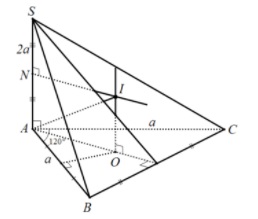
Chứng minh

O là tâm đường tròn ngoại tiếp tam giác ABC

Bắt đầu bằng việc dựng trục d của đường tròn ngoại tiếp tam giác ABC.

Sau đó, trong mặt phẳng (SA,d), vẽ trung trực cạnh SA và cắt d tại I.

Từ đó, có thể suy ra rằng I là tâm mặt cầu ngoại tiếp hình chóp S.ABC và bán kính của mặt cầu là R, với R bằng độ dài của IA, IB, IC và IS.

Ví dụ 3: Cho hình chóp SABC có tam giác ABC vuông tại B , SA vuông góc với mặt

phẳng (ABC) và SC=2a . Tính diện tích và thể tích mặt cầu ngoại tiếp hình chóp trên

Lời giải

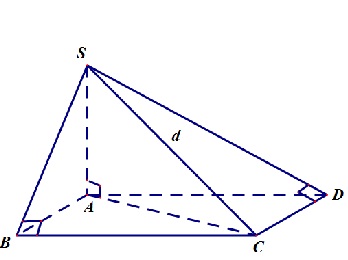
Ta có thể thấy tam giác SAC vuông tại A , tam giác SBC vuông tại B

từ đó ta có công thức: R=SC/2 = 2a/2

Ví dụ 4: Hình chóp S.ABC có đáy là tam giác đều cạnh bằng 1 và mặt bên SAB là tam giác đều nằm trong mặt phẳng vuông góc với mặt phẳng đáy. Hãy tính thể tích V của khối cầu ngoại tiếp hình chóp này.

Lời giải

Ta có hình vẽ

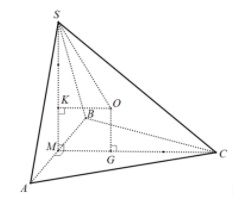
Chứng minh và tính toán

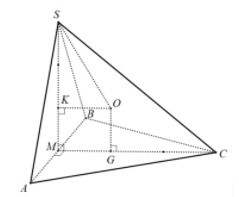
Ví dụ 5: Hình chóp S.ABCD có chiều cao SA bằng a, đáy ABCD là hình thang vuông tại A và B với AB bằng BC bằng a, AD bằng 2a. Trung điểm của AD được ký hiệu là E. Hãy xác định tâm và tính bán kính của mặt cầu ngoại tiếp SCDE theo a.

Lời giải

Ta có hình vẽ :

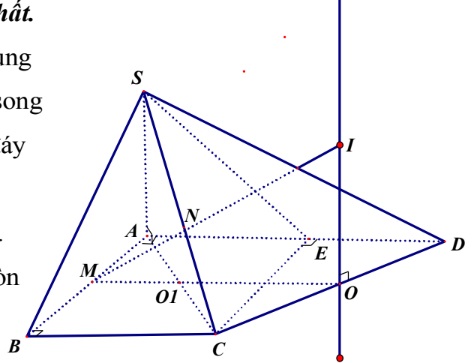
Tam giác CDE vuông tại E nên gọi O là trung điểm CD và

d là đường thẳng qua O //SA

d là trục đường tròn ngoại tiếp đáy CDE.

Gọi M, N lần lượt là trung điểm AB và SC.

Ta chứng minh được MN là trục đường tròn ngoại tiếp tam giác SEC

Vận dụng bài tập về nhà tự làm

Từ những công thức và các dạng bài tập trên bạn hãy thử làm những bài tập vận dụng để có thể nắm chắc kiến thức hơn.

Câu 1: Cho hình chóp S ABC có SA SB SC đôi một vuông góc nhau SA=a, SB=2a, SC=3a. Tính diện tích mặt cầu ngoại tiếp hình chóp S ABC

Câu 2: Hình chóp SABC có đáy là tam giác vuông cân tại B, AB=a và SA vuông góc với đáy. Hình chiếu vuông góc của A trên SB và SC lần lượt là H và K. Hãy tính bán kính mặt cầu ngoại tiếp hình chóp A.HKCB.

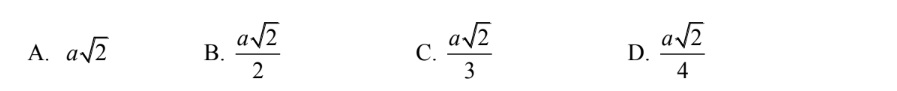
Câu 3: Hình chóp S. ABCD có đáy là hình vuông cạnh a. Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Hãy tính bán kính của mặt cầu ngoại tiếp hình chóp S ABCD.

Kết luận

Những thông tin và bài tập về mặt cầu ngoại tiếp hình chóp mà thầy muốn gửi đến các em học sinh. Để dành được điểm tuyệt đối ở dạng bài tập này đòi hỏi các em phải lưu ý và nắm vững những công thức của bài. Vậy nên hãy truy cập vào trang web của thayphu để có thể hiểu rõ bài học hơn nhé!