Giới thiệu hình trụ toán lớp 5 và bài tập áp dụng

Giới thiệu hình trụ toán lớp 5 là một hình học không gian có dạng được xác định bằng diện tích đáy nhân chiều cao. Hãy cùng chúng tôi tìm hiểu về hình này và bài tập áp dụng nhé.

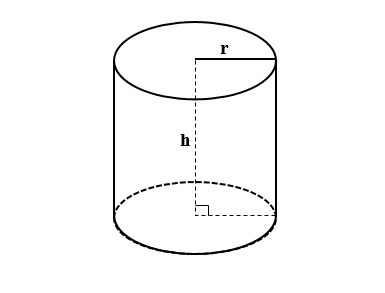
Giới thiệu hình trụ toán 5 là gì? Định nghĩa ví dụ minh họa và bài tập áp dụng

Chúng là hình học ba chiều có nhiều ứng dụng trong đời sống và các lĩnh vực khác như khoa học, kỹ thuật, nghệ thuật. Trong bài viết này của thayphu chúng ta sẽ cùng tìm hiểu về giới thiệu hình trụ đặc điểm, công thức tính toán và ứng dụng của hình trụ.

Định nghĩa về hình trụ

Chúng là một hình học không gian có dạng trụ, được hình thành bởi việc quay một hình chữ nhật quanh một trục cố định. Chính vì vậy, hình trụ có các đặc điểm sau:

• Có 2 mặt đáy hình tròn, bằng nhau và song song.
• Thân của hình trụ có dạng một hình chữ nhật.
• Gồm 3 thành phần chính: 2 mặt đáy hình tròn và 1 mặt bao hình chữ nhật.
• Chiều dài của hình trụ được gọi là chiều cao (h).
• Đường kính của 2 mặt đáy hình tròn được gọi là đường kính (d) hoặc bán kính (r).

Ví dụ: π ×2^2 ×5= 62.8

Hình trụ có rất nhiều ứng dụng trong các lĩnh vực như kiến trúc, kỹ thuật, y học, nghệ thuật và đời sống hàng ngày.

Tính chất của một hình trụ

Khi làm việc với hình trụ ta cần nắm vững tính chất để giải các bài toán liên quan. Dưới đây chúng tôi đã tổng hợp những tính chất mà bạn có thể nắm rõ

Tính đối xứng trục

Hình trụ có tính đối xứng khi ta quay chúng xung quanh trục đối xứng của nó.

Khi ta quay chung quanh trục đối xứng thì hình dạng của nó không thay đổi.

Tính trọng tâm

Hình trụ luôn có trọng tâm nên trọng tâm được tính bằng nửa cạnh đáy.

Tổng hợp công thức tính hình trụ

Tổng hợp công thức tính hình trụ

Để tính thể tích của ta sử dụng công thức sau:

V = π × r^2 × h

Trong đó:

V là thể tích của hình trụ

π (pi) là số pi, bằng khoảng 3,14159

r là bán kính đáy (hoặc đỉnh) của hình trụ

h là chiều cao của hình trụ

Ví dụ: Giả sử có một hình trụ với bán kính đáy là 5 cm và chiều cao là 10 cm. Để tính thể tích của hình trụ này, ta sử dụng công thức:

V = π × r^2 × h

V = 3,14159 × (5 cm)^2 × 10 cm

V = 3,14159 × 25 cm^2 × 10 cm

V = 785,398 cm^3

Các dạng bài tập về giới thiệu hình trụ toán lớp 5

Bạn cần nắm vững những dạng toán thường hay gặp về hình trụ. Dưới đây chúng tôi đã tổng hợp những dạng mà bạn không thể bỏ qua

Dạng 1: Tính diện tích mặt bên (xung quanh)

Công thức: A = 2πrh

Ví dụ: Tính diện tích mặt bên của hình trụ có bán kính 5cm và chiều cao 12cm.

Hướng dẫn:

Thế các giá trị vào công thức:

A = 2πrh

A = 2 x 3,14 x 5cm x 12cm

A = 376,8 cm²

Dạng 2: Tính diện tích toàn phần

Công thức: A = 2πr(h + r)

Ví dụ: Tính diện tích toàn phần của hình trụ có bán kính 7cm và chiều cao 15cm.

Hướng dẫn:

Thế các giá trị vào công thức:

A = 2πr(h + r)

A = 2 x 3,14 x 7cm x (15cm + 7cm)

A = 706,8 cm²

Đáp án: Diện tích toàn phần của hình trụ là 706,8 cm².

Dạng 3: Tính thể tích

Công thức: V = πr²h

Ví dụ: Tính thể tích của hình trụ có bán kính đáy 6cm và chiều cao 10cm.

Hướng dẫn:

Thế các giá trị vào công thức:

V = πr²h

V = 3,14 x 6²cm x 10cm

V = 1884 cm³

Đáp án: Thể tích của hình trụ là 1884 cm³.

Dạng 4: Tìm chiều cao khi biết diện tích toàn phần và bán kính

Công thức: h = (A/2πr) - r

Ví dụ: Một hình trụ có diện tích toàn phần 565,2 cm² và bán kính 6cm. Tính chiều cao.

Hướng dẫn:

Thế các giá trị vào công thức:

h = (A/2πr) - r

h = (565,2 cm²/2 x 3,14 x 6cm) - 6cm

h = 10cm

Đáp án: Chiều cao của hình trụ là 10cm.

Dạng 5: Tìm bán kính khi biết thể tích và chiều cao

Công thức: r =(V/πh)^(1/2)

Ví dụ: Một hình trụ có thể tích 3848 cm³ và chiều cao 14cm. Tính bán kính.

Hướng dẫn:

Thế các giá trị vào công thức:

r = (V/πh)^(1/2)

r = (3848 cm³/(3,14 x 14cm))^(1/2)

r = 7cm

Đáp án: Bán kính của hình trụ là 7cm.

Bài tập áp dụng về giới thiệu hình trụ toán lớp 5

Câu 1: Một hình trụ có bán kính đáy 5 cm và chiều cao 12 cm. Tính diện tích mặt bên của hình trụ.

A) 376,99 cm2

B) 188,49 cm2

C) 150,79 cm2

D) 377,00 cm2

Đáp án: A) 376,99 cm2

Câu 2: Một hình trụ có bán kính 7 cm và chiều cao 10 cm. Tính diện tích toàn phần của hình trụ.

A) 616,13 cm2

B) 308,07 cm2

C) 530,93 cm2

D) 615,75 cm2

Đáp án: D) 615,75 cm2

Câu 3: Một hình trụ có bán kính 4 cm và chiều cao 8 cm. Tính thể tích của hình trụ.

A) 201,06 cm3

B) 100,53 cm3

C) 401,12 cm3

D) 402,12 cm3

Đáp án: A) 201,06 cm3

Câu 4: Một hình trụ có diện tích mặt bên 314 cm2 và chiều cao 7 cm. Tính bán kính của hình trụ.

A) 7 cm

B) 5 cm

C) 10 cm

D) 14 cm

Đáp án: B) 5 cm

Câu 5: Một hình trụ có diện tích toàn phần 940,86 cm2 và bán kính 7 cm. Tính chiều cao của hình trụ.

A) 10 cm

B) 15 cm

C) 20 cm

D) 25 cm

Đáp án: A) 10 cm

Câu 6: Một thùng hình trụ có bán kính 12 cm và chiều cao 20 cm. Biết thể tích của một lon nước ngọt là 355 ml. Tính số lon nước ngọt có thể chứa trong thùng.

A) 50 lon

B) 75 lon

C) 100 lon

D) 125 lon

Đáp án: C) 100 lon

Câu 7: Một hình trụ có diện tích mặt bên 942,48 cm2 và bán kính 11 cm. Tính thể tích của hình trụ.

A) 1452 cm3

B) 2904 cm3

C) 3630 cm3

D) 4356 cm3

Đáp án: C) 3630 cm3

Câu 8: Một hình trụ có diện tích toàn phần 1256,64 cm2 và bán kính 8 cm. Tính thể tích của hình trụ.

A) 402,12 cm3

B) 603,18 cm3

C) 804,24 cm3

D) 1005,30 cm3

Đáp án: B) 603,18 cm3

Câu 9: Một hình trụ có diện tích toàn phần 754 cm2 và bán kính 7 cm. Tính chiều cao của hình trụ.

A) 10 cm

B) 12 cm

C) 14 cm

D) 16 cm

Đáp án: A) 10 cm

Câu 10: Một hình trụ có thể tích 1256,64 cm3 và chiều cao 12 cm. Tính diện tích mặt bên của hình trụ.

A) 502,65 cm2

B) 628,32 cm2

C) 754,00 cm2

D) 879,67 cm2

Đáp án: B) 628,32 cm2

Trên đây là một số thông tin về giới thiệu hình trụ toán lớp 5 cũng như bài tập hi vọng những thông tin này giúp bạn nắm vững rõ định nghĩa cũng như thành thạo trong các bài tập.