Giới thiệu hình cầu toán lớp 5, cách tính và bài tập áp dụng

Giới thiệu hình cầu toán lớp 5 được xác định bằng một điểm cho trước (tâm mặt cầu) và một bán kính. Hãy cùng chúng tôi tìm hiểu về định nghĩa, ví dụ và bài tập áp dụng.

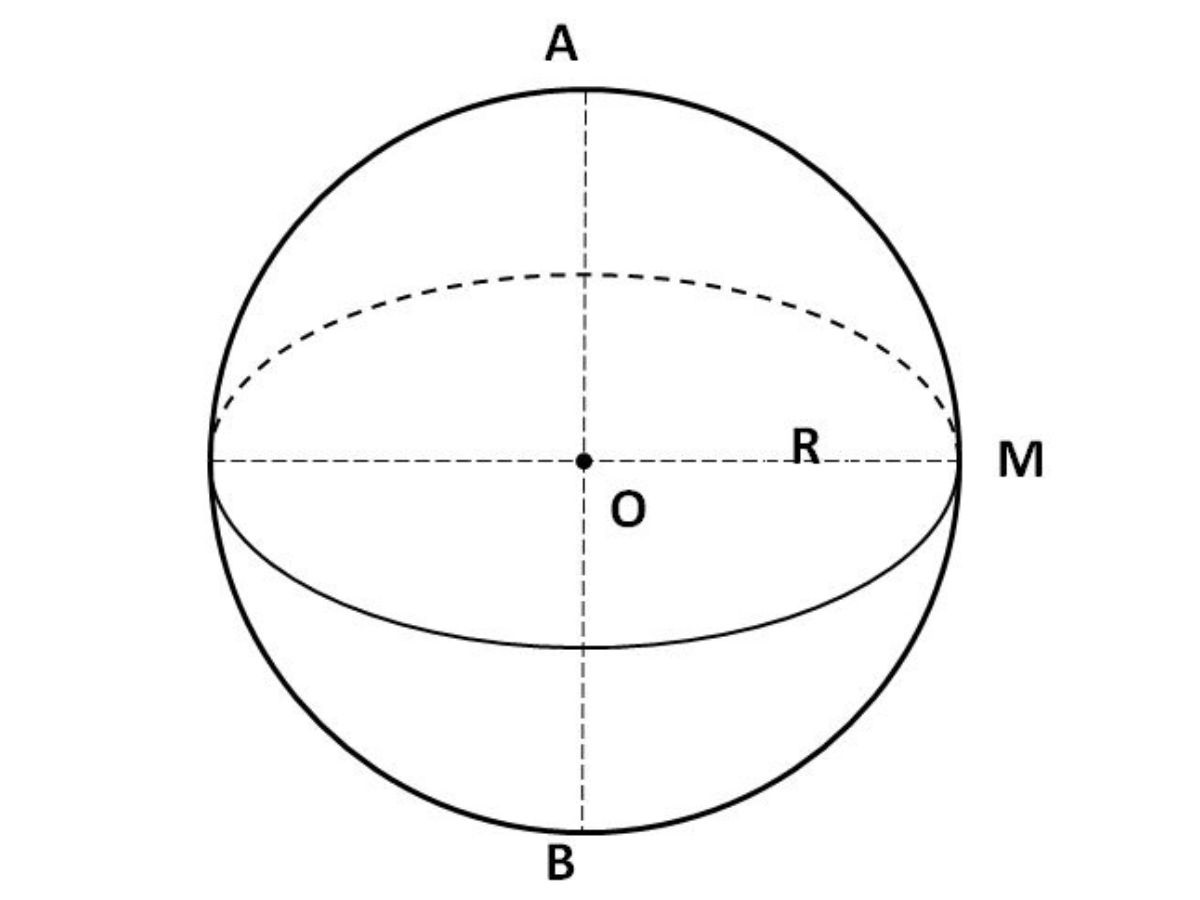
Giới thiệu hình cầu toán 5 là gì? Định nghĩa và bài tập áp dụng

Chúng là một trong những hình học quen thuộc trong toán học. Với dạng hình tròn và tính đối xứng cao, hình cầu được ứng dụng rộng rãi trong nhiều lĩnh vực như kiến trúc, kỹ thuật, thiên văn học và thậm chí cả trong nghệ thuật. Trong bài viết này của thayphu chúng ta sẽ khám phá về giới thiệu hình cầu định nghĩa ví dụ minh họa và bài tập áp dụng.

Định nghĩa về hình cầu

Theo định nghĩa, chúng là một hình học thể ba chiều, được xác định bởi tất cả các điểm cách một điểm cho trước (tâm cầu) và một khoảng cách nhất định (bán kính cầu)

Chúng được bằng cách lấy 4/3 × π × R^3

Ví dụ: Cho hình cầu có bán kính r = 7 cm.

Thể tích mặt cầu:

V = (4/3)πr^3

V = (4/3)π(7^3)

V = (4/3)π(343)

V = 2,855 × 3,14159 × 343

V = 4,188 × 10^3 cm^3

Các ứng dụng của giới thiệu hình cầu toán lớp 5

Chúng có nhiều ứng dụng trong cuộc sống và trong các lĩnh vực khoa học, công nghệ, kỹ thuật, v.v. Dưới đây là một số ứng dụng chính của hình cầu:

Trong xây dựng và kiến trúc

Các công trình kiến trúc như nhà đền, nhà thờ, nhà hát có nhiều phần dạng cầu như mái vòm, tháp chuông.

Các kết cấu cầu như cầu vượt, nhà ga, nhà máy điện.

Trong thiết bị và dụng cụ

Bóng đèn, dụng cụ quang học như kính lúp, ống kính máy ảnh.

Các thiết bị công nghiệp như bồn chứa khí, bình nước nóng.

Trong thiên văn và địa lý

Mô hình Trái Đất, Mặt Trăng, các hành tinh khác dạng cầu.

Các công trình thiên văn như đài quan sát, kính thiên văn.

Trong y học và sinh học

Mô hình các tế bào, cấu trúc sinh học dạng cầu như tế bào máu, vi khuẩn.

Các thiết bị y tế như máy X-quang, máy MRI.

Trong khoa học vật liệu

Các vật liệu dạng cầu như hạt nano, hạt nano carbon (fullerene).

Cấu trúc của các tinh thể, pha tổng hợp.

Trong công nghệ thông tin

Các ăng-ten, đầu dò sóng dạng cầu.

Các thiết bị công nghệ như loa, micro, loa phát thanh.

Các tính chất của hình cầu

Chúng có nhiều tính chất quan trọng dưới đây là những tính chất mà bạn cần nắm vững

Tính đối xứng

Hình cầu có tính đối xứng xung quanh tâm cầu.

Mọi điểm trên bề mặt cầu cách tâm cầu một khoảng cách bằng nhau (bán kính).

Tâm và bán kính

Hình cầu được xác định bởi một điểm gọi là tâm cầu.

Khoảng cách từ tâm cầu đến bất kỳ điểm nào trên bề mặt cầu được gọi là bán kính cầu.

Đường trung bình

Mọi đường thẳng đi qua tâm cầu đều được gọi là đường trung bình của cầu.

Các đường trung bình của cầu đều có độ dài bằng nhau, đó là đường kính cầu.

Tiếp tuyến và pháp tuyến

Tại mỗi điểm trên bề mặt cầu, có một mặt phẳng tiếp tuyến.

Pháp tuyến tại một điểm trên bề mặt cầu là đường thẳng vuông góc với mặt phẳng tiếp tuyến tại điểm đó.

Tổng hợp công thức tính mặt cầu

Tổng hợp công thức tính mặt cầu

Thể tích: V = (4/3)πr^3

Trong đó:

V là thể tích

r là bán kính của cầu

π ≈ 3,14159

Cách tính:

• Bước 1: Xác định bán kính r .
• Bước 2: Thay giá trị r vào công thức: V = (4/3)πr^3.
• Bước 3: Tính toán giá trị của V.

Ví dụ:

Cho hình cầu có bán kính r = 6 cm.

Thể tích mặt cầu:

V = (4/3)πr^3

V = (4/3)π(6^3)

V = (4/3)π(216)

V = 2,855 × 3,14159 × 216

V = 1.937cm^3

Một số dạng bài toán về mặt cầu

Dưới đây chúng tôi đã tổng hợp những dạng toán thường hay gặp về hình cầu

Dạng 1: Tính diện tích mặt cầu

Công thức: A = 4πr^2

Ví dụ: Tính diện tích mặt cầu có bán kính 6 cm.

Giải: A = 4πr^2 = 4π(6^2) = 4π(36) = 452,39 cm^2

Dạng 2: Tính thể tích mặt cầu

Công thức: V = (4/3)πr^3

Ví dụ: Tính thể tích mặt cầu có bán kính 8 cm.

Giải: V = (4/3)πr^3 = (4/3)π(8^3) = (4/3)π(512) = 2149,77 cm^3

Dạng 3: Tìm bán kính mặt cầu khi biết diện tích

Công thức: r = √(A/4π)

Ví dụ: Tìm bán kính mặt cầu có diện tích 200 cm^2.

Giải: A = 200 cm^2 => r = √(200/4π) = 5 cm

Dạng 4: Tìm bán kính mặt cầu khi biết thể tích

Công thức: r = ³√(3V/4π)

Ví dụ: Tìm bán kính mặt cầu có thể tích 1000 cm^3.

Giải: V = 1000 cm^3 => r = ³√(3×1000/4π) = 5 cm

Dạng 5: Tính diện tích toàn phần của mặt cầu

Công thức: A_toàn phần = 4πr^2

Ví dụ: Tính diện tích toàn phần của mặt cầu có bán kính 7 m.

Giải: A_toàn phần = 4πr^2 = 4π(7^2) = 615,75 m^2

Dạng 6: Tính diện tích mặt cầu được cắt bởi mặt phẳng

Công thức: A_cắt = πr^2

Ví dụ: Tính diện tích mặt cầu được cắt bởi mặt phẳng cách tâm 5 cm.

Giải: A_cắt = πr^2 = π(5^2) = 78,54 cm^2

Dạng 3: Tính diện tích mặt cầu bên trong hình trụ

Công thức: A_cầu = 2πrh + 4πr^2

Ví dụ: Tính diện tích mặt cầu bên trong hình trụ có bán kính 4 cm và chiều cao 10 cm.

Giải: A_cầu = 2πrh + 4πr^2 = 2π(4)(10) + 4π(4^2) = 251,20 + 200,96 = 452,16 cm^2

Bài tập áp dụng về giới thiệu hình cầu toán lớp 5

Câu 1: Tính diện tích mặt cầu có bán kính 12 cm.

A) 288π cm²

B) 576π cm²

C) 1152π cm²

D) 2304π cm²

Đáp án: B) 576π cm²

Câu 2: Tính thể tích mặt cầu có bán kính 5 m.

A) 500π m³

B) 1000π m³

C) 2000π m³

D) 4000π m³

Đáp án: C) 2000π m³

Câu 3: Tìm bán kính mặt cầu có diện tích 100 m².

A) 5 m

B) 10 m

C) 15 m

D) 20 m

Đáp án: A) 5 m

Câu 4: Tìm bán kính mặt cầu có thể tích 1000 cm³.

A) 5 cm

B) 10 cm

C) 15 cm

D) 20 cm

Đáp án: B) 10 cm

Câu 5: Tính diện tích toàn phần của mặt cầu có bán kính 8 m.

A) 256π m²

B) 512π m²

C) 1024π m²

D) 2048π m²

Đáp án: B) 512π m²

Câu 6: Tính diện tích mặt cầu được cắt bởi mặt phẳng cách tâm 7 cm.

A) 49π cm²

B) 98π cm²

C) 147π cm²

D) 196π cm²

Đáp án: A) 49π cm²

Câu 7: Tính diện tích mặt cầu bên trong hình trụ có bán kính 6 m và chiều cao 10 m.

A) 600π m²

B) 700π m²

C) 800π m²

D) 900π m²

Đáp án: D) 900π m²

Câu 8: Mặt cầu có bán kính 7 cm. Tìm thể tích phần mặt cầu nằm bên trong hình trụ có bán kính 5 cm và chiều cao 10 cm.

A) 100π cm³

B) 200π cm³

C) 300π cm³

D) 400π cm³

Đáp án: C) 300π cm³

Câu 9: Một hình cầu có diện tích toàn phần là 576π m². Tính bán kính của hình cầu.

A) 6 m

B) 8 m

C) 10 m

D) 12 m

Đáp án: B) 8 m

Câu 10: Mặt cầu có bán kính 4 cm. Tính diện tích phần mặt cầu nằm bên ngoài hình trụ có bán kính 3 cm và chiều cao 8 cm.

A) 16π cm²

B) 32π cm²

C) 48π cm²

D) 64π cm²

Đáp án: B) 32π cm²

Trên đây là một số thông tin về giới thiệu hình cầu toán lớp 5 mà thayphu.net đã thông tin đến cho bạn kèm bài tập nếu bạn còn thắc mắc vấn đề gì xin liên hệ với chúng tôi.