Nắm kiến thức điểm biểu diễn số phức trong 5 phút

Những bài toán liên quan đến điểm biểu diễn số phức thường có độ phức tạp lớn và yêu cầu học sinh phải phân biệt được từng dạng toán và cách giải của từng bài.

Điểm biểu diễn của một số phức là dạng toán tìm tập hợp điểm khá hay và hấp dẫn trong chuyên đề số phức. Một trong những phần sẽ có trong chương trình thi Trung học phổ thông quốc gia. Vậy làm thế nào để nắm chắc những kiến thức và giải được các bài toán về điểm biểu diễn số phức một cách nhanh nhất? Hãy cùng thayphu giúp các em thực hiện điều này qua bài viết nhé.

Điểm biểu diễn số phức là gì?

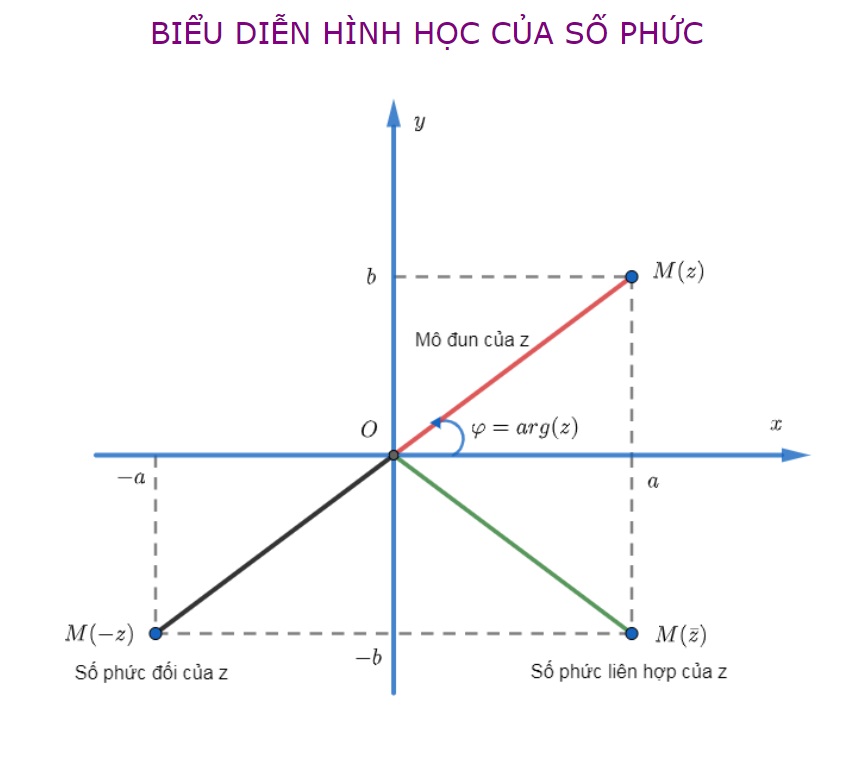
Định nghĩa về điểm biểu diễn của một số phức z

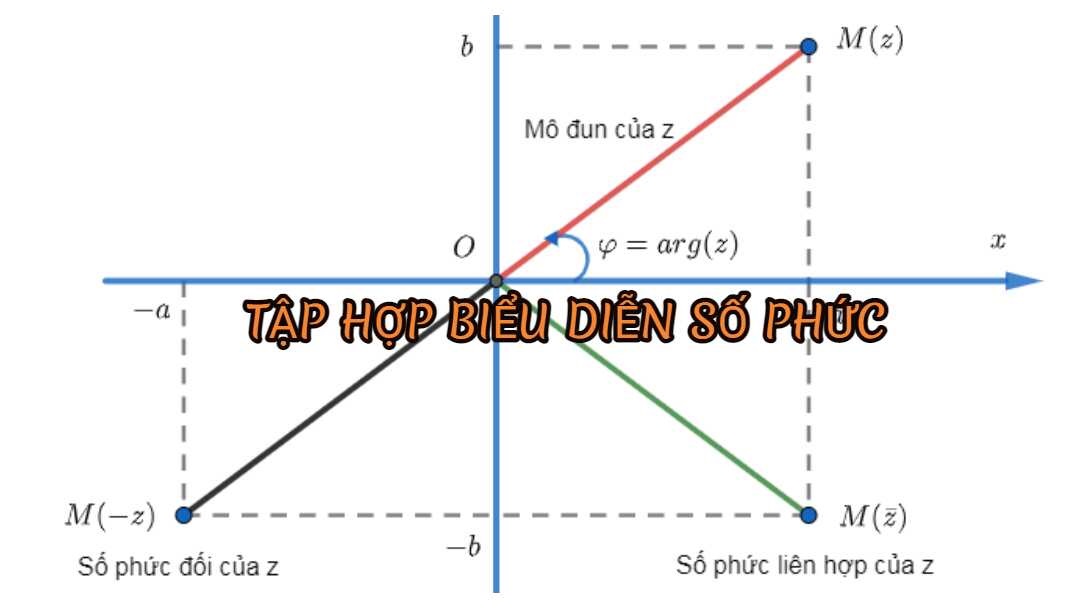
Điểm biểu diễn số phức hay điểm biểu diễn hình học của số phức được định nghĩa như sau: Mỗi số phức z = a+bi (a, b thuộc R) được biểu diễn bằng một điểm A (a,b) khi đó vectơ OA→= (a, b) trên mặt phẳng phức.

Khi đó ta có điểm A có toạ độ là (a, b) ký hiệu A (a,b) hay A (z). Tập hợp các điểm biểu diễn số phức tương ứng lên mặt phẳng sẽ có những khái niệm đi kèm như sau:

• Phần thực của số phức z là hoàn độ của điểm A (z)
• Phần ảo của số phức z là tung độ của điểm A (z)
• Mô đun của số phức là độ dài của đoạn thẳng OM (z), trong đó O là gốc toạ độ. Từ đó ta có thể suy ra: |z| = |OA→| = a2 + b2

Nếu điểm A (z1) là điểm biểu diễn của số phức z1 và B (z2) là điểm biểu diễn của số phức z2. Thì:

z1 - z2 = OA→ - OB→ = BA→

z1 + z2 = OA→ + OB→

• Điểm biểu diễn số phức liên hợp của số phức z chính là điểm đối xứng của A (z) qua trục thực.

Một số dạng toán thường gặp về điểm biểu diễn số phức

Những dạng toán thường gặp về điểm biểu diễn của số phức z

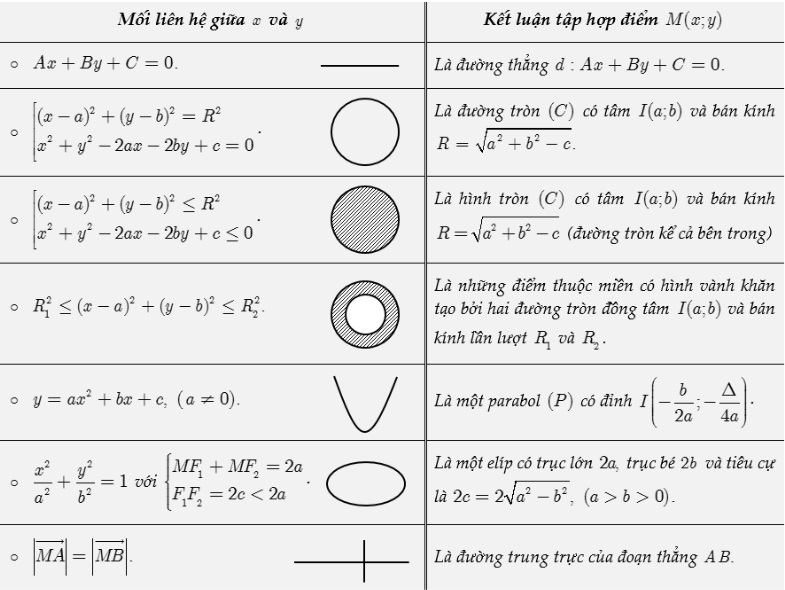
Dù là một phương trình, hệ phương trình hay bất phương trình (phức) cũng sẽ tương ứng cho ra một hình nào đó ở trên mặt phẳng phức. Từ đó, chúng ta có những bài toán xác định các điểm biểu diễn số phức thoả mãn điều kiện cho trước. Một số dạng toán thường gặp khi biểu diễn hình học số phức như sau:

Dạng 1: Điểm biểu diễn của tập hợp số phức là một đường thẳng

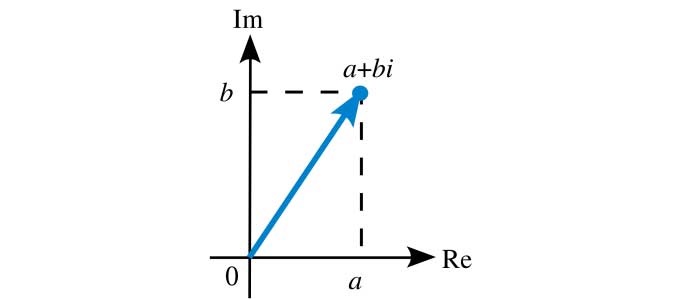
Lý thuyết: Cho số phức z = a + bi ( với a, b thuộc R), ta có điểm M (a,b) là điểm biểu diễn của số phức z thoả mãn điều kiện cho trước.

Nếu ta biến đối điều kiện và tìm được mối liên hệ giữa a và b có dạng Aa + Bb + C = 0. Ta kết luận tập hợp điểm biểu diễn của số phức Z là một đường thẳng d: Aa + Bb + C =0.

Ví dụ minh hoạ: Tập hợp điểm biểu diễn số phức z thoả mãn điều kiện | z - (1 + i) = | z + 2i| là một đường thẳng. Hãy tìm đường thẳng đó.

Bài làm:

Gọi số phức z = a + bi (a, b thuộc R) được biểu diễn bởi điểm M (a, b) trong mặt phẳng Oxy.

Ta có | z - (1 + i) = | z + 2i| | a + bi - (1 + i) = | a+ bi + 2i|

(a-1)2 + (b-1)2=a2 + (b+2)2

(a-1)2 + (b-1)2 = a2 + (b+2)2

a2 - 2a + 1 + b2 - 2b + 1 = a2 + b2 + 2b + 4

a+ 3b + 1 = 0

Suy ra, tập biểu diễn của số phức z là đường thẳng a + 3b + 1 = 0.

Dạng 2: Điểm biểu diễn của tập hợp số phức là một đường tròn

Lý thuyết: Cho số phức z = a + bi ( với a, b thuộc R), ta có điểm M (a,b) là điểm biểu diễn của số phức z thoả mãn điều kiện cho trước.

Nếu ta biến đối điều kiện và tìm được mối liên hệ giữa a và b có dạng:

(a - x)2 + (b - y)2 = R2

Ta kết luận điểm biểu diễn của tập hợp số phức là đường tròn tâm I (x, y) với bán kính R.

Ví dụ minh hoạ: Tập hợp các điểm M thoả mãn | z - 2 + 5i| = 4 là một đường tròn. Hãy tìm toạ độ tâm I và bán kính của đường tròn đó.

Bài làm:

Gọi số phức z = a + bi (a, b thuộc R), ta có: | z - 2 + 5i| = 4

| a + bi - 2 + 5i| = 4

(a-2)2 + (b + 5)2 = 4

(a-2)2 + (b + 5)2 = 42

Kết luận: Tập hợp điểm biểu diễn số phức z là đường tròn tâm I ( 2, -5) với bán kính bằng 4.

Dạng 3: Điểm biểu diễn của tập hợp số phức là một miền

Lý thuyết: Cho số phức z = a + bi ( với a, b thuộc R). Miền biểu diễn tập hợp số phức là những điểm thuộc miền có hình vành khăn được tạo bởi 2 đường tròn cùng tâm I (x, y) với bán kính lần lượt là R1và R2. Khi đó, mối liên hệ giữa a và b là R12 (a - x)2 + (b - y)2 R22

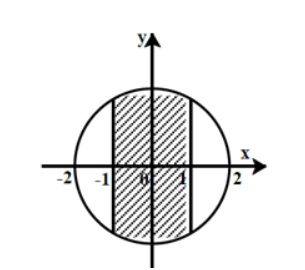
Ví dụ minh hoạ: Cho số phức z = a+ bi có điểm biểu diễn số phức như hình vẽ thì phải thoả mãn điều kiện gì?

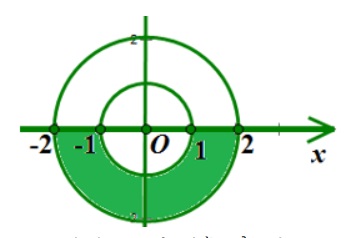
Ta thấy, phần tô màu dưới trực hoành là hình vành khăn và được tạo bởi 2 đường tròn chung tâm 0 (0;0) với bán kính lần lượt là R1= 1 và R2= 2.

Đây là tập hợp các điểm M (a; b) biểu diễn số phức z = a + bi trong mặt phẳng phức thoả mãn 1 (a - 0)2 + (b - 0)2 2 với phần ảo âm.

Dạng 4: Điểm biểu diễn của tập hợp số phức là một đường conic

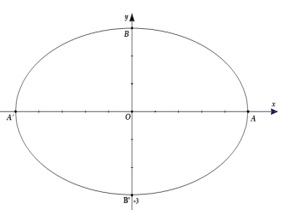
Lý thuyết: Đường conic là đường cong bậc 2 được tạo ra bằng cách cắt một mặt nón tròn xoay bằng 1 mặt phẳng. Trong toán học, chúng ta sẽ gặp một số hình conic như elip, parabol,... Sau khi biến đổi điều kiện ban đầu và tìm được mối liên hệ của a, b về dạng:

• y = Aa2 + Bb + C thì tập hợp điểm biểu diễn của số phức z = a+ bi là một đường Parabol có đỉnh I (- B2A , - 4A ).
• a2A2 + b2B2 = 1 với MF1 +MF2 = 2A và F1F2 = 2C < 2 A. Lúc này, tập hợp điểm biểu diễn số phức z = a + bi là một hình elip có trục lớn bằng 2A và trục bé bằng 2B với tiêu cự F1F2 = 2C = 2(A2-B2 ( với A > B > 0).

Ví dụ 1: Tập hợp các điểm M biểu diễn số phức z thoả mãn điều kiện sau: 2| z - i| = |z - z + 2i | là một hình parabol.

Bài làm:

Gọi số phức z có dạng z = a+ bi, suy ra z =a -bi

Ta có: 2 | z - i| = |z - z + 2i |

2 | a + bi - i| = |a + bi - (a - bi)+ 2i |

2(a2 + (b-1)2=2(b + 1)2

a2 + b2 - 2b + 1 = b2 +2b + 1

a2 =4b

b = 14a2

Kết luận: Vậy tập hợp điểm biểu diễn số phức thoả mãn điều kiện trên là một parabol có phương trình b = 14a2 .

Phương pháp giải bài toán về điểm biểu diễn số phức

Cách giải từng dạng toán về tập hợp các điểm biểu diễn một số phức

Trong chương trình học và thi Trung học phổ thông Quốc gia, các em chủ yếu gặp dạng toán điểm biểu diễn số phức là đường thẳng và đường tròn. Vậy nên, trong bài viết này, thayphu.net sẽ tập trung vào 2 nội dung trên:

Bài toán 1: Tìm tập hợp điểm biểu diễn số phức z = a + bi thoả mãn | z - (a + bi)| = R

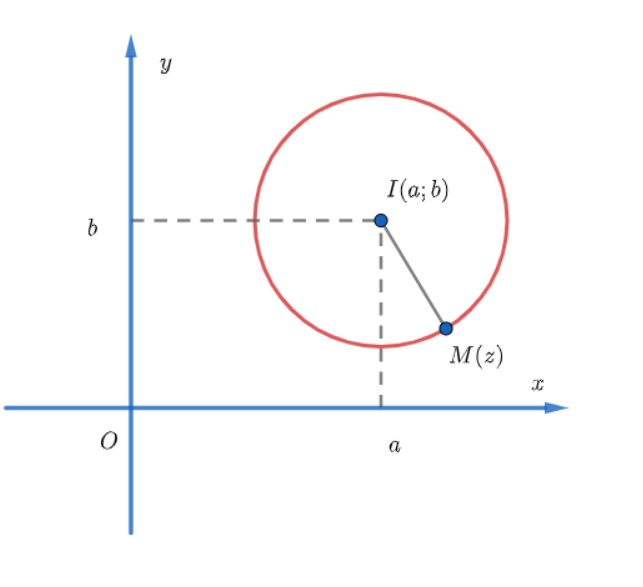
Tập hợp các điểm biểu diễn số phức trong bài toán này là một đường tròn có tâm I(a,b) và bán kính R. Đối với bài toán này, ta có 2 cách giải như sau:

Cách 1: Biến đổi phương trình đề bài cho và lấy mô đun hai vế

Ví dụ minh hoạ: Cho số phức z = a + bi thoả mãn |z - 3i + 2| = 3 là một đường tròn, biết tập hợp các điểm biểu diễn của số phức w = (3 + 4i) z + 4 - 6i. Tìm tâm và bán kính đường tròn biểu diễn số phức w.

Bài làm:

Ta có:

• w = (3 + 4i) z + 4 - 6i
• w = (3 + 4i)(z - 3i + 2 + 3i - 2) + 4 - 6i
• w = (3 + 4i)(z - 3i + 2) + (3 + 4i)( 3i - 2) + 4 - 6i
• w = (3 + 4i)(z - 3i + 2) + 9i - 6 - 12 - 8i + 4 - 6
• w - 20 + i = (3 + 4i)(z - 3i + 2)

Lấy mô đun 2 vế: |w - 20 + i| = |(3 + 4i)|.|(z - 3i + 2)|

|w - 20 + i| = 5. 3 = 15

Vậy điểm biểu diễn số phức w là đường tròn tâm I (20, -1 ) với bán kính R = 15.

Cách 2: Cách giải nhanh

Ta có M(z) là điểm biểu diễn số phức z, thì

• Điểm M( z + (a + bi)) được thực hiện bằng cách tính tiến điểm M (z) theo vectơ có toạ độ (a, b). Trong đó, phép tịnh tiến sẽ biến một đường tròn thành một đường tròn khác có cùng bán kính và biến tâm thành tâm.
• Điểm M (z.(a+bi) được thực hiện bằng cách thực hiện phép quay tâm O, sau đó vị tự tâm O với tỷ số | a + bi|. Trong đó, phép vị tự tỷ số K sẽ biến đường tròn có bán kính R thành một đường tròn khác có bán kính là |k|R và biến tâm thành tâm.

Ví dụ minh hoạ: Tương tự ví dụ trên, ta sẽ có cách giải nhanh như sau:

Tâm đường tròn biểu diễn số phức z có tâm I( -2, 3).

Đông thời tịnh tiến và vị tự đường tròn biểu diễn điểm z để tạo thành đường tròn biểu diễn điểm w ta có: (3 + 4i)(2 - 3i) + 4 - 6i = 20 - i. Suy ra, tâm đường tròn biểu diễn w là I( 20, -1).

Bán kính của đường tròn biểu diễn z là 3, suy ra bán kính của đường tròn biểu diễn w là | 3 + 4i|.3 = 15.

Bài toán 2: Tìm tập hợp điểm biểu diễn số phức x thoả mãn f (z, z ) là số thực hoặc là số ảo, hoặc f (z, z ) = g (z, z )

Để giải bài toán này, ta đặt z = a + bi với a, b thuộc R, sau đó, tìm z = a - bi. Thay z và z vào biểu thức ban đầu, biến đổi chúng nhằm tạo ra mối liên hệ giữa a, b và kết luận.

Trường hợp đặc biệt 1: Tìm điểm biểu diễn của số phức z thoả mãn |z - (m + ni)| = | z - (p +qi)|.

Cách giải: Gọi M (z), A (m,n), B(p,q) lần lượt là các điểm biểu diễn của số phức z, m + ni và p + qi. Khi đó |z - (m + ni)| = | z - (p +qi)|, suy ra MA = MB và M là đường trung trực của AB hay nói cách khác, tập hợp các điểm biểu diễn của số phức z chính là đường trung trực của AB.

Ví dụ minh hoạ: Tìm tập hợp các điểm biểu diễn của số phức z thoả mãn (z - 1)(z + 1) là 1 số thực.

Bài giải:

Đặt z = a + bi, suy ra z = a - bi

Ta có: (z - 1)(z + 1) = (a + bi - 1)( a - bi + 1) = [(a - 1)+ bi].[(a + 1) - bi]

= (a - 1)(a + 1) + b 2 + [(a - 1) (-b) + b (a + 1)]i

Để (z - 1)(z + 1) là 1 số thực thì [(a - 1) (-b) + b (a + 1)] = 0

-ab + b + ab + b = 0 2b = 0 b = 0.

Kết luận: Vậy điểm biểu diễn của số phức z là đường thẳng b = 0 thì (z - 1)(z + 1) là 1 số thực.

Bài toán 3: Tìm tập hợp các điểm biểu diễn của số phức z thoả mãn |z - (m + ni)| + | z - (p +qi)| = 2a là một đường elip.

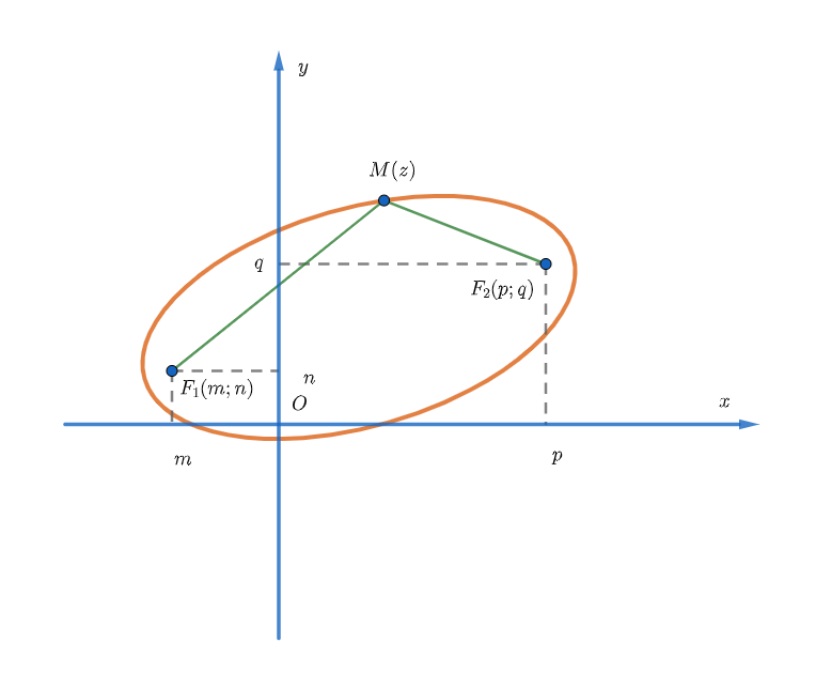
Điểm biểu diễn số phức z là đường elip có 2 tiêu điểm toạ độ là F1(m,n) và F2 (p,q) với độ dài trục lớn bằng 2a. Từ dữ kiện trên, sẽ có những bài toán mở rộng hơn và tuỳ vào từng câu hỏi cụ thể, các em sẽ tìm đáp án theo đề bài.

Ví dụ minh hoạ: Cho số phức thoả mãn điều kiện |z + 2| + |z - 2| = 10 là một hình elip. Xác định toạ độ 2 tiêu điểm và tìm giá trị M + n. Trong đó, M và n lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của |z|.

Bài làm:

Ta có: toạ độ tiêu điểm là F1 (-2, 0) và F2 (2, 0).

Độ dài trục lớn 2a = 10

Tiêu cự 2c = F1.F2 = 4

Độ dài trục bé: b = a2- c2 = 21

Suy ra, M = a = 5, n = b = 21. Vậy M + n = 5 + 21

Bài toán 4: Tìm tập hợp điểm biểu diễn của số phức w = z1.z + z2 thoả mãn |z - (a + bi)| = R (R>0).

Cách giải: Gọi M (z) và I(a, b) lần lượt là các điểm biểu diễn của số phức z và (a + bi). Ta có: w = z1.z + z2, suy ra z = w- z2z1

Lại có: |z - (a + bi)| = R | w- z2z1 - a - bi| = R | w - z2 - z1 (a + bi)| = |z1|R

Vậy tập hơp các điểm biểu diễn số phức w là một đường tròn tâm I (a, b) có bán kính |z1|R.

Lưu ý: Nếu thêm yếu tố z0 thì bán kính đường tròn sẽ thay đổi thành | z1||z0|R.

Ví dụ minh hoạ: Tìm tập hợp điểm biểu diễn của số phức w = (3 - 2i)z + 5 + 3i thoả mãn | z - 2i| = 4

Bài làm:

Gọi M (z) là điểm biểu diễn của số phức z. Ta có: w = (3 - 2i)z + 5 + 3i, suy ra z = w- 5-3i3-2i

Lại có: | z - 2i| = 4 | w- 5-3i3-2i - 2i| = 4 |w - 5 - 3i - 6i - 4 | = 4|3 - 2i|

|w - 9 - 9i| = 20. Vậy tập hợp điểm biểu diễn số phức w là đường tròn tâm I (9,9) có bán kính bằng 20.

Những lưu ý về dạng bài điểm biểu diễn số phức

Lưu ý khi biểu diễn số phức

Nhằm giúp các em học sinh nắm vững được kiến thức về bài toán điểm biểu diễn số phức thì thayphu.net có những lưu ý như sau:

• Nắm chắc kiến thức và luyện tập thường xuyên để nâng cao khả năng nhận biết và giải quyết từng dạng bài.
• Đới với các điểm biểu diễn số phức thoả mãn bất phương trình | z - (a + bi)| R là một hình tròn có tâm là I(a, b) và bán kính là R ( bao gồm cả phần biên). Nếu không có dấu = thì hình tròn không bao gồm phần biên.
• Các điểm biểu diễn của số phức thoả mãn bất phương trình | z - (a + bi)| R là phần ngoài của một hình tròn có tâm là I(a, b) và bán kính là R ( bao gồm cả phần biên). Nếu không có dấu = thì hình tròn không bao gồm phần biên.

Bài tập tự luyện về điểm biểu diễn số phức

Bài tập tự luyện giúp các em tìm được vị trí các điểm biểu diễn số phức

Sau khi đã nắm được kiến thức cũng như ví dụ bài giảng thì các em có thể tự mình giải quyết thêm những bài tập dưới đây.

Bài 1: Tìm tập hợp điểm M biểu diễn số phức z = a+ bi thoả mãn:

1. 2| z - 3i| = | z - 2z + 2i|
2. | z - 2i| = | z -1|
3. | z - 2 + 3i| = | z - 4i|
4. | z + 2 + 2i| = |z - 3i|
5. |z + 2| + | z - 2| = 5
6. 2 |z - 1| = | z - z +2i|
7. 3 |z + i| = |2z - z + 3i|

Bài 2: Tìm tâm và bán kính của đường tròn trong những trường hợp sau, biết rằng:

1. Số phức z thỏa mãn |z - 2| = 2 và tập hợp các điểm biểu diễn số phức w = (1 - i)z + i.
2. Số phức z thỏa mãn |z - 4| = 6 và tập hợp các điểm biểu diễn số phức w = ( 1 + 3i)z + 5
3. Số phức thỏa mãn |z| = 2 và tập hợp các điểm biểu diễn số phức i.w = ( 3- 4i)z + 2i.

Bài 3: Tìm khoảng cách từ gốc toạ độ đến điểm M, biết tập hợp các điểm biểu diễn số phức thoả mãn ( z - 1)( z+ 2) là số thực, trong đó M là một đường thắng.

Bài 4: Tập hợp các điểm biểu diễn của số phức z là một đường tròn thoả mãn (z - 6)(8 - z .i) là một số thực. Hãy xác định tâm I (a, b), bán kính R và tìm giá trị T = a - b + R.

Kết luận

Bài viết trên thayphu.net đã tổng hợp chi tiết nội dung liên quan về điểm biểu diễn số phức. Hy vọng những kiến thức này có thể bổ trợ các em học tốt phần số phức và dễ dàng giải quyết các bài toán tìm điểm biểu diễn của các số phức trong thời gian nhanh nhất.