Công thức giải nhanh để hàm số có 3 điểm cực trị

Để hàm số có 3 cực trị là khi hàm số có tối đa hóa với 3 điểm cực trị thông qua phương pháp toán học. Dạng bài toán phổ biến được sử dụng ở các kì thi.

Hàm số là một khái niệm quan trọng và phổ biến và được sử dụng ở khắp các bài thi. Một trong những dạng toán của hàm số là các điểm cực trị, nơi mà đạo hàm của hàm số bằng 0 hoặc không tồn tại. Trong bài viết này, Thayphu sẽ cùng các em khám phá khi để hàm số có 3 cực trị là như thế nào nhé!

Khái niệm cực trị hàm số

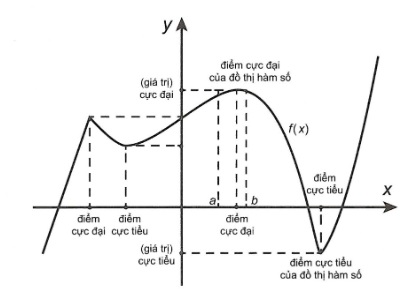
Cực trị hàm số

Cực trị của một hàm số là các điểm cực đại hoặc cực tiểu của hàm số. Nói cách khác, đó là các điểm trên đồ thị của hàm số mà giá trị của hàm số là lớn nhất hoặc nhỏ nhất so với các giá trị khác trong một vùng xung quanh.

Để tìm các điểm cực trị, ta có thể sử dụng đạo hàm của hàm số và giải phương trình đạo hàm bằng 0 hoặc xét sự biến thiên của đạo hàm xung quanh các điểm trên đồ thị. Các điểm cực trị rất quan trọng trong việc tìm kiếm giá trị cực đại hoặc cực tiểu của hàm số trong các ứng dụng thực tế.

• Giả sử hàm số f đạt cực trị tại điểm Xo . Khi đó, nếu f có đạo hàm tại điểm Xo thì f’(Xo)= 0
• Nếu f’(X) đổi dấu từ âm sang dương khi x đi qua điểm Xo (theo chiều tăng) thì hàm số đạt cực tiểu tại điểm Xo.
• Nếu f’(X) đổi dấu từ dương sang âm khi x đi qua điểm Xo (theo chiều tăng) thì hàm số đạt cực đại tại điểm Xo .
• Giả sử hàm số f có đạo hàm cấp một trên khoảng (a;b) chứa điểm Xo, f’(Xo)=0 và f có đạo hàm cấp hai khác 0 tại điểm Xo .

Điều kiện để hàm số có 3 cực trị là gì?

Để hàm số có 3 cực trị, điều kiện cần là hàm số phải có ít nhất 4 điểm uốn. Cụ thể như sau:

Xét hàm số : 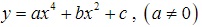hàm số có đạo hàm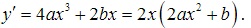

Đồ thị có 3 điểm cực trị khi và chỉ khi y’=0 có 3 nghiệm phân biệt ⇔ ab<0

Đồ thị hàm số khi có đúng một điểm cực trị hoặc 3 điểm cực trị và luôn có cực trị nằm trên trục tung

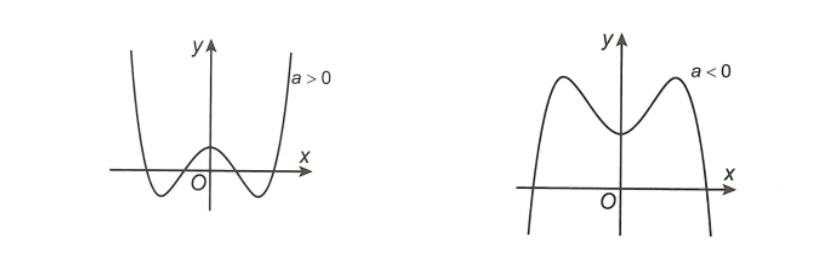
Đồ thị hàm số có 3 cực trị khi:

• Nếu a>0 hàm số có 2 điểm cực tiểu và 1 điểm cực đại
• Nếu a<0 hàm số có 2 điểm cực đại và 1 điểm cực tiểu

=> 3 điểm cực trị của đồ thị hàm số luôn tạo thành một tam giác cân

Dạng bài tập để hàm số có 3 cực trị thường gặp

Dạng 1: Tìm số nguyên trong một khoảng đồ thị

Ví dụ: Có bao nhiêu số nguyên m ε [ -20;20} đề đồ thị hàm số 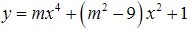có 3 điểm cực trị

Lời giải:

Ta có y’ = 4mx^3 + 2(m^2 - 9)x = 2x[ 2mx^2 + ( m^2 -9)]

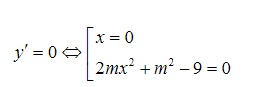=> có 2 nghiệm phân biệt khác 0

Hàm số có 3 điểm cực trị khi và chỉ khi y’=0 có 3 nghiệm phân biệt

⇔ 2m (m^2 -9)<0 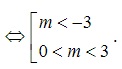=> có 19 giá trị của m để thỏa mãn

Dạng 2: Tập hợp các giá trị của m khi cho hàm số và hoành độ

Ví dụ: Tập hợp các giá trị của tham số m để đồ thị hàm số y= x^4 + 3mx^2-4 có 3 điểm cực trị phân biệt và hoành độ trong khoảng ( -2;2)

Lời giải

ta có y’ = 4x^3 + 6mx ta cho y’=0

=> ta có x=0 và 2x^2 = -3m

Để thỏa mãn đề bài có 2 nghiệm phân biệt và trong khoảng ( -2;2)

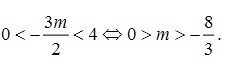
Dạng 3: Tìm tham số m để biết hàm là cực đại hay cực tiểu

Ví dụ 1: Giá trị của m để hàm số 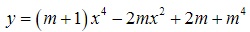đạt cực đại tại x=2

Lời giải

y’= 4(m+1)x^3 - 4mx => y” = 12(m+1)^2 - 4m

Theo đề bài x=2 để hàm số đạt cực đại thì y’ (2) = 0 => 32(m+1)-8m=0 => m = -4/3

với m = -4/3 thì y” (2) = 12(-4/3+1).2^2 - 4(-4/3)<0 => x=2 là điểm cực đại

Dạng 4: Cho hàm số, một điểm cực đại và 2 điểm cực tiểu ( ngược lại). Tìm giá trị nhỏ nhất của biểu thức

Ví dụ: Biết rằng đồ thị hàm số y= x^4 -2(m-1)x^2 +3’ có A là điểm cực đại và B , C là hai điểm cực tiểu. Tìm giá trị nhỏ nhất của biểu thức P=OA+12/BC

Trả lời

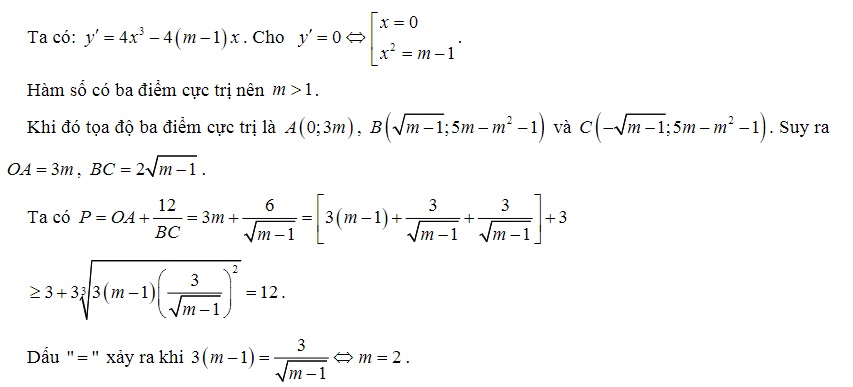
Dạng 5: Cho 2 đồ thị hàm số và tìm giá trị nguyên

Ví dụ: Cho đồ thị hàm số (C1): y= f(x) = x^4 + ax^2 +b và đồ thị hàm số (C2): y=g(x) = x^3 +mx^2 + nx+p ( như hình vẽ dưới đây). Gọi B , D là hai điểm cực tiểu của (C1) và A , C lần lượt là điểm cực đại và điểm cực tiểu của (C2). A,C đối xứng nhau qua 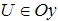. Biết hoành độ A,B bằng nhau và hoành độ của C,D bằng nhau. Có bao nhiêu giá trị nguyên của a để AB<= 3

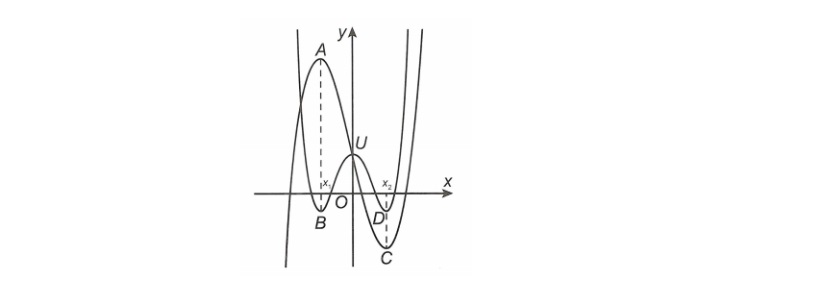
Lời giải

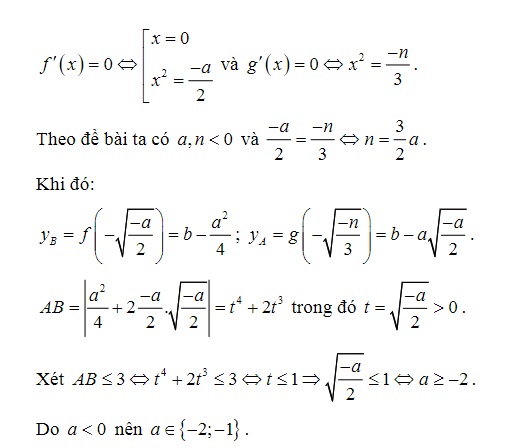
Dạng 6: Tam giác tạo bởi 3 điểm cực trị của đồ thị hàm số

Ví dụ 1: Tìm các giá trị của tham số m để đồ thị y= x^4 -2m^2x^2 + 1 có ba điểm cực trị tạo thành một tam giác vuông cân.

Lời giải

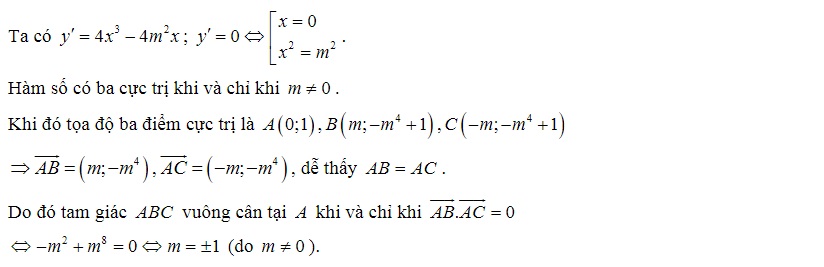
Ví dụ 2: Giá trị của tham số m để đồ thị hàm số y= x^4 - 2(m-1)x^2 +3m có ba điểm cực trị tạo thành một tam giác có góc bằng 60 độ thuộc khoảng nào?

Lời giải

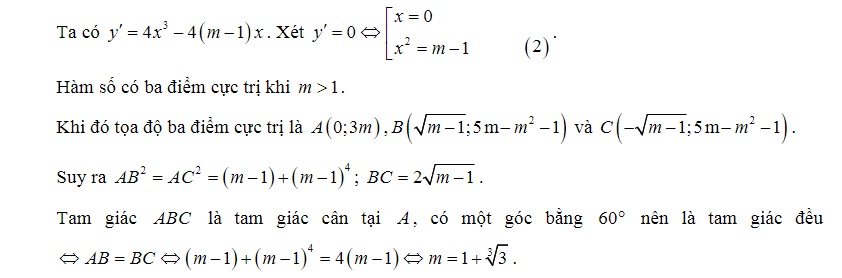
Ví dụ 3: Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số y= 2x^4 -4mx^2 +1 có 3 điểm cực trị tạo thành một tam giác có một góc bằng 30 độ.

Lời giải

y’= 6x^3 - 8mx

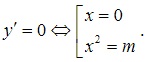
Ví dụ 4: Biết đồ thị hàm số 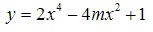có 3 điểm cực trị A ( thuộc trục tung) và B,C. Giá trị nhỏ nhất của biểu thức .

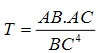Lời giải

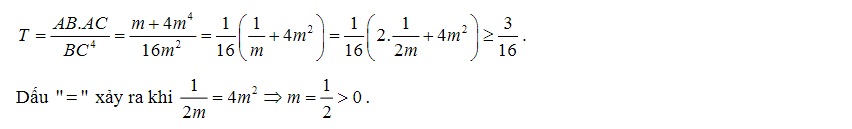
Kết luận

Để hàm số có 3 cực trị ta cần phải biến đổi và nắm chắc những công thức đang học. Từ đó áp dụng vào thực tế để có thể đạt được điểm cao trong bài thi. Nếu các bạn đang tìm kiếm những công thức về cực trị thì hay truy cập ngay vào Thayphu.net để có thể học tốt hơn nhé!