Cách tính cực trị hàm trùng phương và bài tập vận dụng

Phương pháp tính cực trị hàm trùng phương, công thức tính nhanh và các dạng bài tập vận dụng từ cơ bản đến nâng cao.

Hàm trùng phương là một dạng hàm toán học có bậc hai, trong đó biểu thức của hàm chứa các lũy thừa bậc hai của biến độc lập. Để tìm cực trị của hàm số trùng phương, chúng ta cần xác định các giá trị của biến độc lập mà hàm đạt cực đại hoặc cực tiểu.

Bài viết này, thayphu sẽ hướng dẫn chi tiết cho các bạn học sinh các điều kiện của cực trị hàm trùng phương, phương pháp tính và công thức tính nhanh siêu hay để rút gọn thời gian giải bài tập.

Hàm trùng phương là gì? Định nghĩa cơ bản

Hàm số trùng phương là hàm số bậc 4 có dạng như sau:

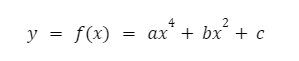
Như vậy, chúng ta cũng có thể coi hàm số trùng phương là một hàm số bậc 2 với ẩn là x^2.

Điều kiện xét cực trị hàm trùng phương

• Để xét hàm trùng phương có 3 cực trị:

Hàm số y = ax4 + bx2 + c có 3 cực trị ⇔ ab < 0

Khi đó ta suy ra:

• Hàm số có 2 cực tiểu và 1 cực đại ⇔ a > 0; b < 0
• Hàm số có 2 cực đại và 1 cực tiểu ⇔ a < 0; b > 0
• Để xét hàm trùng phương có 1 cực trị:

Hàm số y = ax4 + bx2 + c có 1 cực trị ⇔ ab ≥ 0

Khi đó ta suy ra:

• Hàm số có đúng 1 cực trị là cực tiểu ⇔ a > 0; b ≥ 0
• Hàm số có đúng 1 cực trị là cực đại ⇔ a < 0; b ≤ 0

Các bước tính cực trị hàm trùng phương cơ bản

• Bước 1: Xác định biểu thức của hàm

Xác định biểu thức chính xác của hàm số trùng phương. Biểu thức này có thể có dạng f(x) = ax^4 + bx^2 + c, trong đó a, b và c là các hằng số.

• Bước 2: Tính đạo hàm

Tính đạo hàm của hàm trùng phương bằng cách lấy đạo hàm của biểu thức hàm theo biến độc lập x. Đạo hàm này có thể được tính bằng cách áp dụng các quy tắc đạo hàm cho các thành phần của biểu thức.

• Bước 3: Giải phương trình f'(x) = 0

Để tìm các điểm cực trị, giải phương trình f'(x) = 0. Điều này đồng nghĩa với việc tìm các giá trị của biến độc lập x mà đạo hàm của hàm bằng 0.

• Bước 4: Xác định cực trị

Xác định xem các giá trị x thu được từ phương trình f'(x) = 0 có thể là cực đại hay cực tiểu bằng cách kiểm tra dấu của đạo hàm thứ hai f''(x) tại những điểm đó.

Nếu f''(x) > 0, điểm tương ứng là cực tiểu

Nếu f''(x) < 0, điểm tương ứng là cực đại.

• Bước 5: Kiểm tra biên

Kiểm tra giá trị hàm trên các giới hạn của miền xác định để xác định xem có tồn tại các cực trị ở biên của miền hay không.

• Bước 6: Vẽ đồ thị

Dựa trên các giá trị cực trị đã tìm được và kiểm tra biên, vẽ đồ thị của hàm trùng phương để hiển thị các điểm cực đại và cực tiểu.

• Dưới đây là bài tập ví dụ để các bạn học sinh có thể hiểu rõ hơn về các bước tính cực trị hàm trùng phương

Xét hàm trùng phương f(x) = ax^4 + bx^2 + c với a = 1, b = -2, và c = 3.

• Bước 1: Biểu diễn hàm: f(x) = x^4 - 2x^2 + 3.
• Bước 2: Tính đạo hàm: f’(x) = 4x^3 - 4x.
• Bước 3: Giải phương trình f’(x) = 0:

⇔ 4x^3 - 4x = 0

⇔ 4x(x^2 - 1) = 0

⇔ 4x(x + 1)(x - 1) = 0

Có ba giá trị x tương ứng: x = 0, x = -1, và x = 1.

• Bước 4: Xác định cực trị:

Ta có đạo hàm của f’(x) là f’’(x) = 12x^2 - 4.

Để xác định xem các giá trị x tìm được có phải là cực đại hay cực tiểu, ta kiểm tra dấu của f’’(x) tại những điểm đó.

Với x = 0: f’’(0) = -4 < 0, nên x = 0 là điểm cực đại.

Với x = -1: f’’(-1) = 8 > 0, nên x = -1 là điểm cực tiểu.

Với x = 1: f’’(1) = 8 > 0, nên x = 1 là điểm cực tiểu.

• Bước 5: Kiểm tra biên:

Xét giá trị hàm trên giới hạn của miền xác định:

Khi x tiến tới âm vô cùng, hàm tăng không giới hạn.

Khi x tiến tới dương vô cùng, hàm tăng không giới hạn.

• Bước 6: Vẽ đồ thị:

Vẽ đồ thị hàm trùng phương để hiển thị hình dạng và các điểm cực đại và cực tiểu.

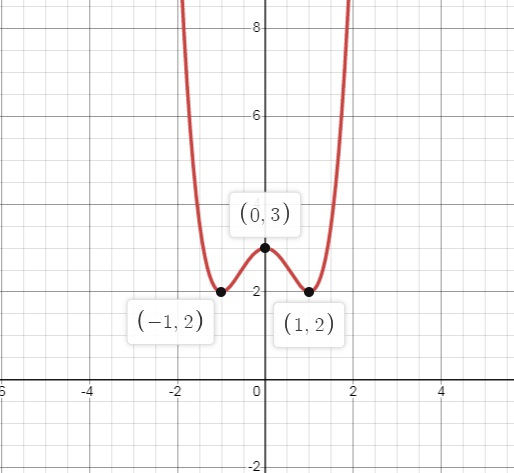
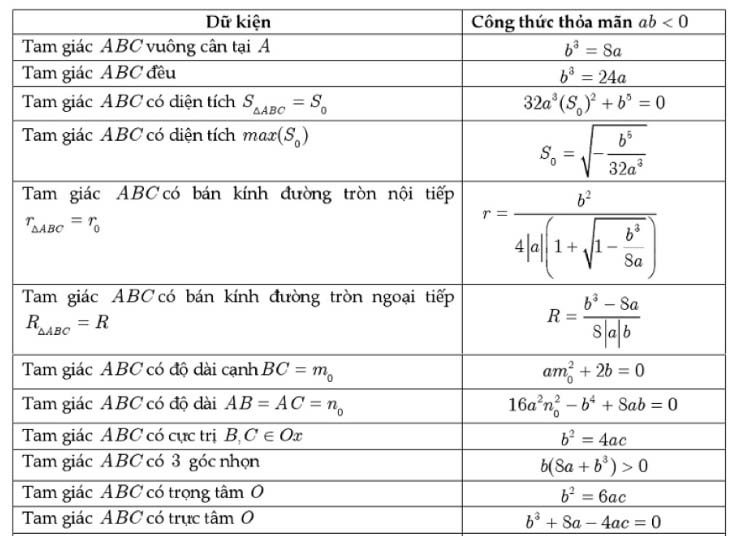
Công thức tính nhanh các bài toán cực trị

Dưới đây là bảng tổng hợp các công thức tính cực trị nhanh của các dạng toán khác nhau để giúp các bạn áp dụng giải bài tập nhanh hơn.

Bài tập vận dụng theo từng dạng

Bài tập 1: Tìm m để đồ thị hàm số f(x) = x^4 - 2(m+1)x^2 + m^2 có cực tiểu, cực đại tạo thành một tam giác vuông.

1. m = 2
2. m = 1
3. m = 0
4. m = -1

Gợi ý lời giải:

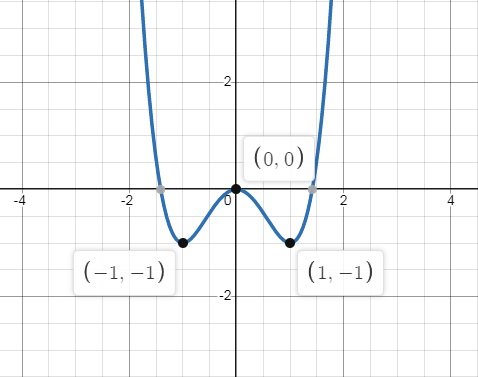
Bài tập 2: Cho hàm số y = x^4 -2mx^2 +2m +m^4. Có bao nhiêu giá trị của m thì đồ thị có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành 1 tam giác có diện tích S = 4?

1. 1
2. 2
3. 3
4. 4

Gợi ý lời giải:

Ta có y’ = 4x^3 -4mx = 0 ⇔ x = 0, g(x) = x^2 - m = 0

Hàm số có 3 cực trị ⇔ y’ = 0 có 3 nghiệm phân biệt ⇔ ∆ > 0 ⇔ m > 0 (*)

Với điều kiện (*), phương trình y’= 0 có 3 nghiệm x1 = -√m, x2 = 0, x3 = √m. Hàm số đạt cực trị tại x1, x2, x3. Gọi A (0; 2m+m^4); B (√m; m^4 - m^2 +2m) là 3 điểm cực trị của đồ thị.

Ta có: AB^2 = AC^2 = m^4 + m; BC^2 = 4m => tam giác ABC cân tại đỉnh A .

Gọi M là trung điểm của BC => M(0; m^4 - m^2 +2m) => AM = m^2.

Vì ABC cân tại A nên AM cũng là đường cao, do đó:

Diện tích tam giác ABC: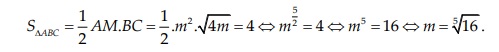

=> Chọn đáp án A.

Bài tập 3:

Cho hàm số y = x^4 - 2mx^2 + m - 1. Có bao nhiêu giá trị của m thì đồ thị có ba điểm cực trị, đồng thời ba điểm cực trị đó lập thành một tam giác có bán kính đường tròn ngoại tiếp bằng 1?

1. 3
2. 1
3. 0
4. 2

Gợi ý lời giải:

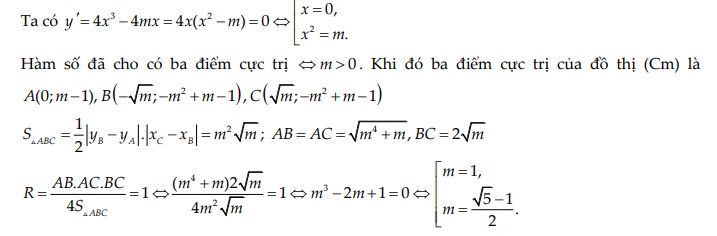
=> Chọn đáp án D.

Kết luận:

Qua bài viết trên, thayphu.net đã giới thiệu đến các bạn học sinh cách tính cực trị hàm trùng phương, điều kiện và công thức tính nhanh. Kèm theo đó là các bài tập vận dụng để các bạn có thể luyện tập thêm. Mong rằng qua bài viết này, các bạn đã nắm rõ các kiến thức để áp dụng thật tốt vào việc giải đề để rút ngắn thời gian giải bài tập. Bởi lẽ, đây là dạng toán nâng cao thường xuyên xuất hiện ở mức 7 đến 8+ trong các đề thi quan trọng.