Công thức tính thể tích khối trụ tròn xoay và bài tập

Khám phá công thức tính khối trụ tròn xoay dễ dàng với công thức πr²h. Tính toán nhanh chóng và chính xác để giải quyết các bài toán liên quan đến hình trụ.

Tính thể tích của một hình trụ là một trong những bài toán cơ bản và quan trọng, đặc biệt trong việc giải quyết các bài toán liên quan đến hình học không gian. Công thức tính thể tích khối trụ tròn xoay rất đơn giản và dễ hiểu, chỉ cần áp dụng công thức và tính toán theo đúng thứ tự. Hãy cùng thayphu tìm hiểu chi tiết về cách tính thể tích hình trụ nhé!

Khối trụ tròn xoay

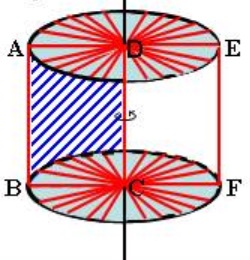
Quan sát hình chữ nhật ABCD, quay hình chữ nhật ABCD một vòng quanh cạnh CD cố định ta được một hình trụ.

Trong đó:

• AB quét trên mặt xung quanh của hình trụ.
• DA, CB quét lên 2 đáy của hình trụ và là các bán kinh của hai mặt đáy.
• AB,EF là các đường sinh.
• Độ dài đường sinh là chiều cao của hình trụ.
• CD là trục của hình trụ.

Công thức tính thể tích khối trụ tròn xoay

Thể tích của hình trụ tròn xoay là giới hạn thể tích của khối lăng trụ đều nội tiếp khối trụ đó khi một số cạnh đáy được tăng lên vô hạn.

Công thức tính thể tích khối trụ tròn xoay là:

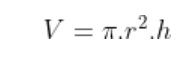
Trong đó:

• V là thể tích của khối hình trụ.
• r là bán kính đáy của khối trụ.
• h là chiều cao của khối trụ.
• Đơn vị tính là m^3.

Các dạng bài tập về thể tích hình trụ tròn xoay

Dạng 1: Các câu hỏi lý thuyết về hình trụ và thể tích khối trụ

Bài 1: Tập hợp các điểm M trong không gian cách đều đường thẳng A cố định một khoảng R không đổi R>0 là :

Lời giải:

Tập hợp các điểm M trong không gian cách đều đường thẳng A cố định một khoảng R không đổi R>0 là một mặt trụ => đáp án D

Bài 2: Cho hai điểm A, B cố định. Tập hợp các điểm M sao cho diện tích tam giác MAB không đổi là

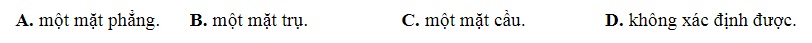
Lời giải

Vì AB cố định nên diện tích tam giác MAB không đổi khi d(M, AB) = const hay M thuộc mặt trụ trục là đường thằng AB song song

=> Ta có hình vẽ :

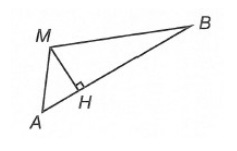
Với công thức:

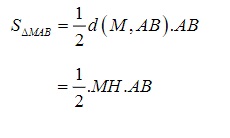
Vậy từ đây ta có thể thấy đây là một mặt trụ

=> Chọn đáp án đúng B

Dạng 2: Tính thể tích của khối trụ khi cho bán kính đáy và chiều cao

Bài 1: Tính theo a thể tích của một khối trụ có bán kính đáy là a, chiều cao bằng 2a

Lời giải:

Cho hình vẽ

Áp dụng công thức tính thể tích ta có:

V = п R^2. h => V= пa^2.2a = 2пa^3

Dạng 3: Tính thể tích khối trụ cho bán kính đáy và chu vi thiết diện

Bài 1: Một hình trụ có bán kính đáy bằng a, chu vi thiết diện qua trục bằng 10a. Tính thể tích của khối trụ đã cho.

Lời giải:

Ta có hình vẽ

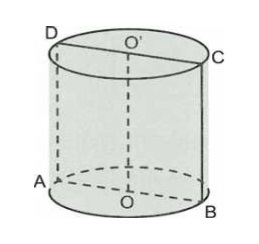
Gọi ABCD là thiết diện qua trục của hình trụ, ta có ABCD là hình chữ nhật. Từ giả thiết suy ra AB = 2a và 2(AB+BC) = 10a => BC=3a

Vậy ta có thể tính thể tích của hình trụ trên là:

V = пa^2 . 3a= 3пa^3

Dạng 4: Tính thể tích khối trụ khi đã cho độ dài đường chéo và và một góc.

Bài 1: Cắt một khối trụ bởi mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có cạnh AB và cạnh CD nằm trên hai đáy của khối trụ. Biết BD= a√2 và 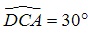. Tính theo a thể tích khối trụ.

Trả lời:

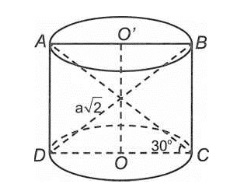
Từ hình vẽ đã cho ta chứng minh được AC=BD = a√2

Xét tam giác ADC vuông tại D ta có

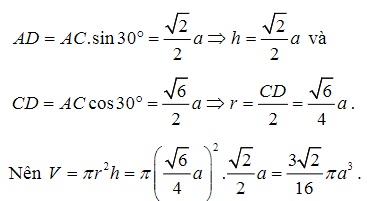
Dạng 5: Cho hình chữ nhật gọi một phần là thể tích khối trụ tạo thành khi có hình chữ nhật quay xung quanh 2 cạnh.

Bài 1: Cho hình chữ nhật ABCD có AD = 3AB. Gọi V1 là thể tích của khối trụ tạo thành khi cho hình chữ nhật quay xung quanh cạnh AB, V2 là thể tích khối trụ tạo thành khi cho hình chữ nhật quay xung quanh cạch AD. Tỷ số V1/V2

Lời giải

Khối trụ tạo thành khi cho hình chữ nhật ABCD quay xung quanh cạnh AB có bán kính đáy và chiều cao lần lượt là:

r1 = AD = 3BA ; h1 = AB

Thể tích của khối trụ này là :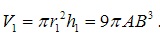

Khối trụ tạo thành khi cho hình chữ nhật ABCD quay xung quanh cạnh AD có bán kính đáy và chiều cao lần lượt là: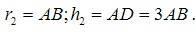

Thể tích của khối trụ này là :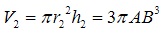

=>

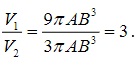
Dạng 6: Tính thể tích khối trụ tròn xoay khi cho hình thang vuông quay quanh miền có cạnh chưa đường thẳng.

Bài 1: Cho hình thang ABCD vuông tại A và B với 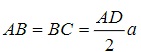. Quay hình thang và miền trong của nó quanh đường thẳng chứa cạnh BC. Thể tích V của khối tròn xoay.

Lời giải:

Cho hình vẽ

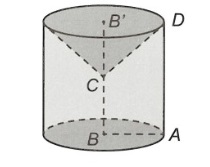
V = V1 - V2 trong đó:

V1 là thể tích khối trụ có bán kính đáy BA = a và chiều cao AD = 2a

V2 là thể tích khối nón có bán kính đáy B’D = a, chiều cao CB’= a

Khi đó ta có: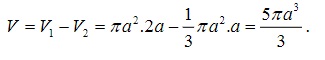

Dạng 7: Cho thể tích tính bán kính của khối trụ

Bài 1: Trong tất cả các khối trụ có cùng thể tích 330, xác định bán kính đáy của khối trụ có diện tích toàn phần nhỏ nhất

Cho hình vẽ

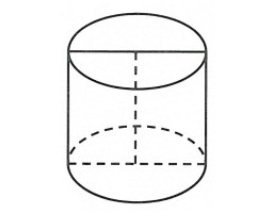
V = 330 => hпR^2 = 330 => h = 330/пR^2

Khi đó diện tích toàn phần khối trụ là

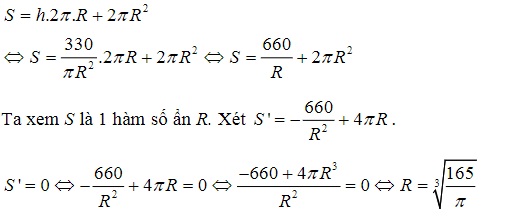
Bài tập tính khối trụ tròn xoay tự luyện tại nhà

Bài tập tự luyện ở nhà không chỉ giúp duy trì trí thông minh mà còn giúp tăng cường sự linh hoạt và sự kiên nhẫn. Tuy nhiên, không phải ai cũng biết cách để tự luyện tại nhà một cách hiệu quả. Dưới đây là một số bài tập tự luyện về công thức tính thể tích khối trụ tròn xoay.

Phần trắc nghiệm

Bài tập tự luận

Câu 1: Một hộp bóng bàn hình trụ có bán kính R, chứa được 10 quả bóng sao cho các quả bóng tiếp xúc với thành hộp theo một đường tròn và tiếp xúc với nhau. Quả trên cùng và quả dưới cùng tiếp xúc với hai nắp hộp. Tính thể tích khối trụ mà thể tích của các quả bóng bàn không chiếm chỗ.

Câu 2: Người ta thả một viên billiards snooker có dạng hình cầu với bán kính nhỏ hơn 4,5 cm vào một chiếc cốc hình trụ đang chứa nước thì viên billiards đó tiếp xúc với đáy cốc và tiếp xúc với mặt nước sau khi dâng (tham khảo hình vẽ bên). Biết rằng bán kính của phần trong đáy cốc bằng 5,4cm và chiều cao của mực nước ban đầu trong cốc bằng 4,5cm. Tính bán kính của viên billiards

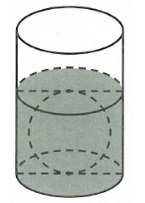
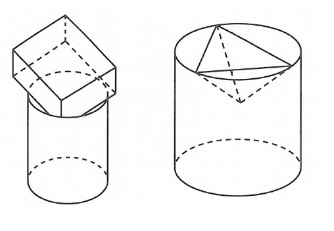
Câu 3: Có một cái bể hình trụ cao 10dm với bán kính đáy 4dm chứa đầy nước bị một thùng gỗ hình lập phương đóng kín rơi vào làm cho một lượng nước V tràn ra. Biết rằng cạnh thùng gỗ là 8dm và khỉ nó rơi vào miệng bể, một đường chéo dài nhất của nó vuông góc với mặt bể, ba cạnh của thùng chạm vào thành của bể như hình vẽ. Tính V

Kết luận

Bài viết trên là những công thức tính thể tích khối trụ tròn xoay và các dạng bài tập liên quan. Hy vọng rằng những thông tin này sẽ giúp cho các em ăn trọn điểm trong dạng toán này. Đừng quên truy cập trang web thayphu.net để có thêm nhiều thông tin khác nhé!