Công thức nguyên hàm lnx, phương pháp giải và bài tập

Nguyên hàm lnx ký hiệu là ∫ ln(x), xem công thức, các phương pháp tính và các dạng bài tập về nguyên hàm lnx trong chương trình Toán giải tích 12.

Bài viết này, thayphu sẽ giới thiệu đến các bạn công thức nguyên hàm lnx, đây được coi là một công thức quan trọng trong Toán Giải tích 12. Chúng ta sẽ cùng tìm hiểu định nghĩa, các công thức giúp chúng ta tính nguyên hàm của hàm số tự nhiên logarit cơ số e của nguyên hàm lnx và cách áp dụng chúng vào các dạng bài tập khác nhau.

Qua đó, hãy cùng thayphu tìm hiểu rõ hơn về công thức nguyên hàm lnx và các dạng bài sẽ xuất hiện trong đề thi THPT QG trong bài viết bên dưới.

Công thức nguyên hàm lnx là gì?

Để hiểu rõ hơn về công thức này, chúng ta cần biết rằng nguyên hàm của một hàm số f(x) là một hàm số F(x) mà đạo hàm của nó bằng hàm số f(x). Nguyên hàm của 1 hàm số f(x) thường được ký hiệu là ∫ ln(x).

Và trong trường hợp của hàm số ln(x), ta cần tìm một hàm số F(x) sao cho F'(x)=ln(x)dx. Hay nói các khác là:

∫ ln(x)dx = F(x) + C

Và ta có cách tính của nguyên hàm lnx là:

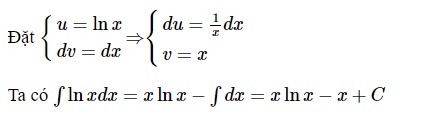
Bảng công thức nguyên hàm sơ cấp và mở rộng

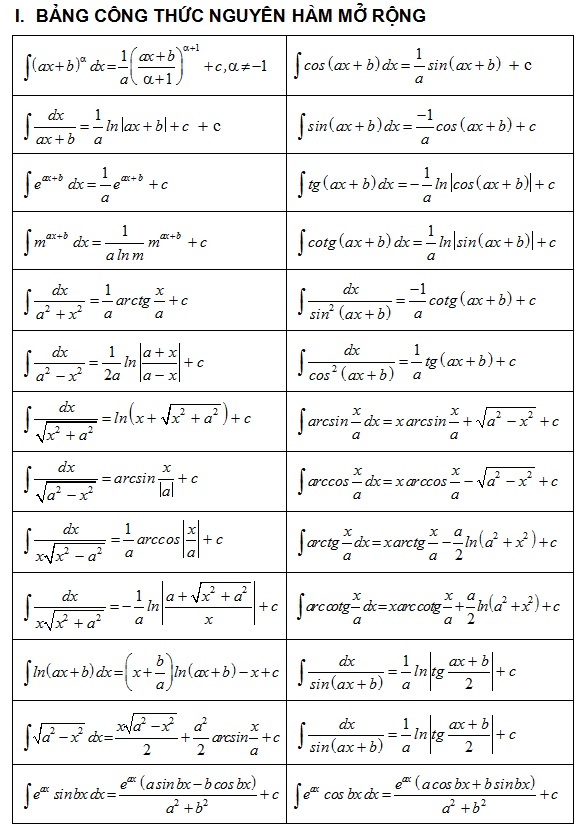
Ta có bảng công thức tính nguyên hàm của hàm số sơ cấp và một số dạng khác thường gặp như sau:

Ngoài ra, ta còn có thêm 1 bảng về các dạng mở rộng và nâng cao hơn của của các công thức nguyên hàm:

Cách tính nguyên hàm lnx chuẩn nhất

• Cách 1: Sử dụng quy tắc tính nguyên hàm:

Theo quy tắc tính nguyên hàm, nguyên hàm của ln(x) là x * ln(x) - x + C, trong đó C là hằng số thuộc R.

• Cách 2: Sử dụng phép tích phân:

Tích phân của lnx có thể tính bằng cách áp dụng phép tích phân không xác định như sau:

∫ ln(x) dx = x * ln(x) - ∫ x/x dx

Để tính ∫ x/x dx, chúng ta có thể đơn giản hóa bằng cách loại bỏ x/x:

∫ x/x dx = ∫ 1 dx

Suy ra, ta có:

∫ ln(x) dx = x * ln(x) - ∫ 1 dx

∫ ln(x) dx = x * ln(x) - x + C

Các dạng bài tập vận dụng của nguyên hàm lnx

• Dạng 1: Nguyên hàm ln(x) cơ bản

Bài tập 1: Tìm nguyên hàm của hàm số sau: ∫ x.lnx.dx

Gợi ý lời giải:

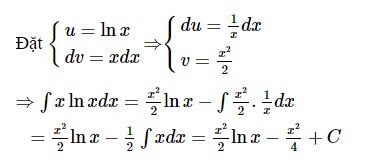
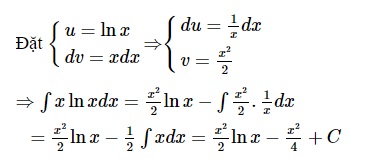
Bài tập 2: Với 12 ∫ln(x + 1)dx = aln3 + bln2 + c, trong đó a, b, c là các số nguyên. Tính S = a + b = c

Gợi ý lời giải:

Đặt u = ln(x + 1), dv = dx

=> du = 1/ (x + 1) dx, v = x + 1

Lúc này ta có:

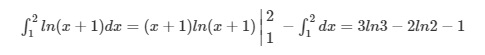
Vậy ta có: a=3, b=-2, c=-1.

Từ đó suy ra => a+b+c=0

Bài tập 3: ∫ 2x.lnx(x - 1)dx

Gợi ý lời giải:

Đặt u= ln(x - 1), dv = 2x.dx

=> du = 1/(x - 1)dx, v =x2 - 1

Ta có: ∫ 2x.lnx(x - 1)dx

⇔ (x2 -1)ln(x -1) - ∫ (x + 1)

⇔ (x2 -1)ln(x -1) - ∫ (x + 1)

⇔ (x2 -1)ln(x -1) - (x2/2) - x + C

Đặt u = ln(1 +x), dv = (1/x2)dt

=>du= 1/(1+ x)dx, v = -1/x -1 = -(1+ x)/x

Từ đó suy ra: F(x) = -(1+ x)/x. ln(1 +x) + ∫(1/x)dx

= -(1+ x)/x. ln(1 +x) +lnx + C

Kết luận

Như vậy, bài viết trên thayphu.net đã giới thiệu chi tiết cho các bạn học sinh về khái niệm và công thức của nguyên hàm lnx. Công thức này sẽ giúp chúng ta tính toán giá trị nguyên hàm của hàm số này và áp dụng vào các bài toán tính toán phức tạp trong giải tích tích phân.

Các bạn học sinh cần nắm rõ khái niệm cơ bản này để có thể hiểu rõ các dạng toán nâng cao hơn. Đồng thời, việc hiểu và áp dụng công thức nguyên hàm của ln(x) là rất quan trọng trong nhiều lĩnh vực toán học và khoa học khác nhau.