Tổng hợp công thức Logarit lớp 12 đầy đủ nhất

Bảng công thức Logarit lớp 12 đầy đủ nhất, tìm hiểu định nghĩa, các tính chất Logarit sẽ giúp các bạn dễ dàng làm quen và giải các bài tập khó.

Trong chương trình lớp 12 chúng ta sẽ được học những công thức Logarit nào? Có những công thức sẽ suy ra từ công thức khác. Chính vì vậy mà ghi nhớ những công thức tổng quát đóng vai trò hết sức quan trọng. Hãy đọc bài viết dưới đây của thayphu.net để biết thêm về công thức này nhé.

Định nghĩa Logarit là gì?

Định nghĩa Logarit

Logarit là một phép toán số học liên quan đến quan hệ giữa các lũy thừa của một số cơ sở và các số mũ của nó. Cụ thể, logarit của một số x với cơ số a là số mũ mà a cần được lấy để được x, được ký hiệu là logₐ x. Nói cách khác, nếu aᵏ = x, thì logₐ x = k.

Ví dụ: log₃ 9 bằng 2, bởi vì 3² = 9. Tương tự, log₁₀ 100 bằng 2, bởi vì 10² = 100.

Logarit có ứng dụng rộng rãi trong toán học, khoa học, kỹ thuật và các lĩnh vực khác để giải quyết các bài toán liên quan đến số học và các dữ liệu số lớn.

Logarit thập phân và logarit tự nhiên

Logarit thập phân và logarit tự nhiên

Logarit thập phân

Logarit thập phân (hay còn gọi là logarit cơ số 10) của một số thực dương x được định nghĩa là số mà khi đưa 10 lên một lũy thừa bằng với số đó sẽ cho kết quả là x. Ký hiệu của logarithm thập phân là log(x) hoặc có thể viết là lg(x).

Cụ thể, nếu log(x) = y thì có nghĩa là 10^y = x. Ví dụ, log(100) = 2 vì 10^2 = 100.

Logarithm thập phân được sử dụng rất phổ biến trong các bài toán toán học, khoa học tự nhiên, kỹ thuật, công nghệ thông tin và các lĩnh vực khác. Nó là một trong những công cụ cơ bản giúp giải quyết các bài toán liên quan đến phép tính mũ và phép tính lũy thừa.

Logarit tự nhiên

Logarit tự nhiên (hay còn gọi là logarit cơ số e) của một số thực dương x được định nghĩa là số mà khi đưa số e lên một lũy thừa bằng với số đó sẽ cho kết quả là x. Ký hiệu của logarithm tự nhiên là ln(x).

Cụ thể, nếu ln(x) = y thì có nghĩa là e^y = x. Ví dụ, ln(e) = 1 vì e^1 = e.

Logarit tự nhiên cũng rất phổ biến trong các bài toán toán học, khoa học tự nhiên, kỹ thuật, công nghệ thông tin và các lĩnh vực khác. Nó có liên quan mật thiết đến số e, một hằng số toán học rất quan trọng và có xu hướng xuất hiện trong các vấn đề liên quan đến tốc độ tăng trưởng, vi phân và tích phân.

Tính chất của logarit mà bạn cần biết

Dưới đây là các tính chất quan trọng của logarit:

1. Tính chất của phép cộng: log(a*b) = log(a) + log(b).

Điều này có nghĩa là logarit của tích của hai số bằng tổng của logarit của từng số đó.

2. Tính chất của phép trừ: log(a/b) = log(a) - log(b).

Điều này có nghĩa là logarit của thương của hai số bằng hiệu của logarit của từng số đó.

3. Tính chất của phép mũ: log(a^b) = b*log(a).

Điều này có nghĩa là logarit của số mũ bằng tích của logarit của số gốc và số mũ đó.

4. Tính chất của phép đổi cơ số: log(b,a) = log(c,a) / log(c,b).

Điều này có nghĩa là logarit của a theo cơ số b bằng logarit của a theo cơ số c chia cho logarithm của b theo cơ số c.

5. Tính chất của logarit của một: log(a) = 0.

Điều này có nghĩa là logarit của số một bất kỳ luôn bằng không.

6. Tính chất của logarit của cơ số: log(a,a) = 1.

Điều này có nghĩa là logarit của một số bất kỳ theo cùng một cơ số bất kỳ luôn bằng một.

7. Tính chất của phép đổi dấu: log(a) = -log(1/a).

Điều này có nghĩa là logarit của một số bằng âm logarithm của nghịch đảo của số đó.

Tổng hợp các công thức Logarit

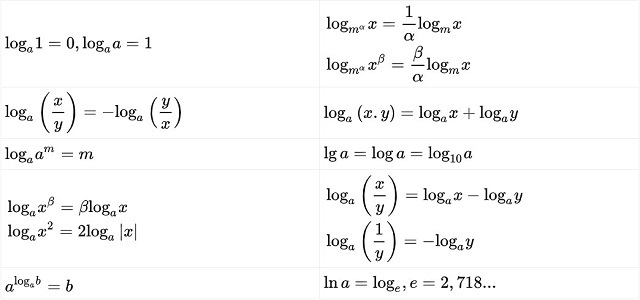
Bảng tổng hợp các công thức Logarit (x,y >0)

Công thức đạo hàm của Logarit cần nhớ

Công thức đạo hàm của Logarit cần nhớ

Công thức Logarit Nepe

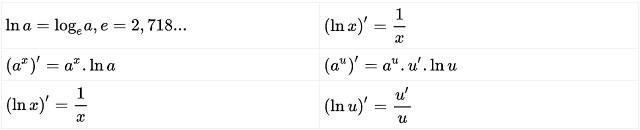
Các công thức Logarit Nepe

Các công thức mũ Logarit không nên bỏ qua

Các công thức mũ Logarit không nên bỏ qua

Làm cách nào để ghi nhớ công thức Logarit

Để nhớ công thức Logarit lớp 12 hiệu quả, bạn có thể áp dụng các phương pháp như sau:

• Hiểu rõ ý nghĩa của các công thức, đặc biệt là các tính chất của logarit. Khi bạn hiểu được ý nghĩa của mỗi công thức, bạn sẽ dễ dàng nhớ chúng hơn.

• Tập trung vào các tính chất chính của logarit, bao gồm tính chất của phép cộng, phép trừ, phép mũ, phép đổi cơ số, logarithm của một và logarithm của cơ số.

• Luyện tập tính toán logarit bằng cách giải các bài tập về logarit. Khi bạn thực hành tính toán logarit nhiều lần, các công thức sẽ dần được ghi nhớ trong bộ não của bạn.

• Tạo ra các câu hỏi và trả lời chúng về các công thức logarit. Bạn có thể sử dụng các flashcard để viết các công thức và đặt câu hỏi cho mình, sau đó giải đáp câu hỏi đó.

Bài tập áp dụng

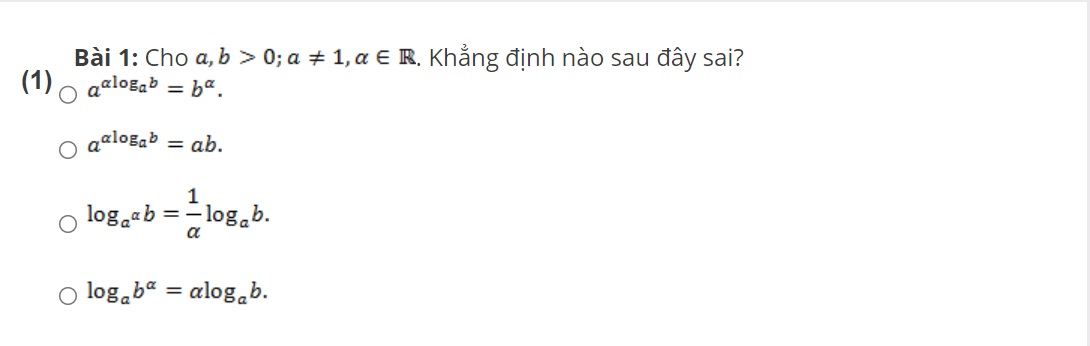
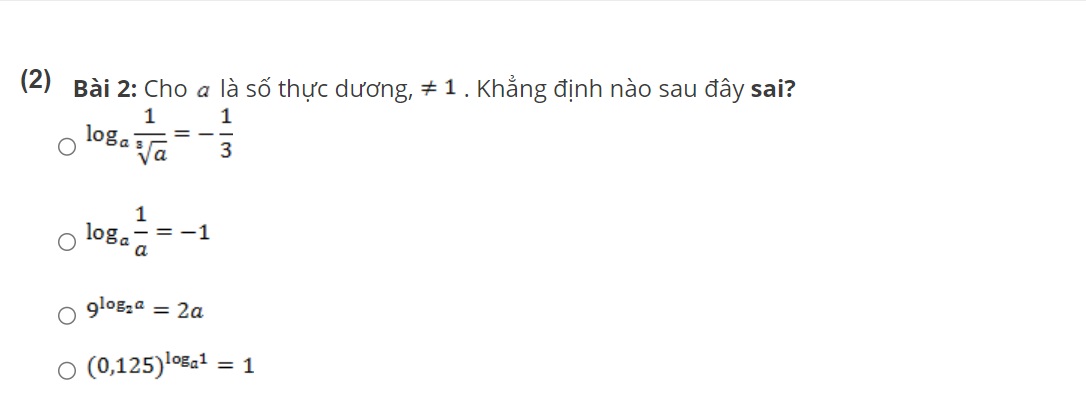
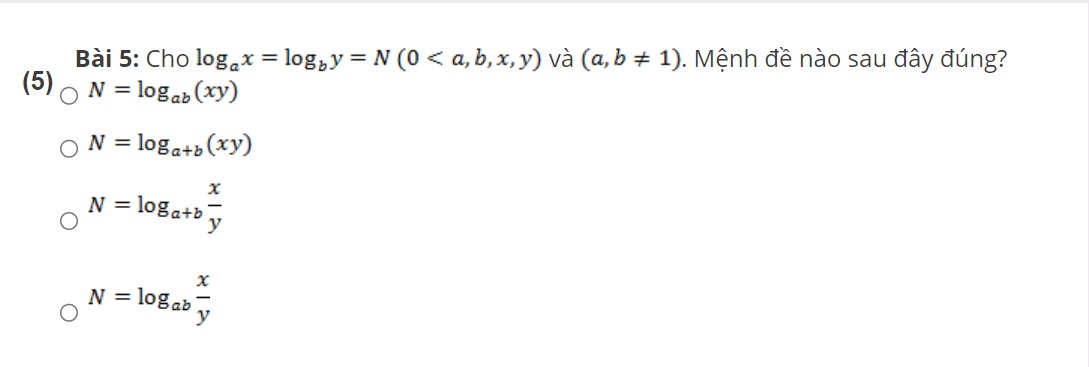
Như vậy bài viết trên đây đã tổng hợp các công thức Logarit cho tất cả các bạn đọc. Đây đều là những công thức cơ bản nên nếu các bạn muốn có điểm cao trong tất cả các bài kiểm tra thì đừng quên lưu lại những công thức này nhé.