Công thức và cách tính thể tích hình trụ đơn giản dễ hiểu

Cách tính thể tích hình trụ là công thức tính toán đơn giản dễ áp dụng. Giúp tính toán khối lượng của một vật thể trụ, hữu ích trong nhiều lĩnh vực khác nhau.

Hình trụ là một trong những hình học cơ bản và được sử dụng rộng rãi trong toán học, khoa học và kỹ thuật. Nếu bạn đang tìm cách tính thể tích hình trụ để có thể dành được điểm cao hơn. Hãy theo dõi bài viết này của thayphu để có được giải pháp đơn giản và hiệu quả.

Khái niệm về hình trụ

Hình trụ được thấy nhiều trong đời sống

Hình trụ

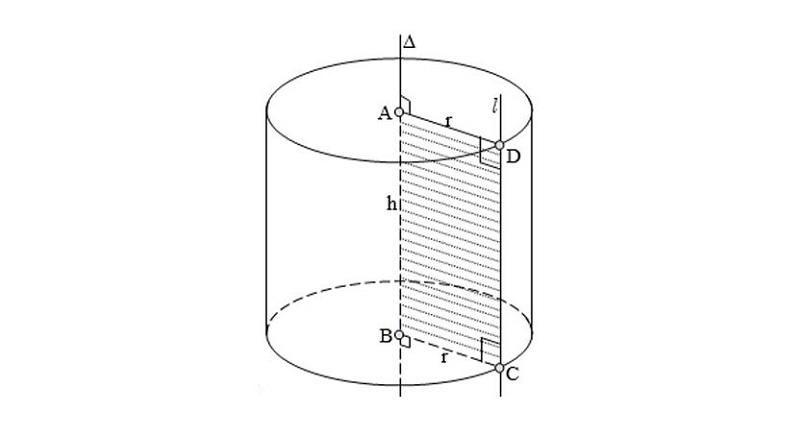
Hình trụ là một hình học ba chiều được tạo thành từ một đáy hình tròn và một mặt trụ thẳng đứng. Hình trụ có hai đặc điểm quan trọng là đường bao quanh (viền) và thể tích.

Đường bao quanh của hình trụ được tính bằng cách cộng độ dài của chu vi đáy và chu vi của mặt trụ. Thể tích của hình trụ được tính bằng cách nhân diện tích đáy với chiều cao của hình trụ.

Hình trụ được sử dụng rộng rãi trong các lĩnh vực kỹ thuật, xây dựng, cơ khí và toán học.

Ví dụ: lon nước ngọt, bình xịt côn trùng, chai sữa,...

Cắt hình trụ bởi một mặt phẳng

Khi cắt hình trụ bởi một mặt phẳng song song với đáy thì mặt cắt là một hình tròn đáy.

Khi cắt hình trụ bởi một mặt phẳng song song với trục thì mặt cắt là một hình chữ nhật.

Công thức tính diện tích hình trụ

Công thức tính diện tích là một phần để biết được cách tính thể tích hình trụ vậy nên, để tính diện tích xung quanh (hay còn gọi là diện tích bên) của một hình trụ, ta sử dụng công thức: Sxq = 2πrh

Trong đó:

• Sxq là diện tích xung quanh của hình trụ
• r là bán kính đáy của hình trụ
• h là chiều cao của hình trụ
• π là số pi, có giá trị xấp xỉ 3.14

Để tính diện tích toàn phần của một hình trụ, ta sử dụng công thức: Stp = Sđ + Sxq

Trong đó:

• Stp là diện tích toàn phần của hình trụ
• Sđ là diện tích đáy của hình trụ, có giá trị là πr^2
• Sxq là diện tích xung quanh của hình trụ, có giá trị là 2πrh

Vậy công thức tính diện tích toàn phần của hình trụ là: Stp = πr^2 + 2πrh

Cách tính thể tích hình trụ

Cách tính thể tích hình trụ khá là đơn giản và dễ dàng áp dụng vào các bài tập. Vậy nên các bạn cần phải học thuộc những công thức trọng tâm để từ đó có thể suy ra và tính được những kết quả khác.

Công thức tính thể tích hình trụ

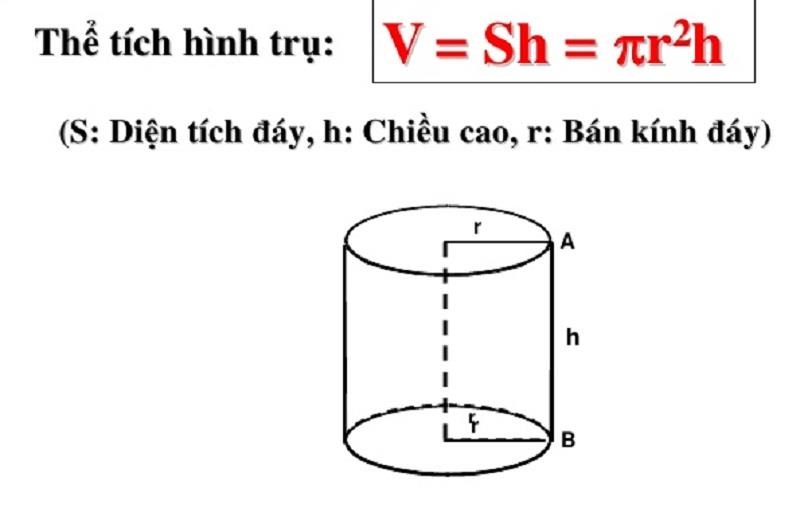
Cách thể tích hình trụ, ta cần biết độ dài của đường kính đáy và chiều cao của nó vậy nên công thức tính thể tích của hình trụ là: V = πr^2h

Trong đó:

• V là thể tích của hình trụ
• π là số pi, có giá trị xấp xỉ 3.14
• r là bán kính của đáy hình trụ
• h là chiều cao của hình trụ

Các bước tính thể tích hình trụ

Các bước tính thể tích đơn giản bạn có thể tính toán thể tích của hình trụ một cách nhanh chóng và chính xác. Để tính thể tích của một hình trụ, bạn có thể làm theo các bước sau:

• Xác định bán kính (r) của đáy hình trụ. Bán kính là khoảng cách từ tâm của đáy đến bất kỳ điểm nào trên đường viền của đáy.
• Xác định chiều cao (h) của hình trụ. Chiều cao là khoảng cách từ đáy của hình trụ đến đỉnh của nó.
• Sử dụng công thức tính diện tích hình tròn để tính diện tích (A) của đáy hình trụ: A = πr^2.
• Sử dụng công thức tính thể tích hình trụ để tính thể tích (V) của nó: V = A x h = πr^2 x h.
• Đơn vị của thể tích sẽ phụ thuộc vào đơn vị được sử dụng cho bán kính và chiều cao. Nếu bán kính được đo bằng mét và chiều cao được đo bằng mét, thì thể tích sẽ được tính bằng mét khối (m^3).

Ví dụ 1: Một hình trụ có bán kính đáy r = 5 cm, chiều cao h = 7cm. Tính thể tích của hình trụ

Trả lời:

Áp dụng công thức : V = πr^2h

=> V = π5^2. 7 ⇔ V= 350π

Ví dụ 2:

a) Tính chiều cao của hình trụ (T) có diện tích toàn phần là 120π (cm2) và bán kính đáy bằng 6 cm.

b) Tính độ dài đường sinh của hình trụ (T) có thể tích là 81π (cm3) và đường kính đáy gấp ba lần đường kính của đường sinh.

Trả lời:

a) Áp dụng công thức diện tích toàn phần ta có: Stp = 2πrh + 2πr^2 = 2π.6.h + 2π.6^2 = 120π ⇒ h = 4(cm)

=> chiều cao của hình trụ là 4 cm.

b) Gọi bán kính đáy của hình trụ là r

Ta có đường sinh gấp 3 lần đường đáy => ta có h= 3r

Dựa vào số liệu đã cho t có công thức sau: V = πr^22 h = πr^2.3r = 81π ⇒ r = 3

=> đường sinh = 3.3 = 9 cm.

Kết luận

Bài viết trên đây là cách tính thể tích hình trụ đơn giản và dễ hiểu. Thể tích của một hình trụ là một phép tính cơ bản trong toán học và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau. Vậy nên các em học sinh cần phải nắm chắc kiến thức để làm nền tảng sau này. Hãy truy cập trang web thayphu.net để có thể học thuộc các công thức hình học nhé!