Bảng nguyên hàm đầy đủ, cách ghi nhớ và bài tập áp dụng

Nguyên hàm là kiến thức xuất hiện trong đề thi toán Trung học phổ thông Quốc gia. Việc ghi nhớ bảng nguyên hàm đầy đủ, chính xác là vô cùng quan trọng.

Nguyên hàm là một bài toán không chỉ xuất hiện trong các bài kiểm tra đại số lớp 12 mà còn là một phần của đề thi đại học, cao đẳng. Đây là một dạng toán khó với rất nhiều công thức cần phải ghi nhớ và học thuộc. Và nếu không nắm được những kiến thức này, chắc chắn người học không thể giải quyết bài toán nào liên quan đến cả nguyên hàm và tích phân.

Chính vì vậy, thayphu đã tổng hợp công thức bảng nguyên hàm đầy đủ, chi tiết hỗ trợ các em khi học toán 12 một cách hiệu quả hơn.

Giới thiệu về nguyên hàm

Nguyên hàm là một kiến thức hay nhưng cũng làm khó rất nhiều học sinh trong quá trình học tập

Trước khi có thể nắm và ghi nhớ bảng nguyên hàm một cách đầy đủ, các em cần ghi nhớ khái niệm về nguyên hàm. Theo đó, khái niệm nguyên hàm được định nghĩa như sau: Cho hàm số trên f(x) xác định trên K (K có thể là một khoảng, đoạn hoặc nửa khoảng trên tập hợp R).

Lúc này, hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu thoả mãn điều kiện F’(x)= f(x) với mọi x thuộc K. Lưu ý, với mọi hàm số liên tục trên K (với K thuộc tập hợp R) đều có nguyên hàm K.

Ký hiệu nguyên hàm: Nếu y = F(x) là một nguyên hàm của hàm số y= f’(x) thì f(x)dx = F(x) +C, C ∊ R.

Tổng hợp bảng công thức nguyên hàm đầy đủ và chi tiết

Như đã đề cập ở trên, nguyên hàm là một trong những dạng toán rất khó trong chương trình toán lớp 12. Bởi chỉ khi các em học tốt nguyên hàm thì mới có thể học tốt kiến thức toán khác là tích phân. Vậy làm thế nào để có thể ghi nhớ những công thức nguyên hàm rắc rối và phức tạp kia? Thayphu đã phân loại công thức của những nguyên hàm thường gặp bao gồm 3 nhóm là công thức nguyên hàm cơ bản, mở rộng và đặc biệt.

Bảng nguyên hàm đầy đủ dạng cơ bản

Mỗi loại nguyên hàm đều sẽ có những công thức riêng, tuy nhiên, để nhớ được công thức của hai dạng trên, các em bắt buộc phải nhớ bảng nguyên hàm cơ bản. Bởi nó chính là bảng công thức nền tảng, bao gồm 13 công thức.

Ví dụ minh hoạ: 4 xdx = 4 + C

Bảng nguyên hàm đầy đủ dạng mở rộng

Nguyên hàm mở rộng còn được biết đến là bảng nguyên hàm của các hàm số hợp, ta có bảng nguyên hàm đầy đủ dạng mở rộng như sau.

Ví dụ minh hoạ: (x5-3x) dx = x56 - 3x22 + C

Bảng công thức nguyên hàm dạng đặc biệt ( điều kiện a khác 0)

Bảng công thức nguyên hàm đặc biệt (nâng cao) rất khó để ghi nhớ. Những công thức nâng cao này thường là câu để phân biệt chất lượng học sinh, được áp dụng để giải các bài toán nguyên hàm phức tạp. Vậy nên, không nên học vẹt, học tủ mà nên sử dụng các phương pháp phân tích logic để việc học thuộc trở nên dễ dàng hơn nhé.

Những lưu ý khi học bảng nguyên hàm tốt nhất

Bảng nguyên hàm đầy đủ sẽ là công cụ hỗ trợ các em học sinh trong việc ghi nhớ công thức nguyên hàm một cách tốt hơn. Tuy nhiên, để nắm được bản chất thực sự của các công thức trong bảng nguyên hàm, các em cần lưu ý những điều sau:

Các em cần phải có kiến thức cơ bản về đạo hàm và vi phân (bởi các bài toán vi phân và đạo hàm có liên quan đến nhau). Đồng thời, cần phải phân biệt được một số công thức đạo hàm của hàm sơ cấp và hàm hợp.

Nắm được chính xác các tính chất của một nguyên hàm đầy đủ, bao gồm.

• Nếu f(x) là hàm số có nguyên hàm thì (f(x)dx)’= f(x); d(f(x)dx) = f(x)dx.
• Nếu F(x) có đạo hàm thì d((F(x)) = F(x) +C, C thuộc tập R.
• Phép cộng, phép trừ: f[f(x) ± g(x)]dx= f(x)dx ± g(x)dx, điều kiện hàm f và hàm g liên tục trên K.
• Phép nhân đạo hàm với một hằng số thực khác 0: k.f(x)dx = k.f(x)dx với mọi k khác 0.

Đối với bài toán nguyên hàm không chỉ dừng lại ở nguyên hàm của một số mà còn liên quan đến hàm lượng giác. Ví dụ, bên cạnh công thức nguyên hàm dx = x + C, ta có công thức lượng giác là cosxdx = sinx +C. Chính vì vậy, khi học bảng nguyên hàm đầy đủ, các em nên tránh nhầm lẫn công thức nguyên hàm của các hàm lượng giác.

Những công thức nguyên hàm đặc biệt có thể được chứng minh bằng cách lấy đạo hàm vế trái, hoặc tính bằng cách đổi biến số để đưa chúng về hàm cơ bản. Đặt u = ax +b, suy ra du= A.dx, suy ra dx = B.du.

Mẹo ghi nhớ bảng nguyên hàm đầy đủ, chính xác

Một số mẹo hay để ghi nhớ bảng nguyên hàm tốt hơn

Bảng nguyên hàm có rất nhiều công thức từ cơ bản đến nâng cao khiến quá trình ghi nhớ của các em học sinh gặp khó khăn, điều này ảnh hưởng đến quá trình học tập và kiểm tra của các em. Do vậy, những mẹo ghi nhớ dưới đây sẽ giúp các em học bảng nguyên hàm cực nhanh và hiệu quả.

• Nhớ bảng nguyên hàm đầy đủ theo quy trình từ công thức cơ bản đến nâng cao. Điều này sẽ giúp các em nhớ vững kiến thức nền tảng, sau đó, phát triển đến kiến thức nâng cao và các công thức đặc biệt hơn, việc giải toán dễ hơn.
• Các em có thể ghi công thức vào giấy nhớ để dán ở những nơi dễ nhìn, dễ học như phòng học, cửa ra vào, cửa tủ lạnh, … Hoặc có thể đặt ghi chú, nhớ nhở trong điện thoại của mình. Sau mỗi ngày học thuộc, các em nên ôn lại kiến thức để chúng in sâu trong não và nhớ lâu hơn.
• Một trong những mẹo giúp ghi nhớ bảng nguyên hàm hiệu quả nữa mà các em có thể áp dụng đó chính là làm thật nhiều và thật đa dạng các loại bài tập. Hãy bắt đầu luyện tập bằng những bài toán trong sgk, và dần dần lên những bài toán trong sách bài tập, trên internet. Các em sẽ làm từ những bài cơ bản đến nâng cao, điều này sẽ giúp các em khi gặp những bài tương tự sẽ dễ dàng tìm được kết quả chính xác.
• Một mẹo để ghi nhớ những công thức nguyên hàm mở rộng đó chính là đặt u(x) = ax+b, ta sẽ được dạng nguyên hàm cơ bản, tuy nhiên có sự khác nhau về hệ số.

Ví dụ: Công thức của nguyên hàm cơ bản xn dx = (x )n+1n+1 + C, nguyên hàm nâng cao (ax+b)n dx = 1a (ax + b)n+1n+1 + C, n∊ R\ {-1}. Để nhớ nguyên hàm này, ta nâng số mũ thành n+1 và chia cho chính số mũ đó. Điểm khác biệt giữa công thức cơ bản và công thức nâng cao là thay x= ax+b và đặt 1a nhân ra ngoài. Ví dụ: x100 dx = (x )100+1100+1 + C= x101101 + C

• Ngoài ra, các em có thể hỏi lắng nghe thầy cô giảng bài trên lớn hoặc hỏi thêm bạn bè ở những phần công thức chưa hiểu để quá trình ghi nhớ dễ dàng hơn.

Những dạng bài tập liên quan đến bảng nguyên hàm đầy đủ, chuẩn xác nhất

Một số bài tập liên quan đến nguyên hàm

Đối với nguyên hàm, chúng ta có rất nhiều dạng toán liên quan đến bảng nguyên hàm vừa được tổng hợp đầy đủ ở trên. Các dạng toán đó bao gồm:

Dạng 1: Tìm nguyên hàm với các phép biến đổi cơ bản

Đây được xem là dạng dễ nhất, dạng cơ bản mà tất cả các học sinh đều phải làm được.

Phương pháp:

• Thực hiện biến đổi hàm số dưới dấu nguyên hàm về dạng tổng/ hiệu của biểu thức chứa x, mỗi biểu thức chứa x được khai triển phải là dạng cơ bản có trong bảng nguyên hàm đầy đủ.

• Sau đó, học sinh áp dụng các công thức được cung cấp trong bảng nguyên hàm cơ bản để thực hiện tính toán.

Bài tập ứng dụng: Tìm nguyên hàm

1. f(x) = x100 - 3x + 1x

2. f(x) = 2x + 5x

3. f(x) = sin4xxcosx

4. f(x) = (5x+3)5

Giải

1. f(x) dx =(x100 - 3x + 1x) dx = x101101 - 3x22 + C

2. f(x) dx = (2x + 5x)dx = 2xln2 + 5xln2 + C

3. f(x) dx =(sin4xcosx )dx = (sin4xx)d(sinx) = sin5x5 + C

4. f(x) dx =((5x+3)5)dx = (5x+3)630 + C

Dạng 2: Phương pháp đặt biến

Phương pháp đặt biến thực chất là phương pháp đưa biến phức tạp thành dạng cơ bản dựa vào bảng nguyên hàm đầy đủ mở rộng.

Phương pháp: Cho f(u) du = F(u) +C và u = u(x) là các hàm số có đạo hàm liên tục, ta được f(u (x))u'(x) dx = F(u (x) +C .

• Đặt u = u(x), từ đó suy ra du=u’(x)dx

• Chuyển hàm tìm được ban đầu sang ẩn u, ta được f(u) du = F(u) +C. Trong đó, F(u) là nguyên hàm của hàm f(u).

• Trả về biến x ban đầu và ta có hàm cần tìm I= F(u(x)) +C. Lưu ý, trong bài toán có thể yêu cầu học sinh tính toán thêm dựa vào bài toán nguyên mẫu này, có thể xem ví dụ dưới đây.

Bài tập ứng dụng: Tìm nguyên hàm I = x+1(x2+2x)2 dx biết x =1

Giải

Ta có: I = x+1(x2+2x)2 dx = 12 2x+2(x2+2x)2 dx = 12 1(x2+2x)2 d(x2+2x)

Đặt u= x2+2x, ta có I = 12 1(u)2 d(u2)= -12u + C. Suy ra, I = -12(x2+2x) + C.

Thay x=1, ta có I = -12(12+2.1)= -16

Dạng 3: Tìm nguyên hàm theo phương pháp từng phần

Dạng toán này khá khó và cần được luyện tập nhiều để có thể nhớ cách làm.

Phương pháp: Với u =u(x), v= v(x) là các hàm số có đạo hàm trên K, ta có, (u.v)’ = u’v. v’u và được viết dưới dạng vi phân là d(uv)= vdu + udv

Khi đó, lấy nguyên hàm hai vế, ta được: d(uv) = v du + u dv.

Suy ra Công thức nguyên hàm từng phần: udv = uv - vdu

Dấu hiệu nhận biết: Hai hàm u(x) và v(x) có tính chất khác nhau, cụ thể:

• u(x) là hàm đa thức, v(x) là hàm lượng giác

• u(x) là hàm đa thức, v(x) là hàm mũ

• u(x) là hàm logarit, v(x) là hàm đa thức

• u(x) là hàm mũ, v(x) là hàm lượng giác

Phương pháp nguyên hàm từng phần: Phương pháp này được thực hiện theo 2 bước chính như sau:

• Bước 1: Đặt u = u(x) suy ra du = u’(x) dx

và đặt dv = v (x)dx suy ra v = v (x)dx

• Bước 2: Áp dụng công thức nguyên hàm từng phần, ta được

udv = uv - vdu

Lưu ý khi đặt u = u(x). Nếu trong bài toán xuất hiện các hàm logarit, đa thức, lượng giác, hàm mũ, thì ta thực hiện theo thứ tự ưu tiên như sau: Nhất lốc - Nhì đa - Tam lượng - Tứ mũ. Câu này được hiểu là ưu tiên đặt u là hàm logarit trước, sau đó mới đến hàm đa thức, lượng giác, hàm mũ.

Khi nguyên hàm v = v (x)dx, dựa vào từng bài toán ta sẽ chọn hằng số thích hợp.

Bài tập ứng dụng: Tìm nguyên hàm của hàm I = ln(sinx + 2 cosx)cos2x dx

Giải

Đặt u = ln(sin x + 2cos x), suy ra du = cosx -2 sinxsin x + 2 cos xdx

Đặt dv = dxcos2x, suy ra v = tan x + 2 = sinx + 2 cosxcosx

Khi đó: I = (tan x + 2)ln(sin x + 2 cos x) - cosx -2 sinxcos x dx

= (tan x + 2)ln(sin x + 2 cos x) - x - 2ln |cos x| + C

Dạng 4: Các bài toán thực tế từ bảng nguyên hàm

Dựa vào bảng nguyên hàm để xác định vận tốc tên lửa trong một khoảng thời gian nhất định

Thông thường, bảng nguyên hàm trong toán học được ứng dụng rất nhiều vào bài toán chuyển động trong môn lý. Cụ thể như sau:

• Một chất điểm chuyển động với phương trình S = S(t), S (t) là quãng đường đi được trong thời gian t, kể từ khi bắt đầu, tức từ lúc t0
• Gọi v(t) là vận tốc tức thời và a(t) là gia tốc tức thời của chất điểm ở thời điểm t. Khi đó ta có v(t) = S’(t) và a(t) = v’(t).
• Suy ra S(t) = v (t)dt và v(t) = a (t)dt

Bài tập ứng dụng: Các nhà khoa học thử nghiệm một loại tên lửa và cho nó bắn từ mặt đất với vận tốc ban đầu bằng 10m/s. Giả sử tên lửa chỉ chị tác động của trọng lực thì sau 5s, vận tốc tối đa đạt được của tên lửa là bao nhiêu?

Giải

Tại thời điểm t0=0, và vận tốc ban đầu là v(0) = 10, quãng đường đi đường ban đầu là s(0) = 0.

Tên lửa chỉ chịu tác động của trọng lực và có chuyển động thẳng đứng nên gia tốc trọng trường tại thời điểm t là s (t) = -9.8 m/s2

Vì nguyên hàm của gia tốc là vận tốc, ta có v(t) = (-9,8)dt = -9,8 t + C1

Do V(0) = 10, nên -9.8t + C1 = 10 suy ra V(t) = - 9,8t + 10

Vận tốc của tên lửa sau 5s là v(5) = -9,8 x 5 + 10 = 39 (m/s)

Những bài tập tự luyện về bảng nguyên hàm đầy đủ

Nhằm giúp các em hiểu hơn về các công thức nguyên hàm, hãy theo dõi và làm thử những bài tập dưới đây:

Phần 1: Bài tập cơ bản

Phần 2: Nguyên hàm từng phần

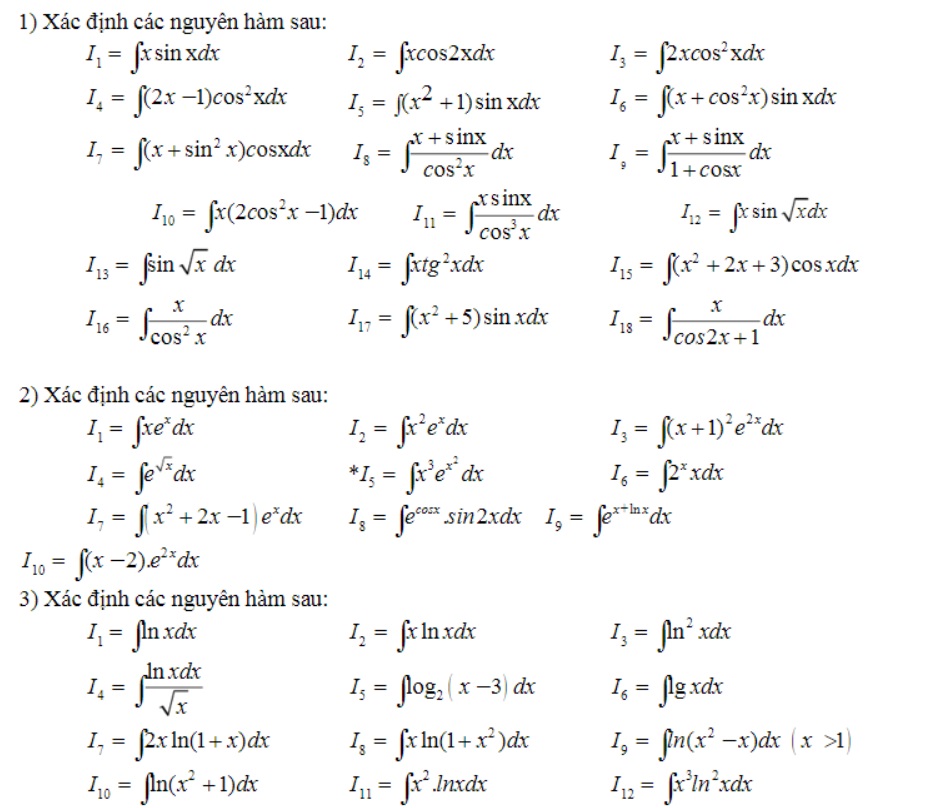
Một số ví dụ bài tập về bảng nguyên hàm mà các em có thể luyện tập tại nhà

Kết luận

Bài viết trên đã cung cấp bảng nguyên hàm đầy đủ mà các em sẽ gặp trong khi học, khi thi đại số. Thông qua những thông tin trên, thayphu mong muốn hỗ trợ các em học tập và ghi nhớ kiến thức nguyên hàm một cách dễ dàng và nhanh chóng hơn. Đừng quên, theo dõi những bài viết khác để quá trình học toán trở nên đơn giản hơn nhé.