Các dạng bài tập phương trình mặt cầu thường gặp bài thi toán 12

Các dạng bài tập Phương trình mặt cầu với công thức đơn giản giải nhanh trong toán học. Giúp đạt được điểm tuyệt đối trong những bài thi THPT quốc gia.

Phương trình mặt cầu là một trong số những kiến thức quan trọng trong chương trình học lớp 12. Nó xuất hiện ở tất cả các bài thi THPT quốc gia. Vậy nên các em bắt buộc phải nắm chắc các dạng bài tập phương trình mặt cầu để có thể giành được điểm tuyệt đối. Dưới đây là bài viết thayphu muốn chia sẻ đến các bạn về các dạng bài tập thường gặp.

Khái niệm phương trình mặt cầu

Công thức đơn giản dễ áp dụng

Khái niệm về mặt cầu

Mặt cầu tâm O bán kính r là : S(O;r) hoặc (S)

=> S(O;r) = {M|OM=r, r>0}

Phương trình mặt cầu

Giả sử mặt cầu (S) có tâm là (a,b,c) và bán kính R thì lúc này phương trình mặt cầu sẽ có dạng như sau:

• Phương trình rút gọn

( x - a)^2 + ( y - b)^2 + ( z - c)^2 = R ^2

• Phương trình khai triển

x^2 + y^2 + z^2 - 2ax - 2by - 2cz + d = 0

Lưu ý: phương trình khai triển được gọi là phương trình mặt cầu tâm I(a,b,c) bán kính R = √ a^2 + b^2 + c^2 - d khi

a^2 + b^2 + c^2 - d > 0

Đặc biệt: I ≡ 0 khi và chỉ khi phương trình thu gọn có x^2 + y^2 + c^2 = R^2 : sẽ được gọi là mặt cầu tâm O bán kính R

Ví dụ: Tìm tọa độ tâm và tính bán kính của mặt cầu (S)

( x - 3)^2 + ( y + 4)^2 + ( z - 2)^2 = 16

Lời giải

Tâm ( 3, -4, 2) bán kính R= 4

Các dạng bài tập phương trình mặt cầu thường gặp

Dưới đây là một số dạng bài tập về phương trình mặt cầu:

Dạng 1: Cần tìm tâm và bán kính của mặt cầu để đảm bảo rằng (S) thực sự là một mặt cầu.

Ở dạng bài tập này ta sẽ được xét theo dạng 2 phương trình sau :

,

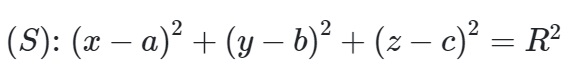
Phương trình có tâm I(a,b,c) và bán kính R

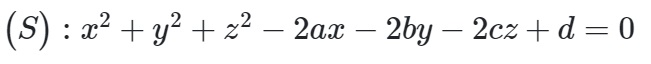
Phương trình có tâm I( a,b,c) và R = √ a^2 + b^2 + c^2 - d

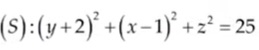
Ví dụ 1: Trong không gian Oxyz cho mặt cầu hãy tìm tọa độ tâm I và bánh kính R của mặt cầu (S)

Lời giải

Ta có : Tâm I(-2,1,0) và bán kính R = 5

Ví dụ 2: Trong không gian Oxyz cho mặt cầu : 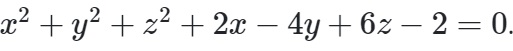Tìm tọa độ tâm I và bán kính R.

Lời giải

Dựa vào phương trình trên ta có:

I( 2/-2; -4/-2; 6/-2) = I( -1;2;-3)

Bán kính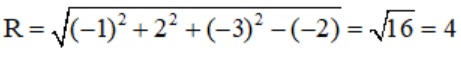

Dạng 2: Cho tâm I và bán kính R yêu cầu viết phương trình mặt cầu

Trong dạng bài tập này các em sẽ được cho trước những để bài sau:

Tâm I ( a;b;c)

Bán kính R

dựa vào những phần được cho trước để viết phương trình hoàn chỉnh

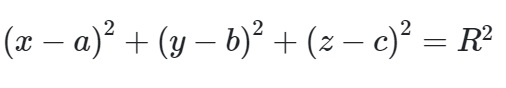
Ví dụ 1 : Trong mặt cầu Oxyz có điểm B( 2,1,3) Viết phương trình mặt cầu tâm B với R=4

Lời giải

Dạng phương trình này là :

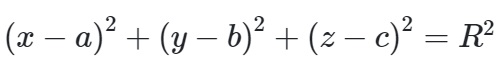
=> a= -2 , b= -1 , c= -3 và R= 16

Vậy ta có thể viết phương trình như sau : ( x - 2)^2 + ( y - 1)^2 + ( z - 3)^2 = 16

Ví dụ 2: Cho hai điểm A (-2; 1; 0) và B (2; -1; 2) trong không gian Oxyz. Hãy tìm phương trình của mặt cầu (S) có tâm là B và đi qua điểm A.

Lời giải

Mặt cầu có dạng phương trình :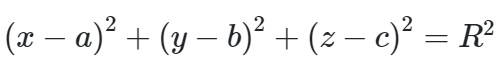

=> Tâm B ( 2;-1;2) có bán kính :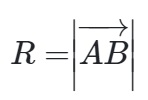

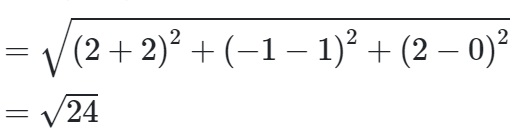
vậy phương trình mặt cầu sẽ được viết như sau:

( x -2)^2 + ( y + 1) ^ 2 + ( z - 2)^2 = 24

Dạng 3: Hãy viết phương trình của một mặt cầu có tâm tiếp xúc với một mặt phẳng.

Cho điểm I có tọa độ (a, b, c) và mặt phẳng được biểu diễn bởi phương trình Ax + By + Cz + D = 0. Vì mặt cầu tiếp xúc với mặt phẳng, chúng ta có thể suy ra rằng:

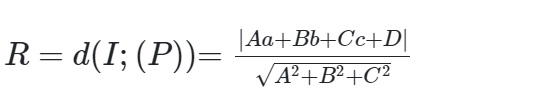
Ví dụ 1: Trong không gian có hệ tọa độ Oxyz, ta có điểm A có tọa độ (2; 1; 1) và mặt phẳng (P) có phương trình 2x – y + 2z + 1 = 0. Chúng ta cần tìm phương trình của mặt cầu có tâm A và tiếp xúc với mặt phẳng (P).

Lời giải

Bởi vì mặt phẳng (P) tiếp xúc với tâm A của mặt cầu, do đó bán kính của mặt cầu được xác định.

R = d(A;(P)) = |2.2 - 1+2.1+1|/ √ 2^2 + (-1)^2 + 2^2

=> phương trình mặt cầu sẽ là :

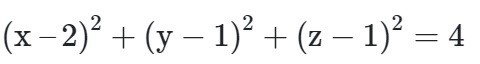
Dạng 4 : Cho phương trình hãy tìm các giá trị của m để (S) trở thành một phương trình của mặt cầu.

Ví dụ 1: Cho phương trình sau :

.

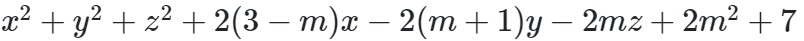Hãy tìm các giá trị của m để (S) trở thành một phương trình của mặt cầu.

Lời giải

Dạng 5: Hãy viết phương trình của một mặt cầu có tâm và tiếp xúc với một đường thẳng.

Cho hình vẽ sau

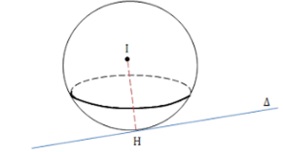
Cung cấp tọa độ I (a; b; c) và đường thẳng d.

Tìm tiếp điểm H của đường thẳng d trên mặt cầu có tâm I và bán kính R = IH của mặt cầu đó.

Ví dụ 1: Trong hệ tọa độ Oxyz, đang có một đường thẳng:

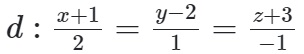
Một mặt cầu có tâm tại điểm I (1; -2; 3). Tìm phương trình mặt cầu tâm I và tiếp xúc với d:

Lời giải

Vẽ hình

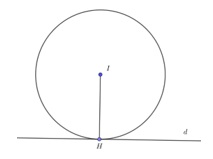
Đặt H là điểm tiếp xúc giữa đường tròn lớn có tâm I và đường thẳng d.

Vì H nằm trên d, ta có tọa độ của H là (-1 + 2t; 2 + t; -3 – t).

=>

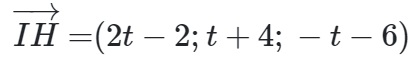
=> Vecto chỉ phương của đường thẳng d là :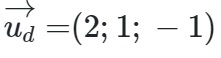

Vì IH vuông góc với d nên: 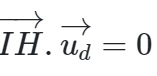⇔ (2t – 2).2 + (t + 4).1 + (-t – 6 ).(-1) = 0

=> t= - 1

Bán kính của mặt cầu được xác định bởi khoảng cách từ trung điểm của đường thẳng tới trung điểm của đoạn thẳng tiếp xúc với mặt cầu.

=> R = IH ⇔ 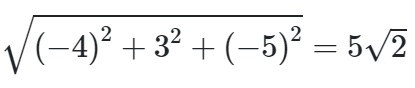Từ đây ta sẽ có phương trình:

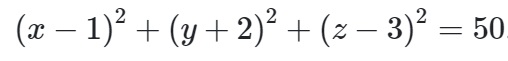
Dạng 6: Hãy viết phương trình của mặt cầu (S) khi biết tâm I và đường thẳng d cắt mặt cầu theo dây cung AB.

Giả sử đường thẳng d cắt mặt cầu (S) theo dây cung AB tại điểm M và N. Ta cần tìm phương trình của mặt cầu (S).

Để tìm phương trình của mặt cầu (S), ta cần biết bán kính của nó. Vì M và N đều nằm trên mặt cầu (S), nên ta có thể tính bán kính bằng cách tính độ dài của đoạn thẳng MN.

Sau đó, ta có thể sử dụng công thức phương trình mặt cầu trong hệ tọa độ Oxyz để tìm phương trình của mặt cầu (S).

Ví dụ 1: Viết phương trình mặt cầu (S) có tâm I (2; 3; -1) và cắt đường thẳng

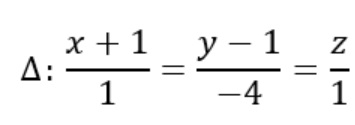
Ở hai điểm A và B, khoảng cách giữa chúng là 16 đơn vị.

Lời giải:

Vẽ hình

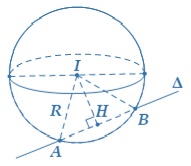
Nếu chọn điểm H (-1; 1; 0) trong tam giác Δ,

=> vector IH sẽ có giá trị là (3;2;1).

Một vectơ chỉ phương của đường thẳng Δ được cung cấp vecto u ( 1;-4;1)

Ta có IH vuông góc với AB <=> (t – 3).1 + (-4t – 2).(-4) + (t + 1).1 = 0

=> t=-⅓

=> tọa độ của vecto IH = ( -10/3; -⅔; ⅔) nên

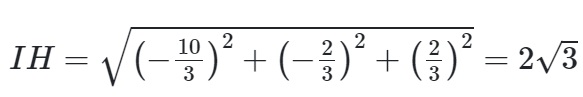
Vì AB=16 => HA = 1/2AB = 8

Dựa vào định lý pitago trong tam giác IAB ta có

IA^2 = IH^2 + HA^2 = (2√3)^2 + 8^2 = 76 => IA = 2√19

Vậy phương trình mặt cầu là :

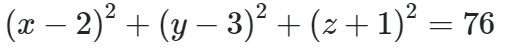
Dạng 7: Hãy viết phương trình của một mặt cầu (S) khi biết tâm (I) và khi mặt cầu cắt qua một mặt phẳng (P) tạo thành đường tròn (C) là giao tuyến.

Để giải bài toán, ta có thể sử dụng các bước sau:

• Tìm giao điểm của mặt phẳng (Q) và đường thẳng qua tâm I của mặt cầu (S). Điểm này chính là tâm O của hình tròn.
• Tính diện tích của hình tròn bằng công thức S = πR^2. Với giá trị diện tích đã cho, ta có thể tính được bán kính R.
• Sử dụng công thức phương trình mặt cầu trong hệ tọa độ Oxyz để tìm phương trình của mặt cầu (S) với tâm I và bán kính R đã tìm được ở bước 2.

Ví dụ 1: Hãy viết phương trình của mặt cầu (S) có tâm I (1; 0; 1) và phẳng (Q) có phương trình là 2x - y + z + 7 = 0 sao cho (Q) cắt (S) tạo thành một hình tròn với diện tích xác định là 20π.

Lời giải:

Ta có : d(I,(Q)) = 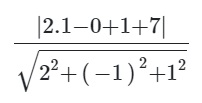= 5√6 / 3

Gọi r là bán kính của đường tròn giao tuyến (S), mặt phẳng (Q)

=> diện tích đường tròn ngoại tuyến 20п = пr^2 ⇔ r = 2√5

Cho R là bán kính mặt cầu (S)

=>

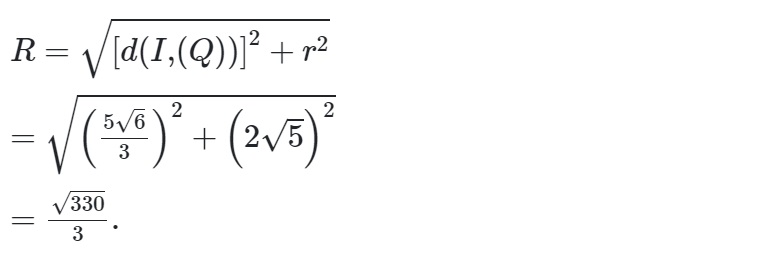
=> phương trình được viết như sau :

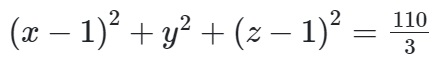
Dạng 8: Mặt cầu tâm nằm trên một mặt phẳng

Giả sử tâm I nằm trên đường thẳng ta được tham số hóa

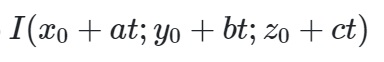
Lúc này tọa độ điểm I sẽ chỉ có một điểm t. Ta chỉ cần tạo ra một phương trình nữa từ đề bài là có thể tìm được I

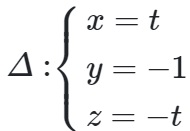
Ví dụ : cho tâm I nằm trên đường thẳng và (S) tiếp xúc với hai mặt phẳng α: x+ 2y+2z+3 =0 và β: x+2y+2z+7=0 .Hãy viết phương trình của một mặt cầu (S)

Lời giải:

Bài tập vận dụng về phương trình mặt cầu

Câu 4:

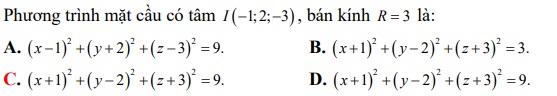
Câu 5:

Câu 6:

Câu 7:

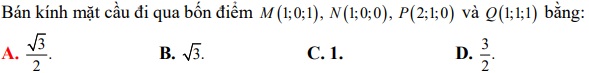
Câu 8:

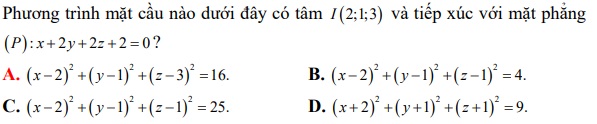
Câu 9:

Câu 10:

Kết luận

Trên đây là các dạng bài tập phương trình mặt cầu được dùng phổ biến nhất hiện nay. Hy vọng rằng sau khi đọc xong bài viết sẽ giúp các em có thể vận dụng tốt những bài tập trên. Đừng quên truy cập trang web của thayphu để có thể được điểm cao nhé!