Trọng tâm tứ diện là gì? Tính chất và cách xác định chi tiết

Trọng tâm tứ diện là một khái niệm quan trọng trong toán học và hình học. Cùng tìm hiểu định nghĩa, tính chất, cách xác định và các bài tập vận dụng của nó nhé.

Trọng tâm tứ diện là một dạng toán cơ bản và quan trọng trong chương trình Toán Hình học không gian 11. Bài viết này, thayphu sẽ giới thiệu đến các bạn học sinh Trọng tâm tứ diện là gì, tính chất và các phương pháp cần nắm để hiểu rõ khái niệm này. Song song đó là các bài tập mẫu để vận dụng thật tốt dạng toán này.

Trọng tâm tứ diện là gì? Định nghĩa chi tiết

• Trọng tâm tứ diện là một điểm nằm bên trong mặt phẳng của tứ diện sao cho tổng khoảng cách từ trọng tâm đến các đỉnh của tứ diện là nhỏ nhất.
• Trọng tâm tứ diện được xác định bằng cách lấy trung bình các tọa độ của các đỉnh. Hay nói cách khác, trọng tâm của tứ diện là giao điểm hai đường nối trung điểm của các cạnh đối diện nhau.
• Trọng tâm của tứ diện thường được ký hiệu bằng G.

Sau đây là bài toán ví dụ để các bạn có thể hiểu rõ hơn về khái niệm và bản chất của trọng tâm tứ diện.

Cho tứ diện ABCD mà điểm G có vị trí được xác định theo vectơ của các đoạn như sau: GA + GB + GC + GD = 0

Hãy chứng minh phương trình của vectơ các đoạn thẳng:

MA + MB + MC + MD = 4MG, với mọi M được xác định ( hay điểm G là trọng tâm của tứ diện ABCD).

Gợi ý lời giải:

Gọi I, J lần lượt là trung điểm của các đoạn AB, CD.

Ta có:

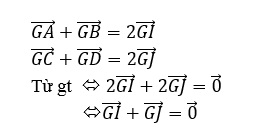
Vậy G là trung điểm của IJ ( hay G là trọng tâm của tứ diện ABCD) (điều phải chứng minh)

Tính chất trọng tâm tứ diện các em cần nắm

• Tính chất 1: Trọng tâm là trung điểm của các đường chéo: Trọng tâm tứ diện là trung điểm của các đường chéo của tứ diện. Có nghĩa là khoảng cách từ trọng tâm đến mỗi đỉnh của tứ diện là bằng nhau.
• Tính chất 2: Chia tứ diện thành các phần bằng nhau: Tính chất này chia tứ diện thành bốn phần có thể có diện tích và thể tích khác nhau. Tuy nhiên, bốn phần tứ diện này có cùng một trọng tâm.

Phương pháp xác định trọng tâm tứ diện bằng cách sử dụng các đoạn đường chéo

• Cách 1: Trọng tâm của tứ diện là giao điểm của hai đường chéo AC và BD. Ta vẽ hai đoạn thẳng AC và BD rồi tìm giao điểm của chúng để có được trọng tâm G.
• Cách 2: Đối với các tứ diện lồi (tứ diện có tất cả các góc nhọn), ta có thể vận dụng định lý trung điểm để xác định trọng tâm. Nghĩa là trọng tâm G của tứ diện là trung điểm của hai đường chéo AC và BD

Ví dụ minh họa:

Cho tứ diện ABCD và ta cần tìm trọng tâm của tứ diện.

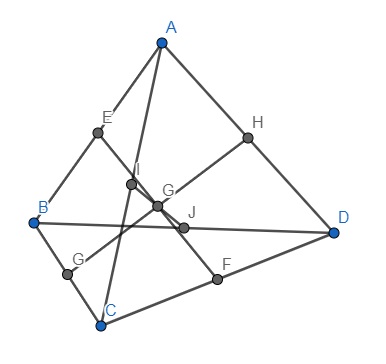
Gọi E, F, H, I, J, K lần lượt là trung điểm của các cạnh AB, CD, BC, AD, AC, BD.

Dựa vào định nghĩa, suy ra trọng tâm tứ diện là điểm giao của ba đường thẳng nối trung điểm của các cặp cạnh chéo đối nhau. Do đó, ta cần nối đường thẳng .

EF, GH, IJ.

Từ hình ảnh minh họa, ta có thể nhận ra rằng cả 3 đường thẳng EF, GH, IJ đều giao nhau tại điểm G

=> Ta gọi điểm G là trọng tâm của tứ diện ABCD.

Phương pháp xác định trọng tâm tứ diện bằng cách dùng trọng tâm tam giác đáy của tứ diện và một đoạn thẳng tỉ lệ

Phương pháp này ta có thể dùng linh hoạt hơn trong tất cả các loại tứ diện như tứ diện lồi hoặc lõm, không giống như phương pháp 1 chỉ có thể dùng được cho các tứ diện lồi. Vì vậy, phương pháp này dễ hiểu và dễ xác định trọng tâm hơn. Để xác định trọng tâm, ta thực hiện các bước sau đây:

• Bước 1: Xác định trọng tâm tam giác đáy của tứ diện đã cho
• Bước 2: Nối một đoạn thẳng từ đỉnh của tứ diện đến trọng tâm tam giác đáy
• Bước 3: Lấy 1 điểm trên đoạn thẳng vừa nối theo tỉ lệ ¾ từ đỉnh của tứ diện. Điểm cách đỉnh tứ diện ¾ đoạn thẳng (hoặc cách trọng tâm tam giác ¼) chính là trọng tâm tứ diện cần tìm.

Ví dụ minh họa:

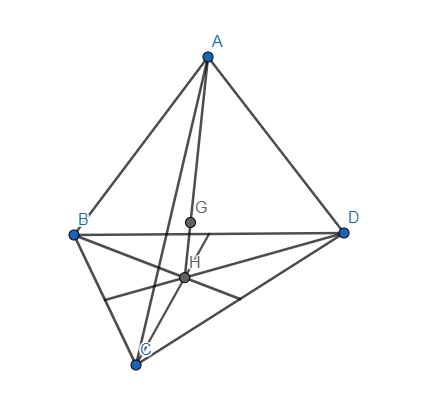
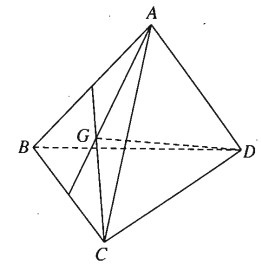
Cho tứ diện ABCD như hình minh họa, có tam giác đáy BCD.

Ta có trọng tâm H là giao điểm của các đường trung tuyến của tam giác đáy BCD.

Kẻ đoạn thẳng AH, trên đoạn AH đã có, lấy điểm G sao cho AG=3GH

Điểm G đã tìm được chính là trọng tâm tứ diện cần tìm.

Bài tập vận dụng dạng toán trọng tâm tứ diện (kèm lời giải chi tiết)

Bài tập 1: Cho tứ diện ABCD có G là trọng tâm của tam giác ABC, hãy chứng minh rằng:

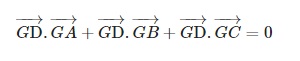
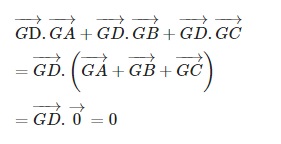
Bài tập 2: Cho tứ diện ABCD có G là trọng tâm của tam giác ABC. Chứng minh rằng:

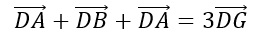
Gợi ý lời giải:

Dựa vào quy tắc ba điểm, ta có:

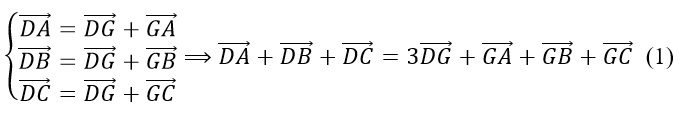
Mà điểm G là trọng tâm của tam giác ABC nên ta có:

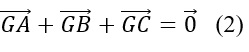
Từ ý (1) và (2), ta có thể suy ra:

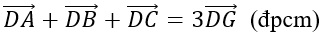
Qua bài viết này, thayphu đã giới thiệu cho các bạn học sinh về trọng tâm tứ diện, bao gồm định nghĩa, tính chất, cách xác định và các dạng bài tập cơ bản và phổ biến. Ta có thể thấy rằng Trọng tâm tứ diện là một khái niệm quan trọng trong Hình học không gian lớp 11, đặc biệt là nó có nhiều ứng dụng thực tế trong nhiều lĩnh vực khác nhau. Hy vọng rằng bài viết này đã cung cấp cho các bạn những kiến thức tổng quát về trọng tâm tứ diện và giúp bạn hiểu rõ hơn về khái niệm và tính chất của nó.