Phương pháp chứng minh hai mặt phẳng vuông góc chuẩn nhất

Chứng minh hai mặt phẳng vuông góc là khái niệm quan trọng trong hình học không gian. Đặc biệt, dạng toán này cũng xuất hiện nhiều trong các đề thi THPTQG.

Trong bài viết này thayphu sẽ tập trung vào việc chứng minh hai mặt phẳng vuông góc trong Toán hình học không gian 11. Chúng ta sẽ khám phá định nghĩa, điều kiện, các tính chất, các phương pháp chứng minh và cung cấp ví dụ minh họa để hiểu rõ hơn về tính chất đặc biệt này nhé.

Định nghĩa hai mặt phẳng vuông góc

2 mặt phẳng vuông góc là khi góc giữa của chúng bằng 90.

Kí hiệu: (P) (Q)

Tính chất

• Tính chất 1: Hai mặt cùng vuông góc với mặt phẳng thứ ba thì giao tuyến của nó cũng vuông góc với mặt đó.

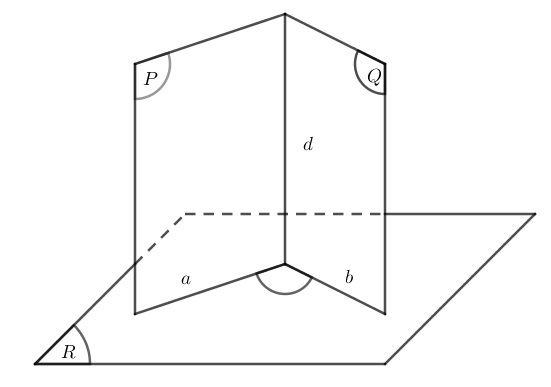
(P)(R)

(Q)(R)

(P)(Q)=d

d(R)

• Tính chất 2: Hai mặt phẳng vuông góc với nhau thì đường thẳng thuộc mặt này vuông góc với giao tuyến thì vuông góc với mặt còn lại.

()()

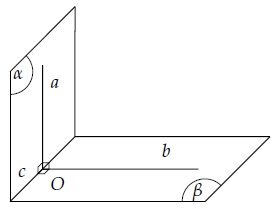
a()

ac=(P)(Q)

a()

Điều kiện để hai mặt phẳng vuông góc với nhau

Hai mặt phẳng vuông góc với nhau khi và chỉ khi 1 mặt phẳng chứa đường thẳng vuông góc với mặt còn lại.

Các phương pháp để chứng minh hai mặt phẳng vuông góc

Dạng 1: Chứng minh 1 đường thẳng vuông góc với mặt phẳng

• Cách 1: chọn 1 đường thẳng thuộc 1 mặt phẳng (ưu tiên mặt phẳng không chứa đường cao). Từ đó chứng minh đường thẳng vuông góc với mặt phẳng còn lại.
• Cách 2: Chứng minh góc giữa hai mặt phẳng đã cho bằng 90

Dạng 2: Chứng minh một đường thẳng vuông góc với mặt phẳng (để đường thẳng d(P) )

• Cách 1: Chứng minh đường thẳng d nằm trong mặt phẳng Q, với (Q)(P) và d vuông góc với giao tuyến của 2 mặt phẳng P và Q.

Cho 2 mặt phẳng vuông góc với nhau, nếu có 1 đường thẳng nằm trong mặt phẳng này vuông góc với giao tuyến của 2 mặt phẳng thì nó vuông góc với mặt phẳng còn lại.

(P)(Q), d(Q) và d vuông góc với giao tuyến của (P) và (Q)

d(P)

• Cách 2: Cho mặt phẳng (Q) và (R) cùng vuông góc với mặt phẳng (P) thì giao tuyến d của (Q)∩(R) sẽ vuông góc với (P)

d=(Q) ∩ (R) với (Q) ⊥ (P) và (R) ⊥ (P)

d(P)

Bài tập mẫu ứng dụng

Bài tập 1: Cho hình chóp S.ABCD có các mặt bên (SAB) và (SAD) cùng vuông góc với (ABCD). Biết ABCD là hình vuông. Chứng minh (SAB)(SBC).

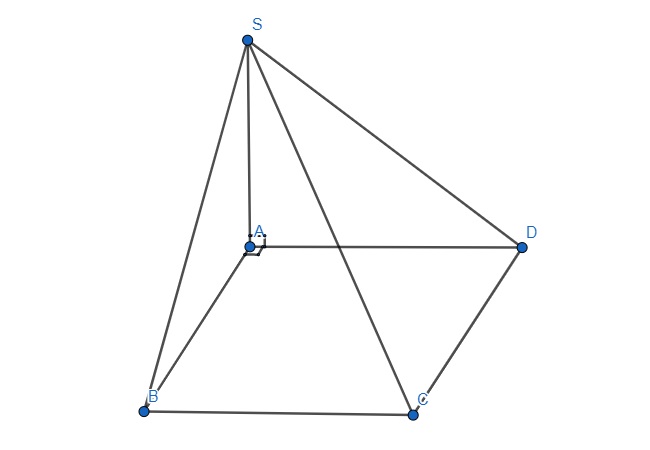
Gợi ý lời giải:

Vì các mặt bên (SAB) và (SAD) cùng vuông góc với (ABCD)

Ta có:

(SAB)(ABCD)

(SAD)(ABCD)

(SAB)(SAD)=SA

SA(ABCD)

Ta lại có: SABC và ABBC

BC(SAB) Mà BC(SBC)

(SBC)(SAB)

Vậy ta có thể kết luận mặt phẳng (SBC)(SAB).

Bài tập 2:

Cho hình chóp S.ABCD có đáy là hình thoi tâm O. Hai mặt phẳng (SAC) và (SBD) cùng vuông góc với đáy.

1. Chứng minh (SAC)(SBD)
2. Kẻ OKBC. Chứng minh (SBC)(SOK)

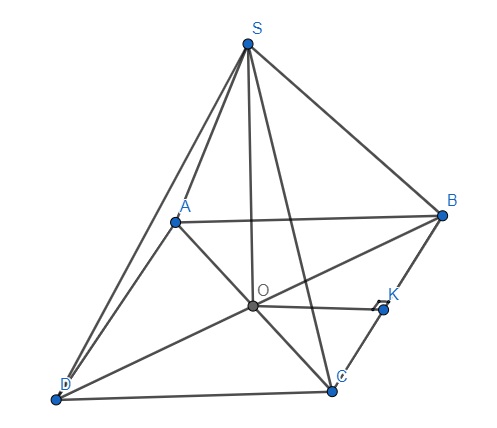
Gợi ý lời giải:

Từ giả thiết đề bài đã cho, ta có:

(SAC)(ABCD)

(SBD)(ABCD)

(SAC)(SBD)=SO

Từ đó ta suy ra: SO(ABCD)

a) (SAC)(SBD)

Ta có:

ACBD (do đáy là hình thoi)

ACSO (vì SO(ABCD))

AC(SBD)

Mà AC(SAC)

(SAC)(SBD)

b) (SBC)(SOK)

BCOK (đề đã cho)

BCSO (vì SO với đáy)

BC(SOK)

Mà BC(SBC)

Suy ra (SBC)(SOK)

Bài tập 3:

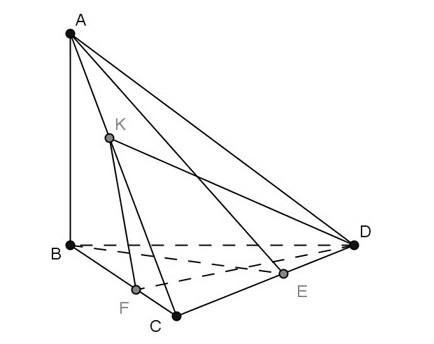
Cho tứ diện ABCD có hai mặt phẳng (ABC) và (ABD) cùng vuông góc với mặt phẳng (DBC). Gọi đoạn thẳng DF và BE lần lượt là hai đường cao của tam giác BCD, DK là đường cao của tam giác ACD. Trong các khẳng định dưới đây, khẳng định nào là sai?

1. (ABE)(ADC)

2. (ABD)(ADC)

3. (ABC)(DFK)

4. (DFK)(ADC)

Gợi ý lời giải:

• Ta có:

(ABC)(BCD)

(ABD)(BCD)

(ABC)(ABD)=AB

Suy ra AB(BCD)

Mặt khác:

CDBE

CDAB

CD(ABE) nên A đúng.

Ta lại có:

(ABC)(BCD)

(ABC)(BCD)=BC

DFBC

DF(ABC) vậy C đúng.

Ta có:

ACDF

ACDK

Suy ra AC(DKF) (ACD)(DKF). Vậy câu D đúng.

Từ đó ta có thể suy ra đáp án cần chọn là đáp án B.

Kết luận

Chứng minh hai mặt phẳng vuông góc là một dạng toán quan trọng trong hình học không gian, đặc biệt là chương trình Toán 11. Bài viết này đã giới thiệu các phương pháp chứng minh và cung cấp các bài tập ứng dụng để giúp bạn hiểu rõ hơn về khái niệm này. Hiểu về tính chất của mặt phẳng vuông góc và ứng dụng của nó có thể giúp bạn xác định và áp dụng chứng minh hai mặt phẳng vuông góc trong các bài toán hình học và các lĩnh vực liên quan.