Kiến thức về nhị thức newton cần nắm và bài tập áp dụng

Một số công thức nhị thức Newton áp dụng trong toán cấp 3 và tuyển sinh đại học, cùng tìm hiểu nhiều bài tập về nhị thức này kèm lời giải chi tiết!

Công thức nhị thức Newton nằm trong chương trình giảng dạy lớp 11, là công thức nền tảng cho các dạng bài tập toán lớp 12 và tuyển sinh đại học. Với những kiến thức toán học cùng bài tập có lời giải chi tiết sẽ giúp người đọc, đặc biệt là các bạn học sinh sẽ nắm được một cách đơn giản.

Bài viết dưới đây của thayphu sẽ chia sẻ những kiến thức liên quan đến dạng công thức này kèm theo một vài bài tập có lời giải để bạn tham khảo.

Tìm hiểu về nhị thức Newton

Nhị thức Newton là gì?

Nhị thức Newton còn được gọi với cái tên định lý nhị thức là một công thức khai triển hàm mũ của tổng doi nhà toán học - cơ học Isaac Newton tìm ra vào năm 1665. Công thức toán học này đã trở nên phổ biến và được áp dụng giảng dạy trong chương trình học hiện nay. Ngoài Isaac Newton, định lý toán học này còn được độc lập chứng minh bởi nhà toán học James Gregory vào năm 1670.

Công thức nhị thức Newton

Công thức nhị thức Newton là gì?

Khai triển ( a + b)n được cho bởi công thức như sau:

Với a, b là số thức và n là số nguyên dương, ta có:

Ta được quy ước a0 = b0 = 1

Hệ quả của công thức:

Tính chất công thức nhị thức Newton

• Các số hạng của công thức là n + 1
• Tổng số mũ của a và b trong mỗi số hạng sẽ luôn bằng số mũ của nhị thức:

( n – k) + k = n

• Số hạng tổng quát của nhị thức sẽ là:

Tk+1 = Cnk an-k bk ( Đó là số hạng thứ k + 1 trong khai triển ( a + b)n )

• Các hệ số nhị thức cách đều hai số hạng đầu, cuối thì bằng nhau

Một số kiến thức liên quan đến nhị thức Newton

Ngoài công thức và tính chất của nhị thức Newton, bài viết còn nêu một số kiến thức liên quan đến nhị thức Newton được chia sẻ chi tiết như sau để bạn tham khảo:

• Công thức khai triển của nhị thức newton là:

• Công thức số tổ hợp là:

*

• Tính chất lũy thừa là:

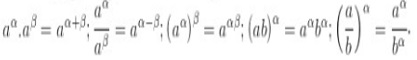
Các dạng bài tập về nhị thức Newton kèm lời giải chi tiết

Việc tìm hiểu công thức với mục đích cuối cùng là áp dụng được vào bài tập và đưa ra kết quả cuối cùng chính xác nhất. Nắm được công thức nhưng chưa chắc học sinh sẽ áp dụng tốt các công thức này vào các bài toán liên quan. Dưới đây là 10 bài tập có lời giải chi tiết liên quan đến nhị thức Newton đã được liệt kê để bạn tham khảo. Hy vọng với các lời giải chi tiết này bạn sẽ hiểu được và áp dụng thành công các nhị thức toán học này vào bài tập.

Bài tập 1

Giải bất phương trình ( A22x – A2x < = ( 6/ x). C3x + 10

Giải:

Điều kiện là x phải là một số nguyên dương và x > = 3

Ta có bất phương trình đã cho sẽ tương đương với:

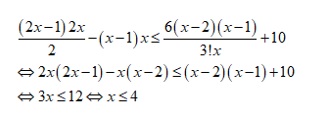
X là nghiệm nguyên dương và x > = 3 nên suy ra x thuộc {3 ; 4}

Bài tập 2

Tìm hệ số của x5 trong khai triển của biểu thức dưới đây:

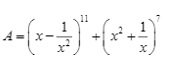
Giải:

Công thức khai triển của biểu thức trên là:

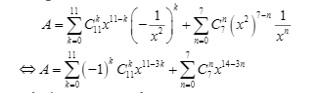
Để số hạng chứa x5 vậy suy ra k = 2 và n = 3

Vậy hệ số của x5 sẽ là C211 + C37 = 90

Bài tập 3

B = 2n C0n – 2n-1 C1n + 2n-2 C2n + … + (-1)k 2n-k Ckn + … + (-1)2 Cnn

Giải:

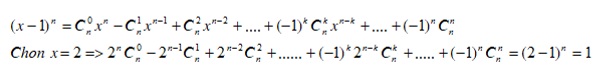
Bài tập 4

Tìm hệ số của x5 trong khai triển đa thức của: x(1 – 2x)5 + (1 + 5x)10

Triển khai: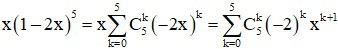

Triển khai: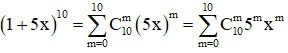

Do đó: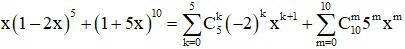

Cần tìm hệ số của x5 trong khai triển thì ta có: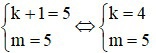

Suy ra hệ số của đa thức trong khai triển là: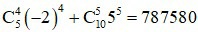

Bài tập 5

Tính hệ số x10y8 trong khai triển ( x + y)18

Giải:

Theo công thức nhị thức Niu- tơn, hệ số x10y8 là: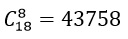

Bài tập 6

Tìm hệ số của x4 trong khai triển ( 2x- 5)7

Giải:

Ta có: (2x – 5)7 = [ (2x + (-5)]7

Theo công thức nhị thức Niu-tơn; số hạng chứa x4 là: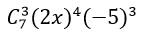

Do đó hệ số của x4 là: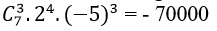

Các dạng bài tập liên quan đến nhị thức newton khá khó hiểu, dù đã áp dụng công thức và có hướng dẫn giải chi tiết từng bài tập thì chưa chắc các bạn học sinh sẽ nắm được. Việc học toán là sự đầu tư thời gian và chất xám để nghiên cứu công thức và cách giải, có vậy bạn mới nắm được nhuần nhuyễn công thức và cách áp dụng chúng vào bài tập toán.

Bài tập 7

Tìm hệ số x15 trong khai triển đẳng thức sau:

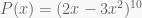
Giải:

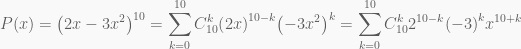
Số hạng K thỏa mãn: 10 + K = 15 suy ra K = 5

Kết quả của hệ số x15 là: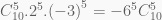

Bài tập 8

(D-04) Tìm kết quả số hạng không chứa x trong khai triển đa thức của biểu thức:

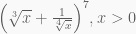
Giải:

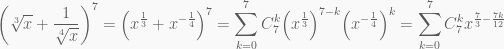
Số hạng không chứa x tương ứng số hạng chứa k thỏa mãn điều kiện:

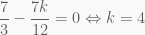
Vậy kết quả số hạng không chứa x là:

Bài tập 9

(A-03) Tìm kết quả hệ số của số hạng chứa x^8 trong khai triển:

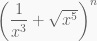biết rằng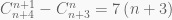

Giải:

Theo đề ta có: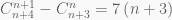

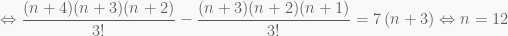
Từ đó: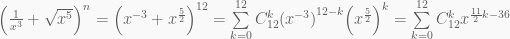

Số hạng chứa x5 tương ứng với số hạng chứa k thỏa mãn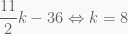

Vậy kết quả số hạng không chứa x là:

Bài tập 10

(D-02) Tìm kết quả số nguyên dương n thỏa mãn hệ thức sau:

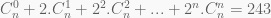
Giải:

Xem khai triển hệ thức: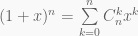

Cho x = 2 ta được: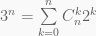

Theo giả thiết ta có: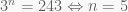

Kết quả cuối cùng là: n = 5

5 dạng bài tập về nhị thức newton được trình bày và giải chi tiết phía trên đều là những dạng bài cơ bản để người mới học có thể nắm bắt và theo kịp. Hy vọng thông qua các bài tập về nhị thức newton, người đọc sẽ phần nào nắm được dạng công thức này và thật sự hiểu nó khi áp dụng vào bài tập.

Kết bài

Bài viết trên là những kiến thức toán học đầy đủ nhất được tác giả chia sẻ, bao gồm một vài bài tập mẫu kèm lời giải chi tiết đã được trình bày. Các bạn học sinh đang có nhu cầu tìm hiểu về nhị thức Newton thì không nên bỏ qua bài viết bổ ích này. Mục tiêu của bài viết là đem đến những thông tin tin bổ ích về kiến thức cho người đọc, thành công khi người đọc hiểu được các thông tin kiến thức đã nêu và áp dụng được vào bài tập để đưa ra được kết quả cuối cùng chính xác nhất.