Công thức đạo hàm của hàm số lượng giác và bài tập áp dụng

Công thức tính đạo hàm của hàm số lượng giác, bảng tóm tắt công thức từ cơ bản đến nâng cao và các bài tập vận dụng cụ thể của đạo hàm.

Trong toán học, đạo hàm của hàm số lượng giác là một khái niệm quan trọng trong Toán đại số và giải tích. Nó giúp chúng ta hiểu sự biến thiên của các hàm số lượng giác như sin(x), cos(x), và tan(x). Và trong bài viết này, thayphu sẽ giới thiệu đến các bạn học sinh về đạo hàm của các hàm số lượng giác, công thức đạo hàm và các bài tập ví dụ minh họa chi tiết nhất.

Đạo hàm của hàm số lượng giác là gì?

Đạo hàm của hàm số lượng giác là một công cụ để nghiên cứu tốc độ biến thiên của các hàm số lượng giác như sin(x), cos(x), và tan(x). Nó giúp chúng ta hiểu rõ hơn về cách mà giá trị của các hàm số này thay đổi khi giá trị đầu vào thay đổi.

Công thức tính đạo hàm lượng giác

• Đạo hàm của hàm sin(x):

Hàm số sin(x) biểu diễn mối quan hệ giữa một góc và tỉ lệ giữa độ dài của cạnh đối và cạnh huyền trong một tam giác vuông.

Công thức tính đạo hàm của sin(x) là:

(sin(x))’ = cos(x)

Nó cho chúng ta biết tốc độ biến thiên của sin(x) tại mỗi điểm. Giá trị của cos(x) sẽ tăng dần từ -1 đến 1 khi x tăng, và giảm dần từ 1 về -1 khi x giảm.

• Đạo hàm của hàm cos(x):

Hàm số cos(x) biểu diễn mối quan hệ giữa một góc và tỉ lệ giữa độ dài của cạnh kề và cạnh huyền trong một tam giác vuông.

Công thức tính đạo hàm của cos(x) là:

(cos(x))’ = -sin(x)

Nó cũng cho chúng ta thông tin về tốc độ biến thiên của cos(x) tại mỗi điểm. Giá trị của -sin(x) sẽ giảm dần từ -1 đến 1 khi x tăng, và tăng dần từ 1 về -1 khi x giảm.

• Đạo hàm của hàm tan(x):

Hàm số tan(x) biểu diễn mối quan hệ giữa một góc và tỉ lệ giữa độ dài của cạnh đối và cạnh kề trong một tam giác vuông.

Công thức tính đạo hàm của tan(x) là:

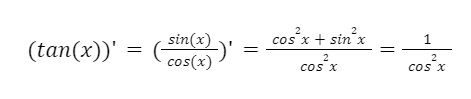
Nó cung cấp cho chúng ta thông tin về tốc độ biến thiên của tan(x) tại mỗi điểm. Giá trị của 1/cos^2x luôn là dương và không có giới hạn khi x thay đổi.

• Đạo hàm của hàm cot(x):

Ngược lại với hàm tan(x), hàm số cot(x) biểu diễn mối quan hệ giữa một góc và tỉ lệ giữa độ dài của cạnh kề và cạnh đối trong một tam giác vuông.

Công thức tính đạo hàm của cot(x) là:

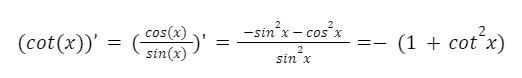
Nó cung cấp cho chúng ta thông tin về tốc độ biến thiên của tan(x) tại mỗi điểm. Giá trị của -(1+cot^2x) luôn là dương và không có giới hạn khi x thay đổi.

Bảng đạo hàm từ cơ bản đến nâng cao của hàm số lượng giác

Dưới đây là bảng công thức cơ bản của đạo hàm hàm số lượng giác, giúp các bạn giải nhanh hơn các dạng bài tập về đạo hàm.

Ngoài ra còn có một bảng tổng hợp cụ thể và chi tiết từ cơ bản đến nâng cao của đạo hàm lượng giác như bảng dưới đây:

Bài tập vận dụng đạo hàm của hàm số lượng giác

Bài tập 1: Tính đạo hàm của các hàm số sau đây:

1. y = sin2x.cos^4x - cot(1/x^2) - sin2x.sin^4x
2. y = tan(2x + 1) - x.cos^2x

Gợi ý lời giải:

1. y = sin2x.cos^4x - cot(1/x^2) - sin2x.sin^4x

= sin2x. (cos^4x - sin^4x) - cot(1/x^2)

Do đó:

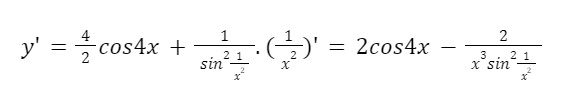
2. y = tan(2x + 1) - x.cos^2x

y’= 2/cos^2(2x + 1) - (cos^2x - 2x.sinx.cosx)

= 2/cos^2(2x + 1) - cos^2x + x.sin2x

Bài tập 2: Tìm đạo hàm của các hàm số đã cho

1. f(x) = sin2x -cos^2(3x)
2. f’(x) = 2cos2x + 3sin6x
3. f’(x) = 2cos2x - 3sin6x
4. f’(x) = 2cos2x - 2sin3x
5. f’(x) = cos2x + 2sin3x

f’(x)= (sin2x -cos^2(3x))’= 2cos2x + 3sin3x.2cos3x = 2cos2x + 3sin6x

Chọn đáp án A.

2. f(x) = cos^2(3x)

1. f’(x) = 3sin6x

2. f’(x) = sin6x

3. f’(x) = -3sin6x

4. f’(x) = -sin6x

f’(x) = (cos^2(3x))’ = -6sin3x.cos3x = -3sin6x

Chọn đáp án C.

3. f(x) = cos4x - 3sin4x

1. f’(x) = 12cos4x + 4sin4x

2. f’(x) = -12cos4x + 4sin4x

3. f’(x) = -12cos4x - 4sin4x

4. f’(x) = -3cos4x - sin4x

f’(x) = (cos4x - 3sin4x)’= -4sin4x - 12cos4x

Chọn đáp án C.

4. f(x) = cos2x + 1

1. f’(x) = -sin2x

2. f’(x) = 2sin2x

3. f’(x) = -2sin2x + 1

4. f’(x) = -2sin2x

Phương pháp: (coskx)’= -ksinkx

f’(x) = (cos2x + 1)’= -2sin2x

Chọn đáp án D.

5. f(x) = x^2.cosx

1. f’(x) = 2xsinx - x^2.cosx

2. f’(x) = 2xsinx + x^2.cosx

3. f’(x) = 2xcosx - x^2.sinx

4. f’(x) = 2xcosx - x^2.sinx

f’(x) = (x^2.cosx)’ = 2x.cosx - x^2.sinx

Chọn đáp án C.

6. f(x) = cos2x. Tính P = f’’(π)

1. P = 4

2. P = 0

3. P = -4

4. P = -1

Phương pháp: (cosu)’= -u’.sinu; (sinu)’= u’.cosu

Ta có: f’(x)= -2sin2x => f’’(x) = -4cos2x

=> P = f’’(π) = -4

Chọn đáp án C.

Kết luận

Thông qua các đạo hàm này, chúng ta đã có thể nắm bắt được các đặc điểm quan trọng của các hàm số lượng giác, cách tính đạo hàm của hàm số lượng giác và các bài tập vận dụng cùng lời giải chi tiết. Tóm lại, đạo hàm của hàm số lượng giác là một khái niệm quan trọng trong toán học và có nhiều ứng dụng rộng rãi. Nắm vững kiến thức này giúp chúng ta hiểu rõ hơn về tốc độ biến thiên của các hàm số lượng giác và áp dụng chúng vào các bài toán thực tế. Đặc biệt đây là dạng toán quan trọng, trọng tâm thường xuất hiện trong các đề thi quan trọng, Vì vậy các em hãy ôn luyện thật kỹ, thật chắc dạng toán này nhé.