Nắm công thức cấp số cộng, cấp số nhân chuẩn trong 5 phút

Nắm vững công thức cấp số cộng cấp số nhân chuẩn theo sách giáo khoa, kèm một số bài tập áp dụng có lời giải cực chi tiết và dễ hiểu.

Nhắc đến môn toán, người ta sẽ nghĩ ngay đến các công thức cùng các con số đi kèm. Môn toán đòi hỏi người học phải có tư duy logic và khả năng phân tích tốt để đưa ra kết quả chính xác cuối cùng chỉ với công thức và các con số đã cho trước.

Ở bài học này, các bạn có thể tham khảo về công thức cấp số cộng cấp số nhân cực kỳ chi tiết trong chương trình học của các em học sinh lớp 11, kèm theo các bài tập có lời giải chi tiết. Hãy cùng thayphu tìm hiểu bài học ngay sau đây!

Chi tiết công thức cấp số cộng và cấp số nhân

Công thức của cấp số cộng, cấp số nhân là gì?

Trước khi tìm hiểu chi tiết về công thức, ta cần tìm hiểu về khái niệm đầu tiên. Hiểu được khái niệm giúp học sinh dễ dàng tiếp thu được công thức một cách dễ dàng mà không phải hiểu theo kiểu học vẹt.

Công thức cấp số nhân

• Khái niệm cấp số nhân là gì?

Cấp số nhân là một dãy số (gồm các số hữu hạn hoặc vô hạn), trong đó kể từ số hạng thứ hai, mỗi số hạng đều là tích của số hạng đứng trước nó với một số không đổi là q với q là công bội của cấp số nhân. Hằng số này được gọi là công bội của cấp số nhân đó.

• Tính chất của cấp số nhân

Ta có u2k=uk–1.uk+1,∀k≥2

Số hạng tổng quát là un=u1.qn–1,n≥2.

Tổng n số hạng đầu là Sn=u1+u2+…+un=u1(1–qn)1–q

Khi q = 0 thì dãy số sẽ là u1;0;0;…;0;… và Sn=u1

Khi q = 1 thì dãy số có dạng u1;u1;u1;…;u1;…và Sn=n.u1

Khi u1=0 thì với mọi q, cấp số nhân có dạng là 0;0;0;…;0;…và Sn=0

• Công thức tổng quát cấp số nhân

Un+1 = Un.q

Trong đó: n ∈ N*, công bội là q, hai số liên tiếp trong công bội là Un, Un+1

Công thức cấp số cộng

• Khái niệm cấp số cộng là gì?

Cấp số cộng là một dãy số thoả mãn điều kiện như sau: Hai phần tử liên tiếp nhau sai khác nhau một hằng số. Chẳng hạn với dãy số 3, 5, 7, 9, 11,... là một cấp số cộng với các phân tử liên tiếp sai khác nhau hằng số 2.

• Tính chất của cấp số cộng

Ta có Un+1 – Un = Un+2 – Un+1

Nếu như có 3 số bất kì m, n, q lập thành cấp số cộng thì 3 số đó luôn thỏa mãn m + q = 2n

Số hạng tổng quát là Un = U1 + d(n−1)

Muốn tính tổng n số hạng đầu, ta có công thức:

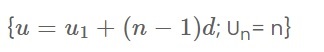
• Công thức tổng quát cấp số cộng

Un+1 = Un + d với ∀n ∈ N*

Trong đó : Với d được gọi là công sai, Un+1 – Un = d với mọi n ∈ N* ( trong đó d là hằng số còn Un+1; Un là hai số liên tiếp của dãy số CSC). Khi hiệu số Un+1 – Un phụ thuộc vào n thì không thể là cấp số cộng.

Bài tập về công thức cấp số cộng cấp số nhân kèm lời giải

Bài tập về cấp số cộng, cấp số nhân

Bài tập kèm lời giải sẽ giúp bạn hiểu hơn về công thức cấp số cộng cấp số nhân. Việc áp dụng công thức vào bài tập thực tế giúp bạn nắm được công thức và dễ dàng tiếp thu hơn so với việc học thuộc vẹt, Dưới đây là một vài bài tập kèm lời giải về công thức này.

Bài tập 1

Đề cho cấp số cộng (un) với u1 = 3, u2 = 9. Thực hiện tính công sai của cấp số cộng đã cho.

Giải:

Cấp số cộng Un với số hạng tổng quát Un = U1 + d(n−1)

Trong đó số hạng đầu U1 và công sai d

Từ đó ta có được U2 = U1 + d ⇔ 9 = 3 + d ⇔ d = 6

Vậy suy ra công sai của cấp số cộng này là 6.

Bài tập 2

Đề cho cấp số nhân (un) với u1=–2; q = – 5. Viết 3 số hạng tiếp theo và số hạng tổng quát của cấp số nhân un.

Giải:

Ta có u2=u1.q=(–2).(–5)=10;u3=u2.q=10.(–5)=–50;u4=u3.q=–50.(–5)=250

Số hạng tổng quát của un=u1.qn–1=(–2).(–5)n–1.

Bài tập 3

Đề cho cấp số nhân (un) với u1=–12; u7=–32. Tìm q?

Giải:

Áp dụng công thức số hạng tổng quát cấp số nhân ta có được:

un=u1qn–1⇒u7=u1.q6⇒q6=64⇒[q=2q=–2

Bài tập 4

Chứng minh rằng dãy số 1,−3,−7,−11,−15 là một cấp số cộng.

Giải:

Theo đề ta có:

−3=1+(−4) ; −11=−7+(−4);

−7=−3+(−4); −15=−11+(−4);

Suy ra dãy số 1,−3,−7,−11,−15 là một cấp số cộng với công sai d=−4.

Bài tập 5

Tìm bốn số hạng liên tiếp của một cấp số cộng biết rằng tổng của chúng là bằng 20 và tổng các bình phương của chúng là bằng 120.

Giải:

Ví dụ bốn số hạng đó lần lượt là a – 3x, a – x, a + x, a + 3x với công sai là d = 2x. Khi đó, ta có:

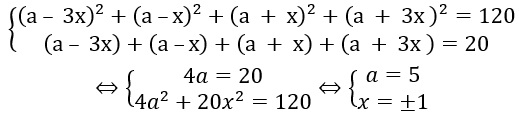
Bộ số cần tìm là 2,4,6,8.

Bài tập 6

Chứng minh rằng dãy số (un) với un = 17n + 2 là một cấp số cộng

Giải:

un+1 = 17(n + 1) + 2 = 17n + 19

Suy ra hiệu: un+1 – un = (17n + 19) − (17n + 2) = 17

=> (un) là cấp số cộng với công sai d = 17.

Bài tập 7

Chứng minh rằng dãy số (un) với un = 10 − 5n là một cấp số cộng.

Giải:

un+1 = 10 − 5(n+1)= 5 − 5n.

Xét về hiệu: un+1 − un = (5 − 5n) − (10 − 5n) = −5

Suy ra (un) là cấp số cộng với công sai d = −5.

Điểm chung của những bài tập kèm lời giải chi tiết về công thức cấp số cộng cấp số nhân là đều áp dụng công thức hoặc giả sử số bất kì để đưa ra kết quả chính xác cuối cùng. Việc nắm được công thức giúp bạn dễ dàng giải mã được các bài tập khó nhằn nhất. Với bài tập và lời giải chi tiết liên quan đến cấp số nhân và cấp số cộng đã được trình bày sẽ giúp người học dễ dàng tiếp thu công thức và thực hiện áp dụng tính toán thành công.

Kết luận

Bài viết trên là những thông tin và kiến thức liên quan đến công thức cấp số cộng cấp số nhân được chia sẻ để bạn tham khảo. Hy vọng với những thông tin được chia sẻ và một vài bài tập kèm lời giải chi tiết sẽ giúp học sinh nắm được dạng công thức này.