Đạo hàm là gì? Bảng đạo hàm đầy đủ và bài tập áp dụng

Bảng đạo hàm cơ bản là công cụ giúp các bạn học sinh giải các bài tập nhanh và dễ dàng. Ứng dụng và các dạng bài tập vận dụng khác nhau của bảng đạo hàm.

Bảng đạo hàm cung cấp cho chúng ta các thông tin quan trọng về công thức và đặc điểm của hàm số. Ngoài ra, nó cũng giúp chúng ta xác định các điểm cực trị (điểm cực đại và cực tiểu) và các điểm uốn cong của đồ thị hàm số. Đồng thời, bảng đạo hàm cũng hỗ trợ trong việc giải các bài toán tối ưu, xác định điểm cực trị tối ưu của hàm số.

Trong bài viết này, thayphu sẽ giới thiệu đến các bạn học sinh bảng đạo hàm cơ bản, ứng dụng và các bài tập vận dụng liên quan nhé.

Đạo hàm là gì?

• Đạo hàm là một khái niệm trong toán học, đặc biệt trong phân tích toán học, nó mô tả tốc độ biến thiên của một hàm số tại mỗi điểm trên miền xác định của nó. Đạo hàm cho ta biết về cách mà giá trị của một hàm số thay đổi khi giá trị đầu vào thay đổi.
• Đạo hàm có thể được hiểu như độ dốc của đường cong biểu diễn bởi hàm số tại mỗi điểm. Nếu đạo hàm dương tại một điểm, hàm số đang tăng lên. Nếu đạo hàm âm tại một điểm, hàm số đang giảm. Đạo hàm cũng giúp xác định các điểm cực trị của hàm số, bao gồm các điểm cực đại và cực tiểu.

Công thức đạo hàm

Đạo hàm của một hàm số f(x) được ký hiệu là f’(x) hoặc y’(x).

Cách tính đạo hàm khái quát được biểu diễn bằng công thức:

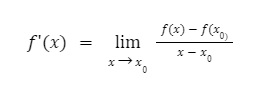
Bảng đạo hàm cơ bản

Sau đây là bảng tổng hợp các công thức đạo hàm cơ bản trong Toán đại số và giải tích 11 để các bạn học sinh dễ dàng vận dụng vào các dạng toán khác nhau.

Ứng dụng của bảng đạo hàm

• Bảng đạo hàm là công cụ cơ bản trong việc giải các bài toán tối ưu, từ tìm điểm cực trị đến xác định điểm tối ưu của một hàm số. Nó cung cấp thông tin về tính chất và biến đổi của hàm số, giúp chúng ta nắm bắt được khái niệm về đạo hàm và ứng dụng của nó trong các phương trình đạo hàm riêng.
• Phân tích hình dạng hàm số: Bảng đạo hàm cung cấp thông tin về tốc độ biến đổi và đặc điểm của một hàm số. Nó giúp chúng ta xác định các điểm uốn cong, điểm cực trị và đánh giá hình dạng của đồ thị. Thông qua đạo hàm, ta có thể biết được hàm tăng hay giảm và ước lượng độ lớn của sự biến đổi.
• Trong kinh tế, nó hỗ trợ trong việc đánh giá biến động và tăng trưởng của các chỉ số kinh tế, từ lợi nhuận đến tỷ suất tăng trưởng.
• Trong tài chính, nó được sử dụng để tính toán tỷ suất sinh lời, rủi ro đầu tư và các chỉ số tài chính khác.

Các bài tập vận dụng của bảng đạo hàm

Bài tập 1: Tìm phương trình y’ = f’(x) = 0 của các phương trình sau đây:

1. y = x^3 - 3x^2
2. y = 4x^3 - 12x^2 + 9x - 1

Gợi ý lời giải:

1. Ta có: y’ = (x^3 - 3x^2)’ = 3x^2 - 6x

Suy ra y’ = 0 ⇔ 3x^2 - 6x = 0 ⇔ x = 0, x = 2

Vậy phương trình y’= 0 có 2 nghiệm phân biệt x = 0 và x = 2.

2. Ta có: y’= (4x^3 - 12x^2 + 9x - 1)’= 12x^2 - 24x + 9

Suy ra y’ = 0 ⇔ 12x^2 - 24x + 9 = 0 ⇔ x = 3/2, x = ½

Vậy phương trình y’= 0 có hai nghiệm phân biệt x = 3/2 và x = ½.

Bài tập 2: Cho hàm số y = x^3 + 3mx^2 + ( m + 1)x + 1, trong đó m là một tham số thực. Tìm giá trị của m để tiếp tuyến của đồ thị hàm số đã cho tại điểm có hoành độ x = -1 và đi qua điểm A(1;2).

Gợi ý lời giải:

TXĐ: D = R

y’ = f’(x)= 3x^2 + 6mx + m + 1

Với x0 = -1 => y0 = 2m - 1, f’( -1) = -5m + 4

Phương trình tiếp tuyến tại M (-1; 2m – 1) : y= ( -5m + 4 )( x+1) + 2m -1 (d)

Ta có điểm A(1;2) ∈ (d) ⇔ (-5m + 4).2 + 2m – 1 = 2

Vậy suy ra m = ⅝

Bài tập 3: Hàm số y = x^3 +3x^2 – 9x + 5 ( C). Hãy tìm tiếp tuyến của đồ thị hàm số có hệ số góc nhỏ nhất trong tất cả các tiếp tuyến của đồ thị (C ).

Gợi ý lời giải:

Ta có y’ = f’( x ) = 3x^2 + 6x – 9

Gọi x0 là hoành độ tiếp điểm của tiếp tuyến, vậy ta có f’( x0) = 3x^2 + 6x – 9

Ta có: 3x^2 + 6x– 9 =3(x^2 + 2x +1) – 12 = 3(x+1).2 – 12 > – 12

Vậy suy ra min f(x0) = -12 tại x0= -1 => y0 = 16

Từ đó suy ra phương trình tiếp tuyến cần tìm: y = -12(x+1) + 16 ⇔ y = -12x +4

Kết luận

Bài viết này đã cung cấp cho các bạn học sinh tổng hợp đầy đủ các khái niệm, công thức, ứng dụng và các bài tập ôn tập của đạo hàm. Từ đó, ta có thể thấy được vai trò quan trọng của bảng đạo hàm trong toán học, đặc biệt là Toán đại số và giải tích 11. Đạo hàm là kiến thức trọng tâm quan trọng, vì vậy các em hãy luyện tập thật nhiều để nắm vững các dạng bài tập của đạo hàm nhé. Bởi lẽ đây là dạng toán sẽ xuất hiện rất nhiều trong các câu ở mức độ cơ bản của các đề thi.