Cách tìm chu kì của hàm số lượng giác và bài tập áp dụng

Cùng tìm hiểu định nghĩa, xem xét các tính chất, các phương pháp quan trọng và khám phá ứng dụng của chu kỳ hàm số trong Toán hình học lớp 11.

Bạn muốn hiểu về khái niệm chu kì của hàm số và cách nó được áp dụng trong các lĩnh vực như Toán hình học và Vật lý? Chu kỳ của hàm số là một khái niệm, nội dung kiến thức quan trọng trong toán học và có ứng dụng rộng rãi trong nhiều lĩnh vực khác nhau. Đặc biệt là trong Toán Đại số và Giải tích 11.

Trong bài viết này, thayphu sẽ định nghĩa chu kỳ, giới thiệu các công thức của chu kì, phương pháp và bài tập của nó.

Định nghĩa của chu kì hàm số

• Chu kỳ của hàm số là khoảng cách giữa hai điểm đồng nhất trên đồ thị của hàm số. Nó thường được đo bằng đơn vị độ dài trên trục x. Chu kỳ cho phép chúng ta xác định sự lặp lại và các mô hình tuần hoàn trong hàm số.
• Hàm số f được gọi là hàm số tuần hoàn nếu với hằng số P (khác 0), ta có phương trình: f(x+P)=f(x), với điều kiện là mọi x đều ở trong miền xác định. Thì khi đó, có thể nói hằng số P (khác 0) được xem là chu kỳ của hàm số đó. Nếu có ít nhất một hằng số P có tính chất này thì ta gọi là chu kỳ cơ sở (chu kỳ gốc).

Tính chất

Chúng ta đã hiểu định nghĩa cụ thể của hàm tuần hoàn, hãy cùng ôn lại một số tính chất cơ bản của hàm tuần hoàn và cách nhận biết chúng:

• Nếu hàm f là hàm số tuần hoàn của chu kỳ P thì với mọi số x và mọi số nguyên n trong tập xác định của f, vậy ta có:

f(x+nP)=f(x)

• Nếu f(x) là hàm số tuần hoàn có chu kỳ P thì f(ax) với a là số thực khác 0, là hàm tuần hoàn có chu kỳ là P/|a|

Ví dụ: hàm số f(x)=cos(x) có chu kỳ 2 thì cos(9x) sẽ có chu kỳ là 2/9

Cách tìm chu kỳ của hàm số lượng giác (nếu có):

Phương pháp giải các dạng bài về chu kì của hàm số

Phương pháp 1: Chứng minh hàm số y = f(x) tuần hoàn

• Bước 1: Xét hàm số y = f(x) thuộc miền xác định D, ta cần dự đoán số thực dương T0, sao cho với mọi x ∈ D, ta có: x - T0 và x + T0 ∈ D (1); f(x +T0)=f(x) (2).
• Bước 2: Chúng ta kết luận rằng hàm số y=f(x) là hàm số tuần hoàn.

Phương pháp 2: Chứng minh T0 là chu kì của hàm số

Điều này có nghĩa là ta cần chứng minh T0 là số nhỏ nhất (1), (2) và ta chứng minh bằng phản chứng.

• Bước 1: Giả sử số T sao cho 0 < T < T0 thỏa mãn tính chất (2): x∈D, f(x + T) = f(x) ⇔ …⇒ mâu thuẫn với giả định 0 < T < T0 .
• Bước 2: Khi mâu thuẫn này xảy ra, chứng minh T0 là số dương nhỏ nhất thỏa mãn (2).
• Bước 3: Do đó ta có thể kết luận hàm số y = f(x) là hàm tuần hoàn có chu kỳ cơ sở T0.

Phương pháp 3: Xét tính tuần hoàn của hàm số lượng

Chu kì của hàm y = sinx và y = cosx là 2π

Với hàm y = sin(ax + b) và y = cos(ax + b), điều kiện: a ≠ 0, chu kỳ: 2π/a.

Chu kỳ của hàm y = tanx và y = cotx là π

Với hàm y = tan(ax + b) và y = cot(ax + b), điều kiện: a ≠ 0, chu kỳ: π/a.

Bài tập

Bài tập 1: Tìm chu kì tuần hoàn của hàm số

1. y=2sin2x.sin4x

Gợi ý lời giải:

Ta có: y=2sin2x.sin4x=cos6x+cos2x

Chu kì của hàm số y=cos6x là T1=2/6=/3

Chu kì của hàm số y=cos2x là T2=2/2=

Vậy chu kì của hàm số y=2sin2x.sin4x là T=

2. y=cos2x+sinx2.

Gợi ý lời giải:

Ta có:

y=f1(x)=cos2x T1=22=

y=f2(x)=sinx2 T2=21/2=4

Từ đó suy ra y=f(x)=f1(x)+f2(x) T là bội chung nhỏ nhất của (T1,T2).

Bài tập 2: Cho bảng biến thiên của hàm số y=f(x) như sau, hãy tìm khoảng đồng biến của hàm số là khoảng nào?

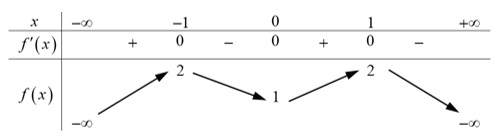
Gợi ý lời giải:

Dựa vào bảng biến thiên đã cho của hàm số y=f(x) đồng biến trên các khoảng (-;-1) và (-1;0).

Vậy hàm số đã cho đồng biến trên khoảng (-1;0).

Bài tập 3: Tìm giá trị lớn nhất, nhỏ nhất của hàm số -1cos3x1

Gợi ý lời giải:

Với mọi x ta có: -1cos3x1 nên 0 cos3x1

0-2cos3x-2

11-2cos3x-1 1y-1

Vậy M=1, m=-1.

Trên đây là định nghĩa, tính chất và những phương pháp giải cho các dạng toán chu kì của hàm số. Bằng cách xác định tính tuần hoàn, tìm chu kỳ và áp dụng chúng vào các bài toán cụ thể, chúng ta có thể giải quyết các bài toán liên quan đến tính tuần hoàn của hàm số.

Hy vọng rẳng bài viết này của thayphu.net đã cung cấp cho bạn những thông tin hữu ích và giúp bạn nắm bắt được cách giải quyết các bài toán liên quan.