Phép nhân hai số nguyên cùng dấu: Định nghĩa, tính chất, quy tắc

Thế nào là phép nhân hai số nguyên cùng dấu? Định nghĩa, tính chất, quy tắc thực hiện cụ thể phép nhân số nguyên cùng dấu.

Phép nhân hai số nguyên cùng dấu được thực hiện bằng cách nhân các giá trị tuyệt đối của hai số. Khi nhân hai số nguyên có cùng dấu, kết quả luôn là một số dương. Đây là một dạng toán tuy cơ bản nhưng rất quan trọng trong chương trình toán lớp 6, bởi nó là kiến thức nền tảng để giải nhiều dạng toán khác.

Trong bài viết này, hãy cùng thayphu tìm hiểu về kiến thức của phép nhân hai số nguyên cùng dấu như định nghĩa, tính chất, cách thực hiện và ứng dụng của chúng. Ngoài ra còn có các dạng bài tập vận dụng từ đơn giản đến nâng cao để các bạn học sinh có thể luyện tập thêm.

Phép nhân hai số nguyên cùng dấu là gì?

Phép nhân hai số nguyên cùng dấu là phép toán nhân hai số nguyên có cùng dấu, tức là cả hai số đều là số dương hoặc cả hai số đều là số âm. Khi hai số nguyên cùng dấu được nhân với nhau, kết quả luôn là một số dương.

Ví dụ:

(-3).(-9) = 27

5.6 = 30

(-2).(-8) = 16

Tính chất của phép nhân số nguyên

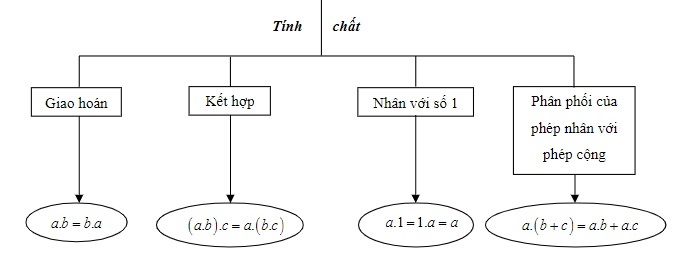
• Giao hoán: ∀a, b ∈ Z: a.b = b.a
• Kết hợp: ∀a,b, c ∈ Z: (a.b).c = a.(b.c)
• Nhân với số 1: ∀a ∈ Z :a.1 = 1.a = a
• Tính chất phân phối của phép nhân với phép cộng (và phép trừ):
• ∀a, b, c ∈ Z: a.(b + c) = a.b + a.c
• ∀a, b, c ∈ Z: a.(b − c) = a.b − a.c
• Tích một số chẵn các thừa số nguyên âm sẽ mang dấu "+”.
• Tích một số lẻ các thừa số nguyên âm sẽ mang dấu “−”.

Ví dụ:

• Giao hoán: 2.(-3) = (-3).2 = -6
• Kết hợp: [9.(-5)].2 = 9.[(-5).2] = 9.(-10) = -90
• Nhân với số 1: 7.1 = 1.7 = 7
• Phân phối: 2.(3 + 4) = 2.3 + 2.4

Cách thực hiện phép nhân hai số nguyên cùng dấu

Quy tắc: Muốn nhân hai số nguyên cùng dấu, ta nhân hai giá trị của chúng rồi đặt dấu “+” trước kết quả của chúng.

Các bước thực hiện cụ thể:

• Bước 1: Xác định hai số nguyên cùng dấu cần tính.
• Bước 2: Lấy giá trị tuyệt đối của hai số đó (bỏ qua dấu âm). Điều này không ảnh hưởng đến kết quả cuối cùng, vì khi nhân hai số nguyên cùng dấu, kết quả luôn là số dương.
• Bước 3: Nhân hai giá trị tuyệt đối đã lấy được trong bước trước.
• Bước 4: Kết quả của phép nhân chính là kết quả cuối cùng. Ta không cần thay đổi dấu, vì phép nhân hai số nguyên cùng dấu sẽ luôn cho kết quả dương.

Ví dụ: (-3) x (-4)

Ta thấy hai số nguyên có cùng dấu âm là -3 và -4.

Lấy giá trị tuyệt đối của hai số: |(-3)| = 3 và |(-4)| = 4.

Nhân hai giá trị tuyệt đối đã lấy: 3 x 4 = 12.

Vậy (-3) x (-4) = 12.

Cách nhận biết dấu của tích:

(+).(+)→(+)

(+).(−)→(−)

(−).(+)→(−)

(−).(−)→(+)

Ứng dụng của phép nhân hai số nguyên

• Tính diện tích: Trong hình học, phép nhân hai số nguyên cùng dấu được sử dụng để tính diện tích các hình học đơn giản như hình vuông, hình chữ nhật, tam giác. Ví dụ, khi có một hình vuông có cạnh dương a, diện tích của nó là a x a = a^2. Tương tự, diện tích của một hình chữ nhật có chiều dài dương a và chiều rộng dương b là a x b.
• Tính tổng giá trị: Phép nhân hai số nguyên cùng dấu cũng được sử dụng để tính tổng giá trị của các mặt hàng trong các danh sách, bảng biểu và các ứng dụng tài chính. Ví dụ, trong một danh sách các mặt hàng có số lượng dương và giá tiền dương, ta có thể sử dụng phép nhân này để tính tổng giá trị của các mặt hàng đó.
• Tính toán vật lý và kỹ thuật: Trong lĩnh vực khoa học và kỹ thuật, phép nhân hai số nguyên cùng dấu được sử dụng để tính toán các đại lượng vật lý và kỹ thuật. Ví dụ, trong công thức tính công suất, công thức tính điện trở, công thức tính tốc độ, ta thường sử dụng phép nhân hai số nguyên cùng dấu để tính toán các giá trị tương ứng.
• Ứng dụng trong tài liệu và báo cáo: Trong việc trình bày dữ liệu và báo cáo, phép nhân hai số nguyên cùng dấu có thể được sử dụng để tính toán các giá trị và kết quả liên quan. Ví dụ, trong các báo cáo thống kê và tài liệu khoa học, phép nhân được sử dụng để tính toán các chỉ số và mô tả dữ liệu.

Bài tập vận dụng

Câu 1: Chọn khẳng định đúng trong các khẳng định sau đây:

1. Nếu a.b > 0 thì a và b là hai số nguyên dương
2. Nếu a.b > 0 thì a và b là hai số nguyên âm
3. Nếu a.b = 0 thì a = 0 và b = 0
4. Nếu a.b < 0 thì a và b là hai số nguyên khác dấu

Đáp án: D

Giải thích:

Nếu a.b > 0 thì a và b là hai số nguyên cùng dấu, tức a và b có thể cùng là số nguyên âm hoặc cùng là số nguyên dương. Vậy đáp án A và B sai.

Nếu a.b = 0 thì a = 0 hoặc b = 0 . Vậy đáp án C sai.

Nếu a.b < 0 thì a và b là hai số nguyên khác dấu. Đáp án D đúng.

Câu 2: Kết quả của biểu thức (-34).(-8) là:

1. 272
2. -272
3. -26
4. 42

Đáp án: A

Câu 3: Hãy chọn biểu thức đúng trong các biểu thức dưới đây:

1. (-10).(-2) = -20
2. (-17).(-12) = 204
3. (-25).4 = 100
4. 11.(-11) = -1111

Đáp án: B

Câu 4: Hãy chọn mệnh đề sai trong các mệnh đề sau:

1. (-34).(-3) > 0
2. 4.(-121) < 0
3. (-40).11 < -500
4. 12.12 > 0

Đáp án: C

Câu 5: Tính giá trị của biểu thức sau: P = (-7)x + (-5)y = 0 với x = -5 và y = -9

1. P = -80
2. P = 10
3. P = -10
4. P = 80

Đáp án: D

Câu 6: Tính giá trị biểu thức sau: (36 - 16).(-5) + 6.(-14 - 6):

1. -220
2. 220
3. -20
4. 20

Đáp án: A

Trong bài viết này, thayphu.net đã cùng các bạn tìm hiểu về phép nhân hai số nguyên cùng dấu, cách thực hiện phép tính cũng như là một số ứng dụng của nó. Phép nhân này là một phép toán tuy cơ bản nhưng quan trọng và thường xuất hiện trong các đề thi cuối kì. Với việc nắm vững các quy tắc và luyện tập thường xuyên, các bạn sẽ có thể tăng tốc độ giải bài tập cũng như có thể tránh xảy ra sai sót trong việc tính toán hơn đấy.

Vì vậy hãy luyện tập các bài tập về dạng toán này từ cơ bản đến nâng cao để có thể hiểu rõ và nắm vững được dạng toán này nhé.