Tính chất chia hết cho một hiệu, chứng minh và bài tập áp dụng

Tính chất chia hết của một hiệu được phát biểu rằng nếu a chia hết cho (b - c) và b, thì a cũng chia hết cho c. Định nghĩa ví dụ minh họa và bài tập áp dụng.

Chia cho một hiệu là một quy tắc toán học mô tả mối quan hệ giữa một số nguyên chia cho một số hoặc hiệu giữa hai số khác nhau. Một cách đơn giản để hiểu phép chia cho hiệu là nếu một số nguyên chia hết cho cả hai số trong hiệu thì số đó cũng chia hết cho hiệu đó. Tính chất này có thể được sử dụng để giải các bài toán liên quan đến giải tích số, đại số, lý thuyết đồng dạng và nhiều lĩnh vực khác của toán học. Nó cung cấp cho chúng ta một cách hợp lý và có trật tự để tìm hiểu và hiểu sâu về bản chất và tính chất của số nguyên cũng như các phép toán liên quan.

Trong bài viết này của thayphu chúng ta sẽ tìm hiểu về định nghĩa cách chứng minh và bài tập áp dụng giúp các bạn học sinh dễ dàng nắm bắt tình chất này.

Định nghĩa về tính chia hết cho một hiệu

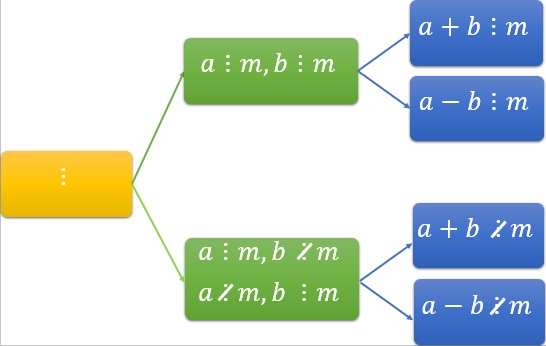
Định nghĩa ví dụ minh họa và bài tập áp dụng

Tính chia hết là một quy tắc toán học xác định xem một số tiền có thể chia được cho một số khác hay không. Để hiểu tính chất này, chúng ta cần biết hai định nghĩa quan trọng sau:

Tính chia hết

Số a được gọi là chia hết cho số b nếu có số nguyên dương k đại diện cho số a (trong đó b khác 0 ). = b×k. Trong trường hợp này, chúng ta cũng nói rằng b là thương của a và a là bội của b.

Tổng

Tổng là kết quả của việc cộng các số. Chúng ta có thể có tổng các số trong một dãy, tổng các số thực hoặc tổng các phần tử.

Thuộc tính thương nói rằng nếu một số nguyên chia hết cho một số khác thì tổng của các số đó cũng chia hết cho số đó. Điều này có thể được biểu diễn như sau:

Cho a, b và c là các số nguyên và a chia hết cho b và c, nghĩa là a chia hết cho b và a chia hết cho c.

Bây giờ chúng ta có tính chất: a + a + ... + a (n lần) chia cho b và c.

Tính chất chia hết của một hiệu

Để hiểu tính chất này, giả sử có ba số nguyên a, b và c. Nếu một số chia hết cho

b (b - c), thì chúng ta có thể xác minh rằng a cũng chia hết cho c.

Trường hợp này có thể biểu diễn bằng toán học như sau: Nếu a chia hết cho b (b - c) thì a cũng có thể chia hết cho c.

Ví dụ: Nếu biết số nguyên a chia hết cho 6 và 4, chúng ta có thể chứng minh rằng a cũng chia hết cho hiệu 6 - 4 = 2.

Chứng minh tính chất chia hết của một hiệu

Chứng minh tính chia hết của một hiệu

Để chứng minh tính chất của một hiệu, ta phải sử dụng phương pháp chứng minh dựa trên định nghĩa về tính chất chia hết của một hiệu

Giả sử a chia hết cho b và (b - c), ta cần chứng minh a cũng chia hết cho c.

Nếu a chia hết cho b thì theo định nghĩa tồn tại một số nguyên k sao cho a = b * k.

Tương tự, nếu a với (b - c) thì tồn tại số nguyên m sao cho a = (b - c) * m.

Để chứng minh a chia hết cho c, ta cần chứng minh c chia hết cho a, tức là a chia hết cho c.

Ta có:

a = b * k (từ việc a chia cho b)

a = (b - c) * m (từ việc a chia cho (b - c)

Từ hai biểu thức trên ta có thể trừ khỏi phương trình:

b * k = (b - c) * m

Khai triển biểu thức ta được:

b * k = b * m - c * m

Điều này giống như: b * k + c * m = b * m

Ta có thể viết dưới dạng: b * k + c * m - b * m = 0

Rút gọn biểu thức: b * (k - m) + c * m = 0

Vì m đều là số nguyên nên chúng ta có thể xác minh rằng (k - m) và m đều chia hết cho b.

Nghĩa là c chia hết cho b cho nên a được chia cho c.

Một số dạng toán về tính chia hết cho một hiệu

Sau khi bạn đã hiểu về định nghĩa cũng như các tính chất dưới đây thayphu đã tổng hợp những dạng toán về tính chất chia hết của một hiệu mà bạn có thể tham khảo:

Chứng minh rằng a chia hết cho b và c chia hết cho d

Bạn cần chứng minh rằng a - c khác với b - d.

Ví dụ: Cho biết 15 chia hết cho 3 và 9 chia hết cho 6. Chứng minh rằng 15 - 9 chia hết cho 3 - 6.

Giải: Ta biết 15 chia hết cho 3 và 9 chia hết cho 6. Vậy theo tính chất chia hết của một hiệu, ta có:

15 - 9 chia hết cho 3 - 6

6 chia hết cho -3

Vì -3 là một ước của 6, nên ta kết luận được rằng 6 chia hết cho -3.

Chứng minh rằng a chia hết cho b và c chia hết cho d

Ta chứng minh rằng a + c khác với b + d.

Ví dụ: Cho biết 20 chia hết cho 5 và 15 chia hết cho 3. Chứng minh rằng 20 + 15 chia hết cho 5 + 3.

Giải: Ta biết 20 chia hết cho 5 và 15 chia hết cho 3. Vậy theo tính chất chia hết của một hiệu, ta có:

20 + 15 chia hết cho 5 + 3

35 chia hết cho 8

Vì 8 là một ước của 35, nên ta kết luận được rằng 35 chia hết cho 8.

Chứng minh rằng a chia hết cho b và a chia hết cho c

Chúng ta chứng minh rằng a có thể chia hết cho b - c.

Ví dụ 3: Cho biết 12 chia hết cho 4 và 12 chia hết cho 6. Chứng minh rằng 12 chia hết cho 4 - 6.

Giải: Ta biết 12 chia hết cho 4 và 12 chia hết cho 6. Vậy theo tính chất chia hết của một hiệu, ta có:

12 chia hết cho 4 - 6

12 chia hết cho -2

Vì -2 là một ước của 12, nên ta kết luận được rằng 12 chia hết cho -2.

Bài tập áp dụng

Bài tập 1: Chứng minh rằng nếu a chia hết cho b và c chia hết cho d, thì a - c chia hết cho b - d.

Đáp án: Giả sử a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Tương tự, vì c chia hết cho d, tồn tại số nguyên m sao cho c = md.

Khi đó, a - c = kb - md = (k - m)d + (b - d).

Vì (k - m) và (b - d) đều là số nguyên, ta có a - c chia hết cho b - d.

Bài tập 2: Chứng minh rằng nếu a chia hết cho b, thì mọi bội số của a cũng chia hết cho b.

Đáp án : Vì a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Giả sử n là một bội số của a, tức là tồn tại số nguyên t sao cho n = at.

Thay vào giá trị của a, ta có n = (kb)t = k(bt).

Vì k và t đều là số nguyên, n chia hết cho b.

Bài tập 3: Chứng minh rằng nếu a chia hết cho b và a chia hết cho c, thì a chia hết cho bội chung nhỏ nhất của b và c.

Đáp án : Vì a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Tương tự, vì a chia hết cho c, tồn tại số nguyên m sao cho a = mc.

Đặt d là bội chung nhỏ nhất của b và c.

Khi đó, d chia hết cho b và d chia hết cho c.

Sử dụng tính chất truyền của chia hết, ta có d chia hết cho a.

Do đó, a chia hết cho d.

Bài tập 4: Chứng minh rằng nếu a chia hết cho b và b chia hết cho c, thì a chia hết cho c.

Đáp án 4: Vì a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Tương tự, vì b chia hết cho c, tồn tại số nguyên m sao cho b = mc.

Thay vào giá trị của b, ta có a = k(mc) = (km)c.

Vì km là một số nguyên, a chia hết cho c.

Bài tập 5: Chứng minh rằng nếu a chia hết cho b và a chia hết cho c, thì a chia hết cho bội chung nhỏ nhất của b và c.

Đáp án: Vì a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Tương tự, vì a chia hết cho c, tồn tại số nguyên m sao cho a = mc.

Đặt d là bội chung nhỏ nhất của b và c.

Khi đó, d chia hết cho b và d chia hết cho c.

Sử dụng tính chất truyền của chia hết, ta có d chia hết cho a.

Do đó, a chia hết cho d.

Bài tập 6: Chứng minh rằng nếu a chia hết cho b và b không chia hết cho c, thì a không chia hết cho c.

Đáp án: Giả sử a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Vì b không chia hết cho c, ta có thể viết b = mc + r, trong đó m và r lần lượt là phần nguyên và phần dư của phép chia b cho c, với 0 ≤ r < c.

Thay vào giá trị của b, ta có a = k(mc + r) = (km)c + kr.

Vì kr là một số nguyên và (km)c là bội của c, a chia hết cho c khi và chỉ khi kr chia hết cho c.

Vì r < c, nên kr không chia hết cho c.

Do đó, a không chia hết cho c.

Bài tập 7: Chứng minh rằng nếu a chia hết cho b và b chia hết cho a, thì |a| = |b|.

Đáp án: Vì a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Tương tự, vì b chia hết cho a, tồn tại số nguyên m sao cho b = ma.

Thay vào giá trị của b, ta có kb = ma.

Chia cả hai vế của phương trình trên cho ab (với a và b khác 0), ta được k/a = m/b, hay k = ma/b.

Vì a, b, k, m đều là số nguyên và a/b = k/m, nên ta có a = kb = m(a/b) = ma.

Từ đó suy ra |a| = |b|.

Bài tập 8: Chứng minh rằng nếu a chia hết cho b và b chia hết cho c, thì a chia hết cho c.

Đáp án: Vì a chia hết cho b, tức là tồn tại số nguyên k sao cho a = kb.

Tương tự, vì b chia hết cho c, tồn tại số nguyên m sao cho b = mc.

Thay vào giá trị của b, ta có a = k(mc) = (km)c.

Vì km là một số nguyên, a chia hết cho c.

Thayphu.net hy vọng qua bài viết này các bạn hiểu được kiến thức cơ bản của tính chất chia hết của hiệu và có thể vận dụng chúng để giải các bài toán thực tế. Đồng thời, những thông tin này sẽ là cơ sở cho những nghiên cứu sâu hơn về lĩnh vực này trong tương lai.

Tính chất chia hết cho hiệu là một khía cạnh quan trọng của toán học. Việc hiểu và áp dụng các tính chất này không chỉ giúp chúng ta giải các bài toán chia một cách hiệu quả mà còn cung cấp nền tảng cho việc học các bài toán phức tạp hơn trong toán học và logic.