Tập hợp con là gì? ký hiệu, tính chất và bài tập về tập hợp con

Tập hợp con là kiến thức quan trọng trong chương trình toán lớp 6. Bài viết sau, Thayphu sẽ chia sẻ cho các bạn học sinh về tập hợp con và những bài tập liên quan.

Như các bạn đã được học, tập hợp chính là khái niệm cơ bản của toán học, tuy nhiên trong cuộc sống, người ta vẫn thường hay nói về thuật ngữ này. Ví dụ như tập hợp những số tự nhiên bé hơn 5, hoặc tập hợp các bạn học sinh khối 6,... Trong các kiến thức về tập hợp có một nội dung lục cùng quan trọng, đó là tập hợp con.

Bài viết sau đây của Thayphu sẽ tổng hợp tất cả kiến thức và bài tập liên quan đến nội dung này.

Khái niệm tập hợp con

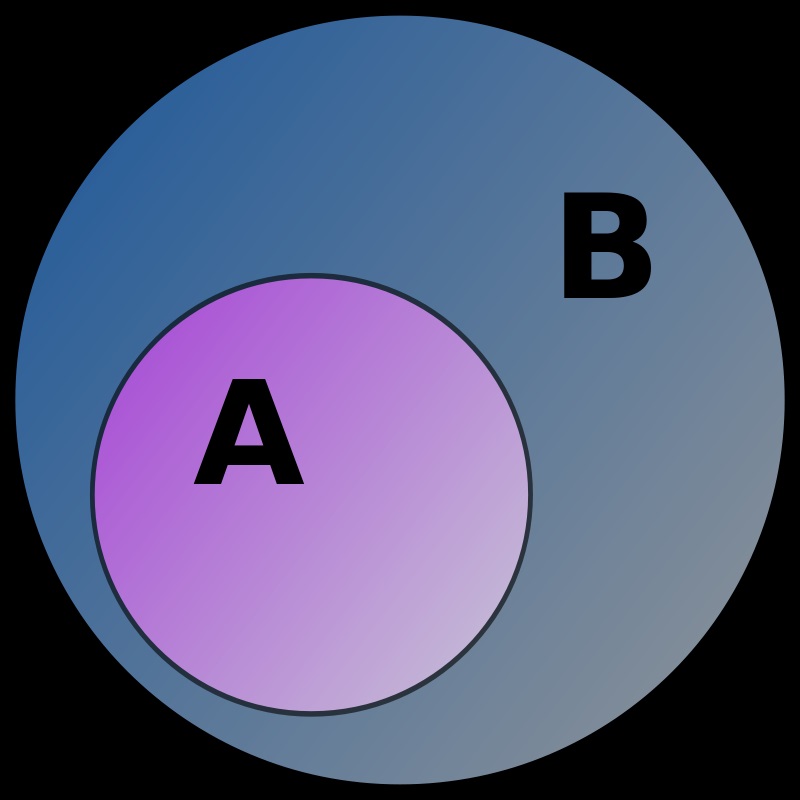
Tập A được xem là tập con của tập B

Như đã được đề cập, trong toán học và cả trong đời sống, chúng ta rất thường xuyên sử dụng khái niệm tập hợp. Tập hợp các thẻ anime Harry Potter, tập hợp các bạn tình nguyện viên lớp 6A, tập hợp những con số từ 1 đến 100…

Đối với toán học, người ta sẽ dùng chữ cái in hoa để đặt tên cho tập hợp, dùng chữ cái thường để đặt tên cho các phần tử trong một tập hợp. Một tập hợp sẽ bao gồm một phần tử, nhiều phần tử, lục số phần tử hoặc thậm chí là không có phần tử nào. Và khi các phần tử trong một tập hợp đứng riêng ra thành một tập hợp mới, người ta gọi là tập hợp con.

Định nghĩa tập hợp con: Với A là một tập hợp bất kỳ, tập B được gọi là tập hợp con của tập A nếu như các phần tử của tập B đều nằm trong tập A.

Kí hiệu, cách đọc và cách quy ước về tập hợp con

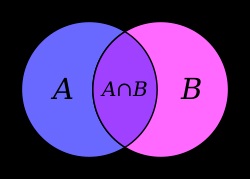
Phần chung của hai tập hợp A và B cũng được gọi là tập con

Nếu như các phần tử nằm trong tập hợp A đều thuộc tập hợp B, khi đó toán học xuất hiện quy ước tập hợp A là tập hợp con của tập hợp B. Hay nói theo một cách khác, tập hợp B chứa tập hợp A, còn tập hợp A được chứa bởi tập hợp B. Ký hiệu là A ⊂ B (hoặc B ⊃ A).

Trong trường hợp cả hai tập hợp A và B có cùng chung các phần tử, thì tập hợp A và tập hợp B đồng thời là tập con của nhau. Khi đó, tập hợp A bằng tập hợp B, kí hiệu là A = B.

Quy ước: Bất kỳ tập hợp nào cũng có 1 tập con là tập rỗng, hay nói cách khác tập rỗng là tập con của mọi tập hợp.

Cách đếm tập hợp con: Xét một tập A gồm có n phần tử, thì tổng số tập con của tập A là 2^n. Ví dụ, A có 5 phần tử, có nghĩa là A có 2⁵ = 32.

Một số tính chất của tập hợp con cần nhớ

Dựa vào những kiến thức cơ bản, chắc chắn các bạn có thể hiểu được rõ khái niệm, cũng như phân biệt được các ký hiệu trong một tập con. Sau đây, thayphu.net sẽ giới thiệu tiếp cho các bạn một số tính chất của tập hợp con cần phải nhớ đó là:

Ta có giả thuyết, tập A là tập hợp con của tập B thì khi đó:

• Tất cả các phần tử nằm trong tập A đều có ở trong tập B
• Số phần tử của tập B lớn hơn hoặc bằng tập A.
• Nếu như tập B là con của tập C, khi đó theo tính chất bắc cầu, A cũng là tập con của C.

Các loại bài tập về tập hợp con cơ bản

Câu hỏi và đáp án phần bài tập về tập hợp con

Các bài tập trắc nghiệm

Bài 1: Cho 2 tập hợp sau: A = {3; 4; 7}, B = {1; 2; 3; 4; 5; 7}. Chọn phương án đúng:

1. A ⊂ B
2. B ⊂ A
3. A = B
4. A ∈ B

ĐÁP ÁN: A

Bài 2: Cho ba tập hợp A = {1; c; d}; B= {a; b; d; e}, C = {1; a; b; c; d; e}. Chọn phương án đúng:

1. B ⊂ A và C ⊂ A
2. A ∈ C và B ∈ C
3. A ⊂ C và B ⊂ C
4. A = B = C

ĐÁP ÁN: C

Bài 3: Gọi A là tập hợp số tự nhiên lớn hơn 5 nhỏ hơn 10, B là tập hợp số tự nhiên nhỏ hơn 8, Ν* là tập hợp số tự nhiên khác 0 . Chọn phương án đúng:

1. B ⊂ A
2. A ⊂ N*
3. B ⊂ N*
4. A ⊂ B

ĐÁP ÁN: B

Bài 4: Cho tập hợp M = {0; 1; 3; 5; 7}. Chọn phương án sai:

1. {0; 1} ⊂ M
2. 0 ⊂ M
3. 3 ∈ M
4. 6 ∉ M

ĐÁP ÁN: B (chính xác là: {0} ⊂ M)

Bài 5: Viết tập hợp con khác rỗng của tập hợp A = {1; 4; 7}

1. {1}, {1; 4}
2. {1}, {4}, {7}
3. {1}, {4}, {7}, {1; 4}, {1; 7}, {4; 7}
4. {1}, {4}, {7}, {1; 4}, {1; 7}, {4; 7}, {1; 4;7}

ĐÁP ÁN: D

Bài 6: Cho tập B = {a; b; c; d; 0}, tính số tập hợp con của tập B trên.

1. 5
2. 10
3. 25
4. 32

ĐÁP ÁN: D

Các bài tập tự luận

Bài 1: Hình vẽ dưới đây biểu thị mối quan hệ tập hợp các số trong toán học, điền dấu thích hợp vào chỗ chấm:

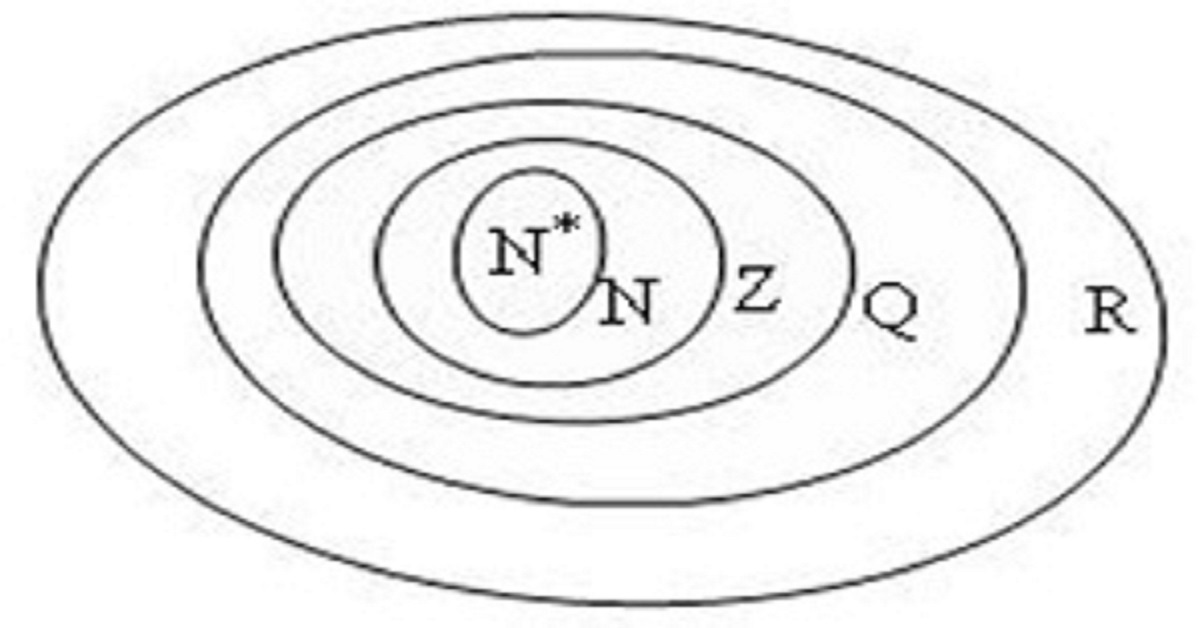
• N* … N
• N* … Q
• R … Z
• Q … N
• N* … Z … R

ĐÁP ÁN:

• N* ⊂ N
• N* ⊂ Q
• R ⊃ Z
• Q ⊃ N
• N* ⊂ Z ⊂ R

Bài 2: Cho tập hợp K = {đỏ; cam; vàng; lục; lam}.

a. Tập hợp K có mấy tập hợp con gồm 1 phần tử? Đó là những tập hợp nào?

b. Tập hợp K có mấy tập hợp con gồm 2 phần tử? Đó là những tập hợp nào?.

c. Tập hợp K có mấy tập hợp con gồm 3 phần tử? Đó là những tập hợp nào?

d. Tập rỗng có phải là tập hợp con của K hay không?

ĐÁP ÁN

a. Các tập hợp con có 1 phần tử của K là: {đỏ}; {cam}; {vàng}; {lục}; {lam} => có 5 tập con

b. Các tập hợp con có 2 phần tử của K là: {đỏ; cam}; {đỏ; vàng}; {đỏ; lục}; {đỏ; lam}; {cam; vàng}; {cam; lục}; {cam; lam}; {vàng; lục}; {vàng; lam}; {lục; lam} => có 10 tập con

c. Các tập hợp con có 3 phần tử của K là: {đỏ; cam; vàng}; {đỏ; cam; lục}; {đỏ; cam; lam}; {đỏ; vàng; lục}; {đỏ; vàng; lam}; {đỏ; lục; lam}; {cam; vàng; lam}; {cam; vàng; lục}; {vàng; lục; lam} => có 9 tập con.

d. Đúng vậy, tập rỗng là tập con của tập K.

Bài 3: Gọi tập M = {a; b; 2; 5}, tập N = {1; 2; 3; 4; 5}. Hãy viết tất cả các tập hợp là vừa tập con của M và N.

ĐÁP ÁN: Những tập hợp vừa là tập con của M vừa là tập con của N bao gồm: {2}; {5}; {2; 5}

Bài 4: Xét các trường hợp sau, trường hợp nào A là tập con của B?

a. A = {5; 8; 9}, B = {5; 7; 9}

b. A = {m; n}, B = {m; n; o}

ĐÁP ÁN

a. Trường hợp này A không phải là tập con của B.

b. Trường hợp này A chính là tập con của B.

Bài 5: Cho ba tập hợp X, Y, T sau đây, tập nào là tập con của tập còn lại. Hãy sử dụng kí hiệu để thể hiện một quan hệ tập hợp với tập N.

• X là tập hợp những số tự nhiên bé hơn 13
• Y là tập hợp số chẵn
• T là tập hợp số tự nhiên khác 13

ĐÁP ÁN

Ta có: X = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13}

Y = {2; 4; 6; 8; 10; 12 ….}

T= {a ∈ N / a ≠ 13}

Từ đó, ta có: X ⊂ T và Y ⊂ T

Quan hệ của ba tập hợp X, Y, T với tập N là: X ⊂ N; Y ⊂ N; T ⊂ N

Kết luận

Trên đây là toàn bộ nội dung chia sẻ cho các bạn học sinh về tập hợp con trong toán học. Hy vọng rằng, bài viết của thayphu.net mang lại cho bạn kiến thức bổ ích, giúp bạn nắm chắc nội dung liên quan đến tập hợp con. Chúc các bạn có thể làm trọn vẹn những dạng bài tập về tập hợp con thật chính xác nhé!