Số chính phương là gì? Cách tính số chính phương và bài tập

Một số chính phương hoàn hảo về cơ bản là chính phương của một số tự nhiên cụ thể. Để học và nhận biết số chính phương một cách dễ dàng.

Số chính phương (những số có căn bậc hai là số nguyên) từ lâu đã khơi dậy sự tò mò và quan tâm của các nhà toán học. Những tính chất đặc biệt và ứng dụng rộng rãi của chúng trong nhiều lĩnh vực khác nhau đã khiến nó trở thành một chủ đề thú vị và quan trọng. Từ những số đơn giản như 1, 4, 9 cho đến những số phức tạp hơn. Cùng thayphu tìm hiểu trong bài học dưới đây nhé.

Giới thiệu về số chính phương

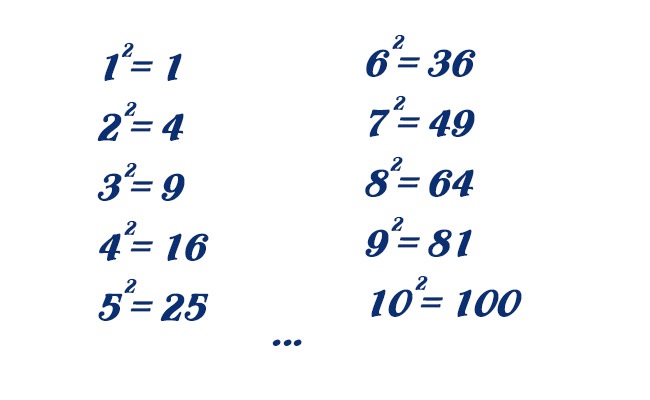
Số chính phương là gì trong toán học

Số chính phương là số có căn bậc hai là số nguyên. Điều này có nghĩa nó là kết quả của việc nhân một số nguyên với chính nó. Ví dụ: 1, 4, 9, 16, 25 và 36 là những số chính phương vì căn bậc hai của chúng là 1, 2, 3, 4, 5 và 6, tất cả đều là số nguyên.

Chúng là một phần quan trọng của toán học và được sử dụng rộng rãi trong nhiều lĩnh vực khác nhau.Việc nhận diện và nghiên cứu nó giúp chúng ta hiểu rõ hơn về cấu trúc của số tự nhiên và mối tương quan giữa chúng.

Nó không chỉ được tìm thấy trong toán học thuần túy mà còn được sử dụng trong các lĩnh vực khác như vật lý, công nghệ, mật mã và khoa học máy tính. Ví dụ, trong vật lý, số chính phương liên quan đến các khái niệm như tốc độ, gia tốc và năng lượng.

Trong công nghệ, các thuật toán mã hóa và bảo mật thông tin sử dụng chúng để tạo ra khóa bảo mật.

Tính chất của số chính phương

Số chính phương có những tính chất đặc biệt và quan trọng trong toán học. Dưới đây là một số tính chất cơ bản mà các bạn cần nắm.

Tính chất của căn bậc hai

Số chính phương là những số mà từ đó chúng ta nhận được một số nguyên bằng cách lấy căn bậc hai. Điều này có nghĩa là căn bậc hai của một số chính là số nguyên dương.

Tính chất của phép cộng

Tổng của hai số chính phương cũng là một số chính phương. Ví dụ: nếu a và b là số chính phương thì a + b cũng là nó. Điều này có thể được chứng minh bằng cách sử dụng tính chất căn bậc hai.

Tính chất của phép nhân

Tích của hai số chính phương cũng là một số chính phương.Ví dụ: nếu a và b là hình vuông thì a*b cũng là hình vuông.Điều này có thể được chứng minh bằng cách sử dụng tính chất căn bậc hai.

Tính chất lũy thừa

Nếu ta lấy một số chính phương lũy thừa lũy thừa của một số nguyên dương thì kết quả cũng là chúng. Ví dụ: nếu a là số chính phương và n là số nguyên dương thì a^n cũng là chính nó.

Liên hệ với dãy số

Số chính phương xuất hiện trong nhiều dãy số quan trọng như dãy số tự nhiên, dãy Fibonacci và dãy số Catalan. Chúng đóng một vai trò quan trọng trong việc nghiên cứu các mô hình và tính quy luật trong các dãy số này.

Cách nhận biết số chính phương

Để xác định một số có phải là số chính phương hay không, chúng ta có thể sử dụng các phương pháp nhận dạng sau:

Phương pháp căn bậc hai

Lấy căn bậc hai của số này. Nếu kết quả là số nguyên thì số ban đầu là số chính phương. Ví dụ:căn bậc hai của 9 là 3, là số nguyên nên 9 là số chính phương.

Phương pháp kiểm tra phép nhân

Kiểm tra xem số đó có phải là kết quả của phép nhân giữa hai số nguyên hay không. Ví dụ, để kiểm tra xem 16 có phải là số chính phương hay không, chúng ta có thể thử tìm hai số nguyên a và b sao cho a*b = 16. Trong trường hợp này chúng ta có 4*4 = 16, vậy 16 là số chính phương.

Phương pháp xác minh công thức

Một số chính phương có công thức tính toán đặc biệt.Ví dụ: từ 1 đến 100 có dạng 1^2, 2^2, 3^2, ..., 10^2. Nếu số có hình dạng này thì đó là số chính phương.

Sử dụng công cụ và thuật toán

Có các công cụ tính toán và thuật toán để kiểm tra xem một số có phải là số chính phương hay không. Ví dụ: có thể sử dụng thuật toán như “Kiểm tra xem một số có phải là số chính phương hay không bằng cách kiểm tra xem căn bậc hai của nó có phải là số nguyên hay không” có thể được sử dụng để đảm bảo độ chính xác và hiệu quả.

Cách tìm số chính phương

Cách tìm số chính phương

Để tìm số chính phương chúng ta có thể sử dụng các phương pháp sau:

Sử dụng căn bậc hai

Bắt đầu từ số 1, ta lấy căn bậc hai của các số tự nhiên lần lượt. Nếu kết quả là số nguyên thì số đó là số chính phương. Ví dụ: bằng cách lấy căn bậc hai của các số từ 1 đến 100, chúng ta tìm được các số chính phương từ 1 đến 10 (1, 4, 9, 16, 25, 36, 49, 64, 81, 100).

Kiểm tra bằng phép nhân

Bắt đầu từ số 1, ta kiểm tra xem có tồn tại hai số nguyên a và b sao cho a * b bằng số đang xét hay không. Nếu vậy thì số này là số chính phương. Ví dụ: để tìm số chính phương từ 1 đến 100, chúng ta kiểm tra phép nhân các cặp số nguyên (1*1, 2*2, 3*3,...), 10*10) và xác định các số tương ứng.

Sử dụng công thức

Một số chính phương có thể được tính bằng các công thức đặc biệt.Ví dụ: từ 1 đến 100 có dạng 1^2, 2^2, 3^2, ..., 10^2.

Sử dụng thuật toán

Có các thuật toán hiệu quả để tìm chúng trong một dãy số rộng.Một ví dụ là thuật toán “Kiểm tra xem một số có phải là số chính phương hay không bằng cách kiểm tra xem căn bậc hai của nó có phải là số nguyên hay không.” Thuật toán này có thể được áp dụng để tìm chúng trong dãy số lớn.

Bài tập áp dụng

Bài tập áp dụng

• Bài tập 1: Chứng minh số n = 2006^2 + 2005^2 + 2004^2 – 2003^2
• Bài tập 2: Chứng minh 1234567890
• Bài tập 3: Chứng minh: Với mọi số tự nhiên n thì A = n(n+1)(n+2)(n+3) + 1
• Bài tập 4:: Cho dãy số sau, số nào là số chính phương 9, 81, 790, 400, 121, 380, 2500, 441, 560
• Bài tập 5: Tìm số tự nhiên x sao cho những số dưới đây là số chính phương: A = x²+ 2x + 12.

Mong rằng những thông tin chúng tôi cung cấp ở trên hữu ích cho bạn. Số chính phương là một khái niệm quan trọng trong toán học và có ứng dụng trong nhiều lĩnh vực khác nhau. Việc nhận biết và tìm chúng có thể giúp chúng ta hiểu thêm về tính chất và cấu trúc của các số nguyên.Nếu bạn có bất kỳ câu hỏi hoặc yêu cầu nào khác, hãy để lại cho chúng tôi biết.Chúng tôi sẽ cố gắng hỗ trợ bạn trong việc tìm hiểu thêm về số chính phương hoặc các chủ đề toán học khác.