Phép chia là gì? Ví dụ minh họa về phép chia trong toán học

Phép chia là một phép toán cơ bản trong toán học, trong đó nó chia một số cho một số khác để tìm ra kết quả hoặc tỷ lệ giữa chúng.

Phép chia là một khái niệm cơ bản trong toán học, trong đó chúng ta chia một số thành phần thành những phần nhỏ hơn. Đây là một phép toán quan trọng và thông dụng trong cuộc sống hàng ngày, từ việc chia bánh mì thành những phần nhỏ hơn cho đến tính toán tỷ lệ cho đến phân phối hàng hóa. Hiểu và nắm vững phép chia là một kỹ năng toán học quan trọng giúp chúng ta giải quyết các vấn đề, tình huống thực tế một cách chính xác và hiệu quả.

Trong bài viết này, chúng ta sẽ cùng thayphu khám phá sâu hơn về phép chia, các quy tắc và thuật toán liên quan cũng như ứng dụng thực tế của chúng trong cuộc sống hàng ngày.

Định nghĩa về phép chia trong toán học

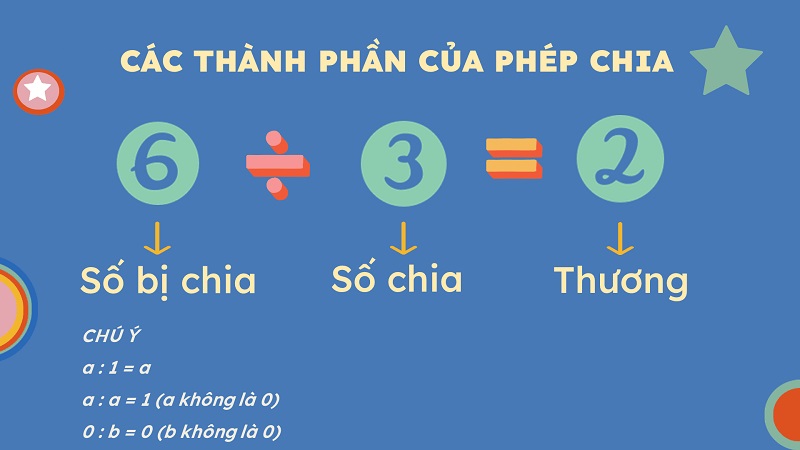
Định nghĩa về phép chia trong toán học

Phép chia là một phép toán chia một số cho một số khác để tìm kết quả hoặc tỉ số giữa chúng. Trong đó số chia gọi là số bị chia, số bị chia gọi là số chia và kết quả là thương. Nó có thể được áp dụng cho nhiều loại số khác nhau, bao gồm số nguyên, số thập phân và phân số. Khi chia, ta xác định số chia có thể chia cho số bị chia bao nhiêu lần. Với phép chia chính xác, kết quả là một số nguyên hoặc số thập phân chính xác.Nếu chúng không chia hết thì có phần nguyên và phần dư. Ví dụ: nếu chúng ta chia số 10 cho số 2 thì kết quả là 5 vì 2 * 5 = 10. Trong trường hợp này chúng ta có một phép chia chính xác và thương là một số nguyên. Tuy nhiên, nếu chúng ta chia số 10 cho số 3 thì kết quả sẽ là 3 số nguyên có số dư là 1, vì 3 * 3 + 1 = 10.Nó là một khái niệm quan trọng trong toán học và có nhiều ứng dụng trong đời sống hàng ngày, từ việc chia sẻ thức ăn, phân chia tài sản cho đến việc tính tỷ lệ. Hiểu và nắm vững phép chia là một kỹ năng cơ bản trong toán học.

Tính chất của phép chia

Nó có một số tính chất quan trọng mà bạn cần phải nắm rõ. Dưới đây là một số tính chất cơ bản của phép chia:

• Tính chất kết hợp: Phép chia có tính chất kết hợp, nghĩa là khi một số chia cho một số khác rồi chia cho một số khác thì kết quả cuối cùng không thay đổi. Ví dụ: (a `b) ` c = a ` (b × c).
• Tính chất giao hoán:Chúng có tính giao hoán, nghĩa là thứ tự của hai số khi chia sẽ ảnh hưởng đến kết quả. Ví dụ: a `b không bằng b `a trừ khi a = b.
• Tính chất phân phối: Phép chia có tính chất phân phối của phép nhân. Điều này có nghĩa là khi chúng ta chia tổng hoặc hiệu của hai số cho một số khác, chúng ta có thể chia từng số riêng lẻ rồi thực hiện phép chia cho từng thành phần rồi thực hiện phép nhân.Ví dụ: (a + b) ` c = (a ` c) + (b `c).
• Tính chất của số khi chia cho 0: Việc chia bất kỳ số nào cho 0 đều không được định nghĩa trong toán học. Điều này có nghĩa là không thể chia một số cho 0 để có kết quả hợp lệ. Khi chúng ta gặp phép chia cho 0, chúng ta nói rằng phép chia không tồn tại hoặc là vô hạn.
• Tính chất các số chia cho chính nó: Một số chia cho chính nó luôn bằng 1. Ví dụ: a ÷ a = 1.
• Tính chất của các số chia cho 1: Một số chia cho 1 luôn bằng 1 sẽ bằng con số này.Ví dụ: a ÷1 = a.

Dấu hiệu nhận biết phép chia

Nó là một phép toán trong toán học được sử dụng để chia một số (gọi là số bị chia) cho một số khác (gọi là số chia) để tìm ra kết quả (gọi là thương). Dấu hiệu nhận biết chúng bao gồm:

• Dấu chia (/): Dấu chia (/) được sử dụng để biểu thị phép chia. Ví dụ: 10 / 2 = 5.
• Dấu chia hết hoặc chia không hết: Khi số bị chia (số trong phép chia) chia hết cho số chia mà không có phần dư, ta nói số bị chia chia hết cho số chia. Ví dụ: 10 chia hết cho 2, ký hiệu là 10 chia 2 = 5. Ngược lại, nếu có phần dư, ta nói số bị chia không chia hết cho số chia. Ví dụ: 10 không chia hết cho 3, ký hiệu là 10 chia 3 = 3 dư 1.
• Thương và phần dư: Trong phép chia, thương là kết quả của phép chia và phần dư là số dư lại sau khi thực hiện phép chia. Ví dụ: 10 chia 3 = 3 dư 1, trong đó 3 là thương và 1 là phần dư.

Các dạng bài toán về phép chia thường gặp

Có rất nhiều dạng bài toán phép chia mà chúng ta thường gặp trong toán học và cuộc sống hàng ngày. Sau đây là một số dạng bài toán chia thường gặp: Bài toán chia đều: Trong loại bài toán này, chúng ta phải chia một đại lượng hoặc tính chất thành những phần bằng nhau. Ví dụ: Chia 24 quả táo vào 6 giỏ. Mỗi giỏ có bao nhiêu quả táo?

• Bài toán số nguyên: Trong loại bài toán này, chúng ta cần tìm một số nguyên khi biết tổng và phần dư của phép chia. Ví dụ: Tìm số nguyên khi chia 35 cho 7 dư 2.
• Bài toán tìm ước số: Ở dạng bài toán này, ta cần tìm ước số khi lấy tổng, thương và biết phần còn lại của phép chia. Ví dụ: Tìm ước số nếu biết tổng là 45, thương là 5 và số dư là 3.
• Bài toán tìm số dư: Ở dạng bài toán này ta cần tìm số dư của phép chia. Ví dụ: Tính số dư bằng cách chia 89 cho 6.
• Bài toán tỉ số: Ở dạng bài toán này ta phải tìm tỉ số giữa hai số để biết kết quả của phép chia.Ví dụ: Nếu chia 240 quả táo vào 12 giỏ thì mỗi giỏ có bao nhiêu quả táo?
• Bài toán ứng dụng thực tế: Phép chia còn được áp dụng cho các bài toán thực tế như chia tiền, chia bánh, chia thời gian và phân phối hàng hóa.

Một số lưu ý khi thực hiện phép chia

Dưới đây là một số lưu ý về phép chia:

• Đảm bảo số chia không bằng 0: Trước khi chia, hãy đảm bảo số chia không bằng 0. Chia một số cho 0 là số không xác định và không có giá trị hợp lệ.
• Xác định chính xác số chữ số thập phân: Khi chia cho số thập phân, hãy xác định chính xác số chữ số thập phân mà bạn muốn có trong kết quả. Điều này đảm bảo rằng kết quả là chính xác và đáp ứng được nhu cầu của bài toán.
• Làm tròn kết quả: Trong một số trường hợp, bạn có thể cần làm tròn kết quả phép chia để giảm số chữ số thập phân hoặc để đáp ứng nhu cầu của bài toán. Hãy chắc chắn rằng bạn hiểu quy tắc làm tròn và áp dụng nó một cách chính xác
• Xử lý phần dư: Nếu phép chia không chia hết thì phần dư có thể giữ nguyên. Phần còn lại có thể quan trọng đối với vấn đề hoặc có thể cần phải bỏ qua tùy theo nhu cầu của bạn.
• Kiểm tra kết quả: Sau khi chia, kiểm tra kết quả bằng cách nhân thương với số chia một lần nữa.Nếu kết quả của phép nhân không ra số ban đầu, hãy kiểm tra lại các thao tác chia để tìm lỗi.
• Sử dụng quy tắc, thuật toán phù hợp: Có rất nhiều quy tắc, thuật toán khác nhau để thực hiện phép chia. Sử dụng các quy tắc và thuật toán phù hợp với loại số và yêu cầu của bài toán để đưa ra kết quả chính xác và hiệu quả.

Bài tập áp dụng

Bài 1:48 ÷ 6 = ?

a) 6

b) 8

c) 12

d) 9

Đáp án: c) 12

Bài 2:75 ÷ 5 = ?

a) 10

b) 15

c) 8

d) 12

Đáp án: b) 15

Bài 3:144 ÷ 12 = ?

a) 12

b) 18

c) 16

d) 24

Đáp án: a) 12

Bài 4: 63 ÷ 7 = ?

a) 9

b) 7

c) 8

d) 6

Đáp án: a) 9

Bài 5:96 ÷ 4 = ?

a) 20

b) 24

c) 16

d) 12

Đáp án: b) 24

Bài 6:135 ÷ 9 = ?

a) 15

b) 12

c) 10

d) 17

Đáp án: a) 15

Bài 7:72 ÷ 8 = ?

a) 9

b) 6

c) 8

d) 12

Đáp án: c) 8

Bài 8: 147 ÷ 3 = ?

a) 45

b) 49

c) 51

d) 39

Đáp án: a) 49

Bài 9: 81 ÷ 9 = ?

a) 8

b) 7

c) 9

d) 6

Đáp án: c) 9

Bài 10:180 ÷ 6 = ?

a) 30

b) 20

c) 36

d) 15

Đáp án: a) 30

Bài 11:248 ÷ 4 = ?

a) 58

b) 64

c) 62

d) 56

Đáp án: b) 62

Bài 12: 312 ÷ 6 = ?

a) 52

b) 58

c) 42

d) 48

Đáp án: a) 52

Bài 13:432 ÷ 9 = ?

a) 38

b) 46

c) 48

d) 54

Đáp án: c) 48

Bài 14:525 ÷ 7 = ?

a) 70

b) 75

c) 80

d) 65

Đáp án: b) 75

Bài 15:648 ÷ 8 = ?

a) 76

b) 82

c) 72

d) 80

Đáp án: c) 72.

Trên đây là những thông tin chúng tôi đã giới thiệu đến bạn. Hy vọng rằng qua các lí thuyết và giải các bài tập này các em đã củng cố được kiến thức về phép chia. Phép chia là một khái niệm toán học quan trọng và được sử dụng rộng rãi trong nhiều lĩnh vực của đời sống hàng ngày cũng như trong các bài toán phức tạp hơn.