Công thức nhân hai lũy thừa cùng cơ số và bài tập áp dụng

Khi nhân hai lũy thừa cùng cơ số, ta giữ cơ số không đổi và cộng số mũ của hai lũy thừa với nhau. Định nghĩa, ứng dụng, công thức nhân hai lũy thừa cùng cơ số.

Lũy thừa cùng cơ số là một phép tính mà một số a được nhân với chính nó n lần, với số n lần này được biểu diễn bằng một số nguyên dương gọi là số mũ. Nhân hai lũy thừa cùng cơ số là một dạng toán cơ bản, quan trọng trong chương trình toán ở bậc trung học cơ sở, đặc biệt là toán đại số lớp 6, được áp dụng rộng rãi trong nhiều lĩnh vực khác nhau.

Trong bài viết này, thayphu sẽ cùng các bạn tìm hiểu về khái niệm thú vị này, như định nghĩa cơ bản, công thức tính và ứng dụng thú vị của nó. Ngoài ra, hãy cùng ôn tập lại bằng các dạng bài tập từ cơ bản đến nâng cao nhé.

Lũy thừa cùng cơ số là gì?

Lũy thừa cùng cơ số là một phép tính mà một số a được nhân với chính nó n lần, với số n lần này được biểu diễn bằng một số nguyên dương gọi là số mũ. Khi số mũ là một số tự nhiên (1, 2, 3, 4, ...), ta nói đó là lũy thừa với số mũ tự nhiên.

Nói cách khác, ta có thể hiểu đơn giản lũy thừa cùng cơ số là lũy thừa có dạng a^n. Trong đó, ta gọi a là cơ số và số mũ là n.

Công thức chung cho lũy thừa là:

a^n = a.a.a ... a (n lần).

Ví dụ: 7^5 = 7.7.7.7.7

Quy ước:

• a^1 = a, a^0 = 1.
• a^2 gọi là bình phương của số a.
• a^3 gọi là lập phương của số a.

Công thức nhân hai lũy thừa cùng cơ số

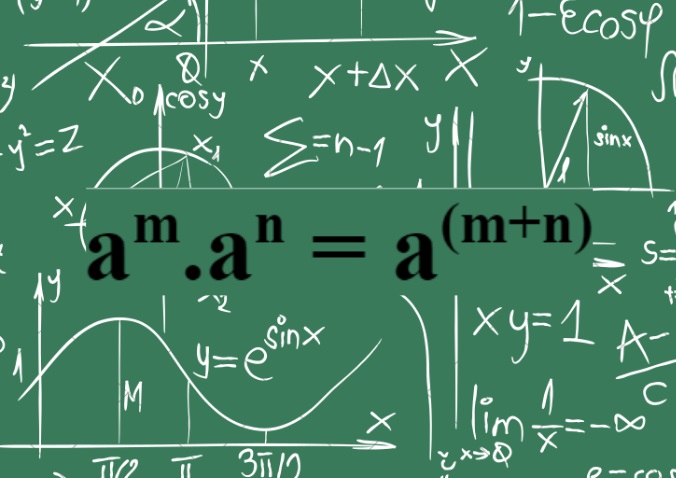
Khi nhân hai lũy thừa cùng cơ số, ta giữ cơ số không đổi và cộng số mũ của hai lũy thừa với nhau.

Công thức tổng quát:

a^m.a^n = a^(m+n)

Cách thực hiện nhân hai lũy thừa cùng cơ số:

• Xác định cơ số của lũy thừa.
• Giữ nguyên cơ số của hai lũy thừa và chỉ cộng hai số mũ của lũy thừa.
• Kết quả là lũy thừa mới với cùng cơ số và số mũ là tổng của phép tính đã tính.

Ví dụ: Thực hiện phép tính: 2^3.2^6

Ta có:

2^3 = 2.2.2

2^6 = 2.2.2.2.2.2

⇔ 2^3.2^6 = 2.2.2.2.2.2.2.2.2 = 2^(3+6) = 2^9

Ứng dụng của lũy thừa cùng cơ số

Tính toán tài chính: Trong lãi suất kép và quá trình tăng trưởng tài chính, nhân hai lũy thừa cùng cơ số được sử dụng để tính toán lợi nhuận và giá trị tương lai của đầu tư.

Mô hình hóa tăng trưởng: Trong các lĩnh vực như kinh tế, dân số học và sinh thái học, nhân hai lũy thừa cùng cơ số được sử dụng để mô hình hóa quá trình tăng trưởng và suy giảm.

Kỹ thuật và khoa học vật liệu: Trong một số lĩnh vực kỹ thuật và khoa học vật liệu, nhân hai lũy thừa cùng cơ số được sử dụng để tính toán và dự đoán sự thay đổi các thông số vật liệu theo thời gian.

Xử lý dữ liệu và tính toán số học: Trong lĩnh vực khoa học dữ liệu và tính toán số học, nhân hai lũy thừa cùng cơ số được sử dụng để thực hiện các phép tính nhanh chóng và đơn giản hóa các biểu thức phức tạp.

Mật mã học: Trong mật mã học, nhân hai lũy thừa cùng cơ số được sử dụng trong các thuật toán mã hóa và giải mã thông tin.

Bài tập vận dụng và ôn tập

Bài tập 1: Thực hiện các phép tính sau:

1. 2^7 . 2^6
2. 7^11 . 7^3
3. 3^2 . 3
4. 5^6 . 5^12

Gợi ý lời giải:

1. 2^7 . 2^6

= 2^(7 + 6) = 2^13

2. 7^11 . 7^3

= 7^(11 + 3) = 7^14

3. 3^2 . 3

= 3^(2 + 1) = 3^3

Hoặc phép toán đơn giản này t có thể nhẩm nhanh rằng 3.3.3 = 9.3 = 27.

4. 5^6 . 5^12

= 5^(6 + 12) = 5^18

Bài tập 2: Tìm x, biết:

1. 3^x = 1
2. x^4 = 1
3. 2^x = 16
4. x^2 = 9

Gợi ý lời giải:

1. 3^x = 1

Dựa vào quy ước của lũy thừa, ta có thể dễ dàng nhận ra:

3^x = 3^0 = 1 ⇒ x = 0

2. x^4 = 1

= 1^4 = 1 ⇒ x = 1

3. 2^x = 16

= 2^4 = 16 ⇒ x = 4

4. x^2 = 9

= 3^2 = 9 ⇒ x = 3

Bài tập 3: Chọn đáp án đúng trong các lựa chọn sau (bài tập trắc nghiệm ôn tập)

1. Tìm số tự nhiên n, biết rằng 5^n = 5^4 . 5^2

1. n = 4
2. n = 6
3. n = 8
4. n = 10

Đáp án: n = 6

2. Đâu là dạng lũy thừa của phép tính: 5.5.5.5

1. 5^2
2. 5^6
3. 5^3
4. 5^4

Đáp án: D

3. Đâu là dạng lũy thừa của 1 tỷ:

1. 10^5
2. 10^7
3. 10^9
4. 10^10

Đáp án: C. Ta có 1 tỷ = 1.000.000.000 = 10^9

Bài viết trên đã giới thiệu đến các bạn định nghĩa cơ bản của lũy thừa, công thức nhân hai lũy thừa cùng cơ số và ứng dụng của chúng trong cuộc sống.

Qua bài viết trên, thayphu.net mong rằng các bạn học sinh đã nắm rõ những kiến thức thú vị về nhân hai lũy thừa cùng cơ số. Đây là dạng toán tuy cơ bản nhưng là nền tảng quan trọng để xây dựng nên những kiến thức nâng cao ở các lớp lớn hơn. Vì vậy, các bạn hãy ôn tập thật kỹ và luyện tập giải bài tập thường xuyên để có thể nắm vững những kiến thức toán lớp 6 quan trọng này nhé.