Lũy thừa cùng cơ số gì? Cách xác định lũy thừa cùng cơ số

Lũy thừa cùng cơ số là lũy thừa nhân một số với một số cụ thể. Chúng ta sẽ tìm hiểu về quy tắc lũy thừa, tính chất của lũy thừa và cách áp dụng chúng trong các hệ thống cơ số khác nhau.

Trong thế giới toán học, một khái niệm cực kỳ quan trọng đã thu hút sự chú ý của những người đang tìm kiếm về toán học .Đó là lũy thừa cùng cơ số. Nó có vẻ là một khái niệm đơn giản, nhưng việc mở rộng và ứng dụng nó đã tạo ra những khám phá kỳ diệu và đặt nền móng vững chắc cho các lĩnh vực toán học và khoa học khác. Từ các công thức đơn giản đến các bài toán phức tạp, lũy thừa cùng cơ số mở ra cánh cửa dẫn đến một thế giới của sức mạnh và sự khám phá vô hạn.

Trong bài viết này hãy cùng thayphu khám phá lũy thừa cùng cơ số và ứng dụng của nó trong đời sống hằng ngày

Định nghĩa về lũy thừa cùng cơ số trong toán học

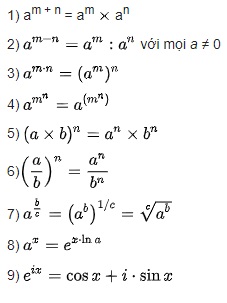
Định nghĩa về lũy thừa cùng cơ số trong toán học

Lũy thừa cùng cơ số là một khái niệm quan trọng trong toán học và mô tả quá trình nhân một số với một số cụ thể.

Nó được biểu diễn dưới dạng a^n, trong đó “a” là cơ số và “n” là số mũ. Khi tính lũy thừa, ta nhân cơ số “a” với chính nó “n” lần.

Ví dụ: nếu a = 2 và n = 3, ta viết 2^3 và tính như sau: 2^3 = 2 x 2 x 2 = 8. Đây là lũy thừa cơ số 2 có số mũ là 3.

Tính chất của lũy thừa cùng cơ số

Các lũy thừa cùng cơ số (còn gọi là lũy thừa) có một số tính chất quan trọng trong toán học.

Dưới đây là một số tính chất cơ bản của lũy thừa cùng cơ số:

• Tính chất nhân: a^m x a^n = a^(m+n). Điều này có nghĩa là khi nhân hai lũy thừa cùng cơ số, chúng ta có thể cộng các số mũ lại với nhau.
• Tính chất chia: a^m / a^n = a^(m-n). Nghĩa là, bằng cách chia hai lũy thừa cùng cơ số cho cùng một cơ số, chúng ta có thể trừ số mũ của chúng. Tính chất lũy thừa của mũ: (a^m)^n = a^(m*n). Nghĩa là, khi chúng ta nâng lũy thừa lên lũy thừa có cùng cơ số, chúng ta có thể nhân số mũ. Tính lũy thừa của số không âm: (a^m)^n = a^(m*n). Điều này chỉ áp dụng nếu cơ số “a” là số không âm.
• Tính lũy thừa của số 0: 0^n = 0.Nếu nâng số 0 lên lũy thừa dương thì kết quả luôn là 0. Tính lũy thừa của số 1: 1^n = 1. Nếu nâng số 1 lên lũy thừa của bất kỳ số mũ nào thì kết quả là luôn luôn 1.
• Thuộc tính lũy thừa của số âm: Nếu cơ số “a” là số âm và số mũ “n” là số nguyên dương lẻ thì kết quả là số âm (-a^n). Tuy nhiên, nếu số mũ “n” là số nguyên dương chẵn thì kết quả là số dương (a^n).
• Những tính chất này giúp chúng ta thực hiện các phép tính lũy thừa trên cùng một cơ sở một cách hiệu quả, linh hoạt và đóng vai trò quan trọng trong nhiều lĩnh vực toán học và khoa học tự nhiên.

Dấu hiệu nhận biết lũy thừa cùng cơ số

Dấu hiệu nhận biết lũy thừa cùng cơ số

Trong các biểu thức toán học có một số dấu hiệu xác định lũy thừa có cùng cơ số.

Dưới đây là một số ký tự phổ biến:

• Nó có cơ số và số mũ được phân tách bằng dấu mũ (^).

Ví dụ: a^n hoặc b^3 là cách biểu thị lũy thừa của cùng một số cơ sở.

• Có chỉ số mũ dương hoặc số mũ âm: Nếu số mũ là số nguyên dương hoặc số âm thì biểu thức có thể là lũy thừa của cùng một cơ số.

Ví dụ: a^2 hoặc b^-4 là các lũy thừa có cùng cơ số.

• Có một phép nhân hoặc phép chia trong biểu thức: Nếu có một phép nhân hoặc phép chia trong một biểu thức và một số được dùng làm số mũ thì đó có thể là lũy thừa có cùng cơ số.

Ví dụ: 2^3 x 5 hoặc (a^2) / (b^4).

Bài tập áp dụng

• Bài 1:Tính giá trị của 3^4.

Đáp án: 3^4 = 81.

• Bài 2:Tính giá trị của 2^(-3).

Đáp án: 2^(-3) = 1/8 = 0.125.

• Bài 3:Tính giá trị của (4^2)^3.

Đáp án: (4^2)^3 = 4^6 = 4096.

• Bài 4:Tính giá trị của 5^2 x 5^3.

Đáp án: 5^2 x 5^3 = 5^(2+3) = 5^5 = 3125.

• Bài 5:Tính giá trị của (2^3) / (2^2).

Đáp án: (2^3) / (2^2) = 2^(3-2) = 2^1 = 2.

• Bài 6:Tính giá trị của (6^2)^(-2).

Đáp án: (6^2)^(-2) = 6^(-4) = 1 / 6^4 = 1 / 1296 ≈ 0.00077.

• Bài 7: Tính giá trị của (9^0) x (7^3).

Đáp án: (9^0) x (7^3) = 1 x 7^3 = 7^3 = 343.

• Bài 8:Tính giá trị của (-2)^4.

Đáp án: (-2)^4 = 2^4 = 16.

• Bài 9:Tính giá trị của (-5)^3 x (-5)^2.

Đáp án: (-5)^3 x (-5)^2 = (-5)^(3+2) = (-5)^5 = -3125.

• Bài 10:Tính giá trị của (2^(-2))^(-3).

Đáp án: (2^(-2))^(-3) = 2^((-2) x (-3)) = 2^6 = 64.

Trên đây là một số bài tập về lũy thừa cùng cơ số từ đơn giản đến phức tạp, cùng với đáp án tương ứng. Hi vọng rằng những bài tập này đã giúp bạn làm quen và nắm vững khái niệm và các tính chất của lũy thừa cùng cơ số.