Dấu hiệu nhận biết số chính phương và bài tập áp dụng

Số chính phương là gì? Là số nguyên dương được biểu diễn dưới dạng bình phương của một số nguyên, tìm hiểu thêm tính chất và dấu hiệu nhận biết số chính phương.

Trên thế giới này có một loại số đặc biệt gọi là số phương. Những con số này có sức hấp dẫn đặc biệt và kích thích trí tò mò, khám phá của những người yêu thích toán học. Nó là số có thể biểu diễn dưới dạng bình phương của một số nguyên.

Hãy cùng thayphu khám phá thế giới kỳ diệu của những con số và những ứng dụng thú vị của chúng trong các lĩnh vực như toán học,vật lý, công nghệ và nhiều lĩnh vực khác.

Số chính phương là gì?

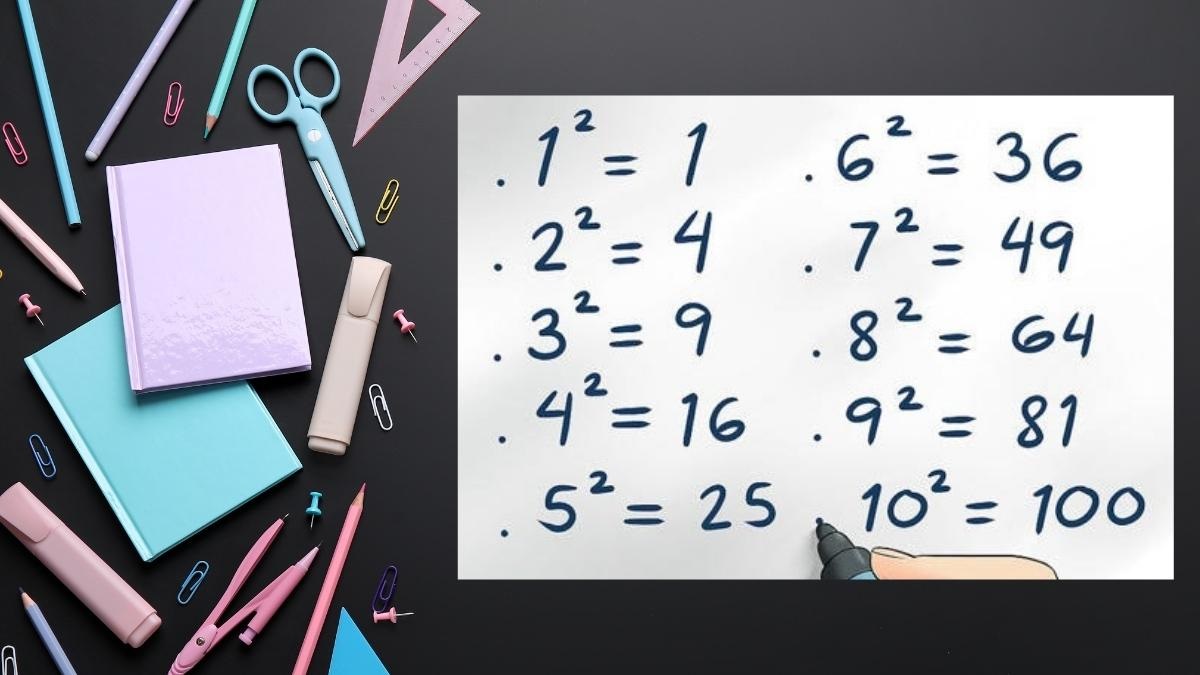
Định nghĩa về những con số

Nó là kết quả của việc nhân một số với chính nó. Cụ thể hơn, với một số nguyên n, bình phương của n là kết quả của việc nhân n với chính nó. Ký hiệu của n là n2 (phát âm là n bình phương). Ví dụ: bình phương của 3 là 3² = 3 × 3 = 9.

Nó có thể được biểu diễn dưới dạng một chuỗi các số liên tiếp bắt đầu từ 1.Cụ thể, dãy số vuông đầu tiên là 1, 4, 9, 16, 25, 36, 49, v.v.

Chúng có nhiều ứng dụng trong toán học và các lĩnh vực khác.Ví dụ, trong đại số, chúng thường được sử dụng trong phương trình bậc hai để giải các bài toán hình học và diện tích. Trong vật lý, chúng liên quan đến các khái niệm như diện tích, chiều dài và năng lượng.

Tính chất của số chính phương

Khi bạn đã biết được định nghĩa thì ta cần phải biết về những tính chất.Dưới đây là một số tính chất quan trọng của những con số:

Những con số có tính chất không âm

Tất cả các số đều không âm. Bởi vì một số là kết quả của việc nhân một số với chính nó,ví dụ các số như 0, 1, 4, 9, 16 đều không âm.

Những con số và căn bậc hai

Những con số cũng liên quan chặt chẽ đến khái niệm căn bậc hai.Ví dụ: căn bậc hai của một số là một số nguyên. Mặt khác, nếu một số có căn bậc hai là số nguyên thì số đó là số chính phương.

Cộng các số và bình phương

Khi cộng hai số,ta được một số khác. Ví dụ: 4 + 9 = 13 không phải là số nhưng 4 + 9 = 13 + 0 = 16 là số bình phương.

Dấu hiệu nhận biết số chính phương

Có một số dấu hiệu cho biết một số có phải là số bình phương hay không. Dưới đây là những dấu hiệu chính để nhận biết số:

Kiểm tra căn bậc hai

Chúng là số có căn bậc hai là số nguyên. Điều này có nghĩa là nếu căn bậc hai của một số là số nguyên thì số đó là số. Ví dụ, căn bậc hai của 9 là 3, là một số nguyên, nên 9 là số.

Kiểm tra hệ số nguyên tố

Một số có thể được chia thành tích của các thừa số nguyên tố lặp lại. Ví dụ: số chính phương hoàn hảo 25 có thể được chia thành 5 x 5, trong đó cả hai thừa số đều là 5. Nếu một số không thể chia thành các thừa số nguyên tố lặp lại thì đó không phải là số hoàn hảo.

Kiểm tra chữ số cuối cùng

Một số có thể có chữ số cuối cùng là 0, 1, 4, 5, 6 hoặc 9. Điều này liên quan đến cách một số bình phương được biểu diễn dưới dạng bình phương của một số nguyên.

Kiểm tra phép chia

Một số chia hết cho căn bậc hai của nó. Ví dụ: 16 là số và chia hết cho căn bậc hai của nó là 4.5.

Kiểm tra dãy số

Có thể kiểm tra một số xem nó có thuộc dãy số hay không. Dãy số phương là một dãy liên tục gồm các số chính phương hoàn hảo bắt đầu từ 1. Nếu một số nằm trong dãy số hoàn hảo thì đó là một số phương hoàn hảo.

Số chính phương là những số nào có chia hết cho 2 không?

Các số không chia hết cho 2 khi và chỉ khi chữ số tận cùng của chúng là 1, 4 hoặc 9. Các số có chữ số tận cùng là 0, 5 hoặc 6 thì chia hết cho 2. Vì vậy, cần tìm các số không chia hết cho 2 để có thể xét các số phương có chữ số tận cùng là 1, 4 hoặc 9. Ví dụ: 1, 4, 9, 16, 25, 36, 49, 81, 100, 121, 144, v.v.

Bài tập áp dụng

Bài tập 1:

Số nào sau đây chia hết cho 2?

a) 9

b) 16

c) 25

d) 36

Đáp án:

b) 16

Bài tập 2:

Số nào sau đây không chia hết cho 3?

a) 9

b) 16

c) 25

d) 36

Đáp án:

b) 16

Bài tập 3:

Số nào sau đây có chữ số cuối cùng là 1?

a) 9

b) 16

c) 25

d) 36

Đáp án:

a) 9

Bài tập 4:

Số nào sau đây là số nguyên tố?

a) 9

b) 16

c) 25

d) 37

Đáp án:

d) 37

Bài tập 5:

Số nào sau đây là số phương của một số nguyên dương khác?

a) 9

b) 16

c) 27

d) 36

Đáp án:

c) 27

Bài tập 6:

Số nào sau đây không chia hết cho 4?

a) 9

b) 16

c) 25

d) 36

Đáp án:

a) 9

Bài tập 7:

Số nào sau đây có tổng các chữ số cũng là số phương?

a) 9

b) 16

c) 25

d) 81

Đáp án:

d) 81

Tóm lại nếu bạn muốn tìm hiểu thêm về số phương, bạn có thể sử dụng tính chất, các phép toán liên quan và ứng dụng thực tế của chúng. Số bình phương là một phần quan trọng trong thế giới số học và việc nghiên cứu chúng sẽ giúp chúng ta hiểu rõ hơn về cấu trúc và tính chất của số nguyên.Hy vọng rằng việc tìm hiểu về số phương sẽ giúp bạn có cái nhìn tổng quan về khái niệm này và cho phép bạn áp dụng kiến thức này vào các vấn đề và bài toán trong thế giới thực.